Cart on an Air Track
Task number: 1750
A cart of mass of 250 g on an air track is being pulled and accelerated by a string over a fixed pulley. Compare the magnitude of acceleration in the following scenarios:
a) We pull the string with a force of 0.1 N.
b) We hang a weight of 0.1 N on the string.
Neglect the air resistance and the masses of the string and the pulley.
Note: An air track is a device that allows the cart to move without friction. The cart is suspended over the track with air jets

Notation
mv = 250 g mass of the car F = 0.1 N magnitude of the force applied to the cart by hand via the string FGw = 0.1 N magnitude of the force applied by the weight a1 = ? magnitude of the acceleration of the cart when pulled by a hand with a force of 0.1 N a2 = ? magnitude of the acceleration of the cart when pulled by the weight of 0,1 N Hint 1a – Forces Acting Upon the Cart, Equation of Motion
Draw a picture of the situation and include all the forces that act upon the cart if we are pulling on the string with a force of 0,1 N. Write down the equations of motion for the cart.
Hint 2a – Equation of Motion in Scalar Form
Write the equation of motion (1) in scalar form and find the magnitude of the acceleration a1.
Hint 1b – Forces Acting Upon the Cart and the Weight, Equations of Motion
Draw a picture of the situation and include all the forces that act upon the cart and the weight. Write the equation of motion for the cart and for the weight.
Hint 2b – Equations of Motion in Scalar Form, Tension Force of the String
Write the equations of motion (7) and (8) in scalar form. Remember what the relation between the tension forces T and T' of the string is.
Hint 3b – Calculating the Acceleration
Calculate the magnitude of the acceleration a2 using equations (10) and (11).
Note
The acceleration a1 is greater than a2. That is because in the first case the force of 0.1 N acts only upon the cart and it accelerates only the cart. In the seconds case the force of 0.1 N acts upon both the cart and the weight, so it has to accelerate both the cart and the weight.
COMPLETE SOLUTION
Forces acting upon the cart in situation a):
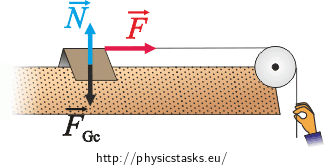
\(\vec{F}\)…force applied to the cart by hand via the string,
\(\vec{N}\)…force applied by the air suspending the cart from below,
\(\vec{F}_{G_c}\)…gravitational force acting upon the cart.
Equation of motion:
\[\vec{F}_{G_c}+\vec{N}+\vec{F}\,=\, m_c\vec{a_1},\tag{1}\]\(m_c\)…mass of the cart,
\(\vec{a}_1\)…acceleration of the cart.
To write the equation of motion in scalar form we first have to introduce an appropriate coordinate system. We choose the x axis in the direction of the motion of the cart, the y axis is perpendicular to the x axis.
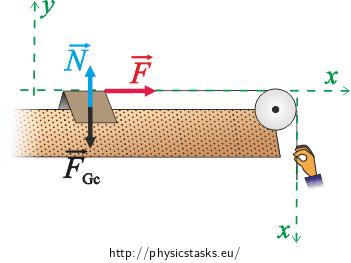
The equation of motion in scalar form:
\[x:\qquad F\,=\,m_c a_1,\tag{2}\] \[y:\qquad N - F_{G_c} \,=\,0.\tag{3}\]The cart doesn’t move in the direction of the y axis, its acceleration in this direction is therefore zero.
We calculate the magnitude of acceleration a1 from equation (2):
\[ a_1\,=\,\frac{F}{m_c}.\tag{4}\]Numerically:
\[ a_1\,=\,\frac{0.1}{0.25}\,\mathrm{m \cdot s^{-2}}\,=\, 0.4\,\mathrm{m \cdot s^{-2}}.\tag{5}\]Forces acting upon the cart and the weight in situation b):
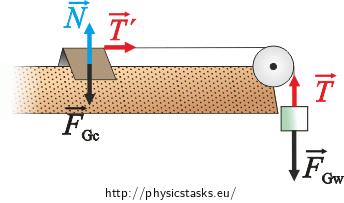
The cart:
\(\vec{N}\)…force applied by the air suspending the cart from below ,
\(\vec{F}_{G_c}\)…gravitational force acting upon the cart,
\(\vec{T}\prime\)…force applied to the cart by the weight via the string.
The weight:
\(\vec{F}_{G_w}\)…gravitational force acting upon the weight,
\(\vec{T}\)… force acting upon the weight by the cart via the string.
Equations of motion:
Equation of motion for the cart:
\[\vec{F}_{G_c}+\vec{N}+\vec{T}\prime\,=\, m_c\vec{a}_2.\tag{6}\]Equation of motion for the weight:
\[\vec{F}_{G_w}+\vec{T}\,=\,m_w\vec{a}_2,\tag{7}\]\(m_c\)…mass of the cart,
\(m_w\)…mass of the weight,
\(\vec{a}_2\)…the acceleration of the cart and the weight.
To write the equation of motion in scalar form we first have to introduce an appropriate coordinate system. We choose the x axis in the direction of the motion of the cart, the y axis is perpendicular to the x axis.
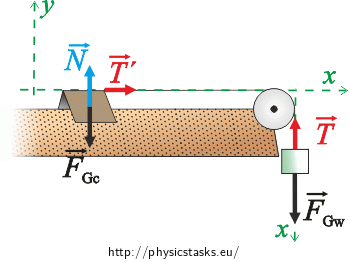
Equations of motion in scalar form:
Equation of motion for the cart:
\[x:\qquad T\prime\,=\,m_ca_2,\tag{8}\] \[y:\qquad N - F_{G_c}\,=\,0.\tag{9}\]The cart doesn’t move in the direction of the y axis, its acceleration in this direction is therefore zero.
Equation of motion for the weight:
\[x:\qquad F_{G_w}-T\,=\,m_wa_2.\tag{10}\]We are neglecting the mass of the pulley, therefore it has no moment of inertia and it doesn’t affect the tension force of the string. The cart acts upon the weight and the weight acts upon the cart. According to Newton’s Third Law of Motion it holds for the magnitudes of the tension forces that:
\[|\vec{T}| \,=\, |\vec{T}\prime|.\]We will rewrite equation (8):
\[T\,=\,m_ca_2.\tag{11}\]We will add equations (10) and (11) together:
\[F_{G_w}\,=\,m_wa_2+m_ca_2,\] \[F_{G_w}\,=\,\left(m_w+m_c\right)a_2,\] \[a_2\,=\,\frac{F_{G_w}}{m_w+m_c}.\]The mass of the weight is \(m_w\,=\,\frac{F_{G_w}}{g}\), therefore:
\[a_2\,=\,\frac{F_{G_w}}{\frac{F_{G_w}}{g}+m_c}.\tag{12}\]We substitute numerically into equation (12):
\[a_2\,=\,\frac{0{,}1}{\frac{0{,}1}{10}\,+\,0.25}\,\mathrm{m\cdot s^{-2}}\,=\, \frac{0.1}{0.26}\,\mathrm{m\cdot s^{-2}}\,=\,0.38\,\mathrm{m\cdot s^{-2}}.\tag{13}\]COMPLETE ANSWER
The magnitude of acceleration of the cart when we pull the string by hand with a force of 0.1 N is
\[a_1\,=\,\frac{F}{m_c}\,=\,0.4\,\mathrm{m\cdot s^{-2}}\,.\]The magnitude of acceleration of the cart when we hang a weight of 0.1 N on the string is
\[ a_2\,=\,\frac{F_{G_w}}{\frac{F_{G_w}}{g}+m_c}\,=\,0.38\,\mathrm{m\cdot s^{-2}}\,.\]Note: The acceleration a1 is greater than a2. That is because in the first case the force of 0.1 N acts only upon the cart and it accelerates only the cart. In the seconds case the force of 0.1 N acts upon both the cart and the weight, so it has to accelerate both the cart and the weight.




