Collection of Solved Problems in Physics

Measuring of the electrical conductivity of sea water

Task number: 1040

• I. Hints

• Hint 1

  Divide the space between the conductors into thin spherical surfaces with the radius r (a < r < b) and the thickness dr.

  

  The whole conductor is now a series connection of these surfaces and the total electrical resistance is equal to a sum of all resistances of each individual sphere.

• Hint 2

  Realize how the electrical resistance of one spherical shell can be calculated depending on the size and electrical conductivity.

• Solution of Hint 2

  Electrical resistance R of a homogenous conductor is inversely related to the electrical conductivity of the material.

  \[R\,=\,\frac{1}{\sigma}\frac{l}{S}\,,\]

  where l is a length of the conductor and S is an area of its cross-section.

  The whole conductor was divided into thin spherical shells with the radius r. The “area” of each sphere is equal to 4πr² and its “length” is called dr. The electrical resistance of each shell with radiuses r is:

  \[\mathrm{d}R\,=\,\frac{1}{\sigma}\frac{\mathrm{d}r}{4\pi r^2}\,.\]

• I. Analysis

  The space between conductors can be divided into thin spherical shells with radius r (a < r < b).

  

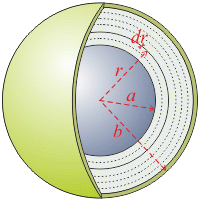
  The whole conductor can be now understood as a series connection of these shells. The total electrical resistance is equal to a summ (integral) of resistances of each individual shell.

  TThe electrical resistance of a spherical shell is directly related to its “length” and inversely related to the area of the shell and its electrical conductivity.

  The electric current flowing between the electrodes is equal to the ratio of voltage and electrical resistance between these electrodes.

• I. Solution

  The space between the electrodes can be divided into thin shells with the radiuses r (a < r < b) and the “thickness” dr.

  

  The electrical resistance of the spherical shell can be calculated from the equation:

  \[R\,=\,\frac{1}{\sigma}\frac{l}{S}\,,\]

  where σ is electrical conductivity of the material, l is the length of the conductor and S is the area of the conductor cross-section.

  In this case, the “area” of the spherical shell is equal to the area of the spherical surface, i.e. 4πr². Let’s mark the “length” of the shell dr. The electrical resistance dR of the shell with the radius r can be expressed by the formula:

  \[\mathrm{d}R\,=\,\frac{1}{\sigma}\frac{\mathrm{d}r}{4\pi r^2}\,.\]

  The individual shells are connected in series. The total electrical resistance between the spherical electrodes is equal to the sum (integral) of the electrical resistance dR of all shells. Limits of the integration are the radiuses a and b.

  \[ R\,=\,\int_a^b\,\frac{1}{\sigma}\,\frac{\mathrm{d}r}{4\pi r^2}\,=\, \frac{1}{4\pi \sigma}\int_a^b\frac{\mathrm{d}r}{r^2}\,=\,\frac{1}{4\pi \sigma}\,\left[-\frac{1}{r}\right]_a^b \,. \]

  The total electrical resistance between the spherical electrodes can be calculate as:

  \[R\,=\,\frac{1}{4\pi \sigma}\left(\frac{1}{a}\,-\,\frac{1}{b}\right)\] \[R\,=\, \frac{1}{4\pi \sigma}\,\frac{b\,-\,a}{ab}\] \[R\,=\,\frac{b\,-\,a}{4\pi \sigma ab}\,.\]

  The electric current flowing between the electrodes is equal to the ratio of the voltage U and the electrical resistance R between the electrodes:

  \[I\,=\,\frac{U}{R}\,=\,\frac{4\pi \sigma ab}{ b\,-\,a}\,.\]

• II. Hints

• Hint 1

  Find the formula for the Ohm’s law in the differential form.

• Solution of Hint 1

  The formula for the Ohm’s law in the differential form is:

  \[ \vec{j\,}=\,\sigma \vec{E}\,, \]

  where \(\vec{j\,}\) means a current density, σ is a material dependent parameter called conductivity and \(\vec{E}\) is the electric field at a given location.

• Hint 2

  Determine the magnitude of the voltage between the spherical electrodes using the electric field.

  The total electrical resistance of the conductor is equal to the ratio of voltage and the total electric current flowing between the electrodes.

• Solution of Hint 2

  Electrical voltage U arises between the ends of the conductor due to the electric field. This voltage is equal to the difference of electric potentials of the both ends.

  The relation between the electric field \(\vec{E}\) and the potential \(\varphi\) in the point P is:

  \[ \varphi =-\int_0^P \vec{E}\cdot\mathrm{d}\vec{r\,}, \]

  where we integrate from the point with a zero potential to the point P (the integral is independent of the path taken).

  The voltage between two concentric spherical electrodes with radiuses a and b (a < b) is equal to the difference of the electric potentials in these points:

  \[ U\,=\,\varphi_{(a)}\,-\,\varphi_{(b)}\,=\,-\int_0^a\vec{E}\cdot\mathrm{d}\vec{r\,}\,+\,\int_0^b\vec{E}\cdot\mathrm{d}\vec{r\,} \] \[ U\,=\,\int_0^b\vec{E}\cdot\mathrm{d}\vec{r\,}\,-\,\int_0^a\vec{E}\cdot\mathrm{d}\vec{r\,}\,=\, \int_a^b \vec{E}\cdot\mathrm{d}\vec{r\,} \]

• II. Analysis

  The space between spherical conductors can be divided into thin spherical shells with the radiuses r, where a < r < b

  

  It follows from the spherical symmetry that the electric density is equivalent in all points of such a formed shell. The electric density can be expressed using the total current and the surface of the shell. The total current between electrodes is constant and independent of the radius r.

  The Ohm’s law in the differential form for homogenous conductors says that the density of current flowing through the conductor is equal to the product of electrical conductivity and the electric field of the conductor. We can express the electric field from this law

  We gain the electrical voltage between the electrodes by the integration of the electric field. The total electrical resistance of the material can be determined as a ratio of the electrical voltage and the electric current flowing between the electrodes.

• II. Solution

  The space between spherical conductors can be divided into thin spherical shells with the radiuses r, where a < r < b. From the spherical symmetry it follows that the current density j is equivalent in all points of such a shell. The total current flowing through the shell can be calculated as:

  \[ I=S\,j\left(r\right)=4\pi r^2\,j\left(r\right)\,. \]

  The total electric current is constant and therefore it is independent of the radius r.

  The differential form of Ohm’s law for a homogenous conductor says:

  \[ \vec{j\,}=\,\sigma\vec{E}, \]

  where σ means an electrical conductivity and \(\vec{E}\) is an electric field. Now we can determine the size of the electric field in the spherical shell with the radius r:

  \[ E\left(r\right)\,=\,\frac{j\left(r\right)}{\sigma} \]

  Just as the current density j(r) so the magnitude of the electric field E(r) depends on the radius of the shell r. The current density j(r) in a spherical conductor with the radius r can be calculated from the equation for the total current.

  \[ E\left(r\right)\,=\,\frac{I}{4\pi r^2\sigma} \]

  The electrical voltage U between the electrodes can be determined by integration of the electric field:

  \[ U\,=\,\int_a^b \vec{E}\left(r\right)\cdot \mathrm{d}\vec{r\,} \]

  Thanks to the spherical symmetry, the electric field will point in the radial direction at each point of the conductor. Therefore, the vectors \(\vec{E}\) and d\(\vec{r}\) are parallel and their scalar product is equal to the product of their amplitudes:

  \[ U\,=\,\int_a^b E\left(r\right)\,\mathrm{d}r\,=\,\frac{I}{4\pi \sigma}\int_a^b \frac{\mathrm{d}r}{r^2}\,=\,\frac{I}{4\pi \sigma}\,\left[\frac{-1}{r}\right]_a^b\,=\,\frac{I}{4\pi \sigma}\,\left(\frac{1}{a}\,-\,\frac{1}{b}\right) \]

  The electrical resistance can be calculated as a ratio of the electrical voltage and the electric current flowing between the electrodes:

  \[ R\,=\,\frac{U}{I}\,=\,\frac{\frac{I}{4\pi \sigma}\,\left(\frac{1}{a}\,-\,\frac{1}{b}\right)}{I} \]

  The total electrical resistance between the two electrodes can be determined from the equation:

  \[ R\,=\,\frac{1}{4\pi\sigma}\left(\frac{1}{a}\,-\,\frac{1}{b}\right) \] \[ R\,=\,\frac{1}{4\pi\sigma}\,\frac{b-a}{ab} \] \[ R\,=\,\frac{b-a}{4\pi\sigma ab} \]

  The electric current flowing between the electrodes is equal to the ratio of the electrical voltage and the electrical resistance between the electrodes:

  \[ I\,=\,\frac{U}{R}\,=\,\frac{4\pi\sigma ab}{b-a}\,U \]

• III. Hints

• Hint 1

  The electric field created between the spherical electrodes is constant in time (it is stationary). In the stationary situation we can use a formal analogy with the electrostatic laws.

• Hint 2

  Realize or find the equation for the Gauss‘s law of electrostatics in the integral form.

• Solution of Hint 2

  The Gauss‘s law in the integral form is:

  \[ \oint \vec{E}\cdot \mathrm{d}\vec{S}\,=\,\frac{Q}{\epsilon} \]

  The symbol \(\oint\) means that the planar integral is calculated across a closed area, the symbol \(\vec{E}\) is the electric field, Q is the total electric charge closed in the area S and ε is the permittivity of the given material.

  The Gauss‘s law gives the relation between electric field and the electric charge.

• Hint 3

  If there was a dielectric instead of a conductor between the electrodes, the whole setup would be actually a capacitor. Thanks to the formal analogy with the electrostatic laws, the course of the electric field is the same. The electric field in the Gauss’s law can then be expressed in the stationary form, but for the electric charge Q we borrow the equation from the static case.

  Therefore, the size of the electric charge can be expressed using a capacity of spherical electrodes. Such an expressed size of the charge can be substituted for the Gauss’s law in electrostatics.

• Solution of Hint 3

  The relation between electric charge Q and the difference in electric potentials U can be expressed using the capacity C of the spherical electrodes:

  \[ Q\,=\,CU \]

  The capacity C is given by the relation:

  \[ C\,=\,\frac{4\pi \epsilon}{\frac{1}{a}\,-\,\frac{1}{b}}\,=\,\frac{4\pi\epsilon}{\frac{b-a}{ab}} \] \[ C\,=\,\frac{4\pi\epsilon ab}{b-a} \]

  where ε means the electric permittivity of the surroundings and a, b are radiuses of the spherical areas creating the capacitor (a < b).

• Hint 4

  Realize how the Ohm’s law in the differential form looks like.

  Note: The Ohm’s law in the differential form can be found in this task in section II. Hint 1.

• III. Analysis

  The electrical resistance and the electric current flowing between two spherical electrodes can be calculated using the formal analogy with the electrostatics field.

  Consider similar electrodes submerged into a dielectric with a definite electric permittivity. The electric charges of the same size but opposite signs are brought to the electrodes. These electrodes keep the original values of potentials. Therefore, the equal course of the electric field will be between the electrodes. The Gauss’s law in the integral form can be used for expressing the electric field.

  The Ohm’s law for a homogenous conductor in differential form can be substituted for the equation of the electric field. This way, we gain the electric current flowing between the electrodes depending on the size of the electric charge of the spherical electrodes. Therefore, the electric charge can be expressed using the capacity of a spherical capacitor.

  According to the Ohm’s law, the electrical resistance between the spherical electrodes is equal to the ratio of voltage between the electrodes and the electric current flowing between them.

• III. Solution

  Let’s imagine that a dielectric with a permittivity ε is put between the electrodes, and charges with the same quantity Q but opposite signs are brought to the electrodes. The charges keep original value of the electric potentials. To solve the task, we can use the fact that the course of the electric field is the same as in this stationary case, when a steady electric current flows between the electrodes.

  At first we write two equations describing the spherical capacitor that we will use later. The interrelation between the size of a charge Q, a potential difference (i.e. voltage U), and a capacity C can be expressed by an equation:

  \[ Q\,=\,UC \]

  The capacity of the spherical capacitor is:

  \[ C\,=\,\frac{4\pi\epsilon}{\frac{1}{a}\,-\,\frac{1}{b}}\,=\,\frac{4\pi\epsilon ab}{b-a}\,, \tag{*}\]

  where ε means a permittivity of the environment, and a, b (a < b) are radiuses of the spherical electrodes creating the capacitor.

  Let’s assail the very solution of the task. We apply the integral form of the Gauss’s law:

  \[ \oint \vec{E}\cdot\mathrm{d}\vec{S}\,=\,\frac{Q}{\epsilon}\,, \]

  where \(\vec{E}\) means an electric field , Q is a charge brought to the spherical electrodes with a surface S, and ε means a permittivity of the stated material.

  The formula for the Ohm’s law for a homogeneous conductor in the differential form is:

  \[ \vec{j}\,=\,\sigma \vec{E} \]

  where \(\vec{j}\) is a current density, and σ is a material dependent parameter called conductivity.

  The total electric current I flowing through the electrodes can be expressed by using the current density  \(\vec{j}\):

  \[ I\,=\,\oint \vec{j\,}\cdot\mathrm{d}\vec{S}, \]

  where the current density \(\vec{j\,}\) can be substituted from the Ohm’s law. Further, we use the Gauss’s law for the modification of the equation:

  \[ I\,=\,\oint \sigma \vec{E}\cdot\mathrm{d}\vec{S}\,=\,\sigma\oint\vec{E}\cdot\mathrm{d}\vec{S}\,=\,\sigma\frac{Q}{\epsilon} \]

  The electric charge Q placed on one electrode can be expressed by using the capacity: \(Q\,=\,CU\); i.e.:

  \[ I\,=\,\sigma\frac{CU}{\epsilon} \]

  We gain an equation for computation of the total electric current flowing through the electrodes thanks to the substitution of the capacity of the spherical capacitor (*) for C.

  \[ I\,=\,\sigma\frac{\frac{4\pi\epsilon ab U}{b-a}}{\epsilon} \] \[ I\,=\,\frac{4\pi\sigma ab}{b-a}\,U \]

  The electrical resistance between the spherical electrodes can be calculated as a ratio of the voltage U between the electrodes and the electric current I flowing between the electrodes:

  \[ R\,=\,\frac{U}{I}\,=\,\frac{U}{\frac{4\pi\sigma ab}{b-a}\,U} \] \[ R\,=\,\frac{b-a}{4\pi\sigma ab} \]

• b) Hints

• Hint 1

  We calculated the electrical resistance between two spherical conductors with radiuses a and b (a < b) in the previous parts of the task:

  \[ R\,=\,\frac{b-a}{4\pi\sigma ab}\,=\,\frac{1}{4\pi\sigma}\left(\frac{1}{a}\,-\,\frac{1}{b}\right). \]

  Realize, how the resistance will change, if the radius b of the external conductor is many times bigger than the radius a of the inner sphere (i.e. b >> a).

• Solution of Hint 1

  If the radius b of the external conductor is many times bigger than the radius a of the inner sphere (i.e. b >> a), then the reciprocal of the radius b is many times smaller than the reciprocal of the radius a, thus \[\frac{1}{b}\,<<\,\frac{1}{a}.\]

  The resistance of the environment between the two spherical conductors can be calculated from the equation:

  \[ R\,=\,\frac{1}{4\pi\sigma}\left(\frac{1}{a}\,-\,\frac{1}{b}\right). \]

  If b >> a, then the term \(\frac{1}{b}\) can be neglected. This way, we gain an equation for the resistance of the environment:

  \[ R\,\approx\,\frac{1}{4\pi\sigma a} \]

  For this reason, the matter that is concentrated close to the surface of the sphere with the radius a contributes the most to the resistance of the environment. This equation can be considered in first explanation to be the resistance of the surroundings of the spherical electrode with the radius a.

• Hint 2

  In order to calculate the electric current flowing between two spherical electrodes that are submerged deep in the sea and are located in a considerable distance, it is necessary to determine the electrical resistance of the water between them. We know from Hint 1 that the matter concentrated closely to the electrode contributes the most to the resistance. We also know how to calculate it. The resistance of the water between both electrodes can be thus calculated as a resistance of two “surroundings of electrodes” connected in series.

• b) Analysis

  Let’s suppose we have two concentric spherical metal conductors with radiuses a and b (a << b). Thanks to this condition, we gain an equation for the electrical resistance of the surroundings of the spherical electrode with the radius a from the previous results.

  Therefore, the electric current flowing between two spherical electrodes that are submerged deep in the sea and are located in a considerable distance will be equal to the electric current flowing through two resistors connected in a series with resistances corresponding to the resistances of the surroundings of both electrodes.

• b) Solution

  We have calculated the electrical resistance between the two concentric spherical electrodes with the radiuses a and b (a < b) in the previous parts of the solution:

  \[ R\,=\,\frac{b-a}{4\pi\sigma ab}\,=\,\frac{1}{4\pi\sigma}\left(\frac{1}{a}\,-\,\frac{1}{b}\right), \tag{*}\]

  where σ is the electrical conductivity of the material, i.e. of the sea water in this case.

  If b >> a, then \[\frac{1}{b}\,<<\,\frac{1}{a}\] . Which means that the term \[\frac{1}{b}\] in the equation (*) can be neglected. Therefore, the equation for the electric resistivity of the environment is:

  \[ R\,\approx\,\frac{1}{4\pi\sigma a} \]

  The resistance of the environment is concentrated mostly near the surface of the sphere. Therefore, this equation can be considered in first approximation to give the resistance of the surroundings of the spherical electrode with the radius a.

  The electric current flowing between two spherical electrodes that are submerged deep in the sea and are located in a considerable distance will be equal to the electric current flowing through two resistors connected in a series with resistances corresponding to the resistances of the surroundings of stated electrodes. The total resistance of this series connection will be equal to the sum of these resistances:

  \[ R_{total}\,=\,2R\,\approx\,2\,\frac{1}{4\pi\sigma a}\,=\,\frac{1}{2\pi\sigma a} \]

  The electric current flowing between the spherical electrodes can be calculated as a ratio of the voltage U between the electrodes and the total resistance of the electrodes R_total; i.e.:

  \[ I\,\approx\,\frac{U}{R_{total}}\,=\,\frac{U}{\frac{1}{2\pi\sigma a}} \] \[ I\,\approx\,2\pi\sigma aU \]

• Answer

  a) The electrical resistance between the two concentric spherical electrodes with the radiuses a and b can be calculated from the equation:

  \[ R\,=\,\frac{b-a}{4\pi\sigma ab}. \]

  The electric current flowing between the electrodes is equal to:

  \[ I\,=\,\frac{4\pi\sigma ab}{b-a}\,U, \]

  where σ is the electrical conductivity of the material and U means the voltage between the electrodes.

  Note: All the three methods led to the same result.

  b) The electric current flowing between two spherical electrodes with the radius a that are dipped deep in the sea is:

  \[ I\,=\,2\pi\sigma aU. \]