How to connect capacitors
Task number: 301
There are enough capacitors of capacitance 2 µF. Each capacitor can be used with voltage up to 200 V without damage. How to connect them to a system of capacitors of total capacitance
a) 0.4 µF
b) 1.2 µF,
if each of these systems should be able to be connected to voltage up to 1 000 V without damage?
Hint: Capacitance of capacitors
Total capacitance is lower than capacitance of each one capacitor used therefore let’s connect capacitors in series.
When capacitors are connected in series, total capacitance is the reciprocal value of sum of reciprocal values of several capacitances:
\[\frac{1}{C}\,=\,\frac{1}{C_1}+\frac{1}{C_2}+\dots+\frac{1}{C_N}\]When capacitors are connected in parallel, total capacitance is the sum of several capacitances:
\[C\,=\,C_1+C_2+\dots C_N\]Hint: Voltage on capacitors
When connected in series, total voltage is a sum of voltage on each capacitor.
\[U\,=\,U_1+U_2+\dots +U_N\]In parallel circuit is voltage on each capacitor the same as the total voltage.
\[U\,=\,U_1\,=\,U_2\,=\,\dots\,=\,U_N\]Hint: How to get capacitance 1.2 µF
When solving this objective, let us use the result of the part a).
Is it possible to get capacitance 1.2 µF using some 0.4 µF capacitors?
Hint: How to get capacitance 0.4 µF
Total capacitance is lower than capacitance of several capacitors. Let’s connect the capacitors in series.
Analysis
There is no universal method of solving this kind of tasks successfully but we can use some hints.
Whenever we connect capacitors in parallel, we get higher total capacitance than the capacitance of connected capacitor.
On the contrary when we connect capacitors in series, we always get lower total capacitance than capacitance of each capacitor.
In this task we have to get total capacitance lower than the capacitance of the connected capacitors, therefore we have to connect at least some of the capacitors in series.
Note, that we can get the capacitance 1.2 µF by connecting capacitors with capacitance 0.4 µF. The second part of the task we can solve using the result of the first part (we can imagine, that we are connecting several capacitors with capacitance 0.4 µF).
a) Solution: How to get capacitance 0.4 µF
We want to get total capacitance lower than the capacitance of each capacitor used so we have to connect them in series. (When connected in parallel total capacity is the sum of particular capacitances and therefore we cannot obtain requested lower capacitance this way.)
First we have to enumerate number of capacitors to connect in series to obtain capacitance 0.4 µF. Afterwards we will have to ensure, that this system can be connected to voltage 1000 V without any damage.
When the same capacitors (each with capacitance C) are connected in series:
\[\frac{1}{C_c}\,=\, \frac{1}{C}+\frac{1}{C}+\frac{1}{C}+\dots\frac{1}{C}\]Number of fractions on the right side of the equation is equal to the number of capacitors connected in series. Let’s simplify it – for x capacitors in series we can write it this way:
\[\frac{1}{C_c}\,=\, \frac{x}{C}\] Evaluate number of capacitors x from that equation. \[x\,=\, \frac{C}{C_c}\]Numerically:
\[x\,=\, \frac{2 \,\mathrm{\mu F}}{0.4\, \mathrm{\mu F}}\,=\,5\]To obtain total capacitance 0.4 µF we have to connect 5 capacitors each with capacitance 2 µF in series.
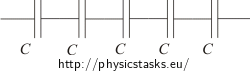
Now we have to check whether we can connect this system to the voltage 1 000 V without any damage.
Each capacitor can be connected to a voltage 200 V. When capacitors are connected in series, total voltage is the sum of voltages on particular capacitors. When connected 5 same capacitorsin series, maximal total voltage can be \[U_c\,=\,5U\,=\,5{\cdot}200\,\mathrm{V}\,=\,1\,000\,\mathrm{V}\] .
The system can be connected to the voltage 1 000 V without damage.
Note: 5 capacitors is the lowest number of capacitors that can be connected in series and use without damage when connected to the voltage 1 000 V
b) Solution: How to get capacitance 1.2µF
Capacitance 1.2 µF is lower than the capacity of each capacitor we have. In this case we can not connect the capacitors in series because we should connect less than 5 capacitors to get requested capacitance and so the voltage on particular capacitors would be too high. Therefore we have to do something different.
Note that the capacitance 1.2 µF is three times bigger than the 0.4 µF capacitance we got as a solution in the first part of this task. So we can imagine that we have capacitors with capacitance 0.4 µF (each composed by 5 real capacitors connected in series as realised in the first part of the task) and we can combine them to get requested capacitance 1.2 µF.
The question is how many of these “capacitors” we have to use. The capacitance 1.2 µF is higher than capacitance of each “capacitor” having 0.4 µF, so we have to connect them in parallel (in this case total capacitance is a sum of capacities of several capacitors).
\[C_c\,=\,C+C+\dots+C\]To get capacitance 1.2 µF we have to connect 3 capacitors with capacitance 0.4 µF in parallel.
\[C_c\,=\,3C\] \[1.2\,=\,3{\cdot} 0.4\]Now we have to substitute back each 0.4 µF “capacitor” with five 2 µF.
We have got three groups connected in parallel, each composed with 5 capacitors connected in series.
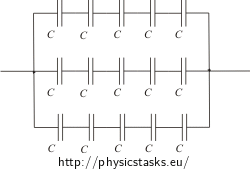
The question is whether the system can be connected to 1 000 V power supply without any damage. When some objects are connected in parallel, the voltages on all these objects are the same. In the first part of the task we have calculated, that each branch (composed by five capacitors connected in series) can be connected to such voltage without any damage so all the system can be connected to the power supply too.
Answer
To get capacitance 0.4 µF we have to connect five 2 µF capacitors in series.
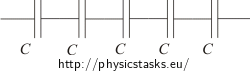
To get total capacity 1.2 µF we have to connect three groups of capacitors in parallel, each composed of five 2 µF capacitors in series.

What to do if there is damage risk because of too high voltage
What can we do, when the system of connected capacitors have requested total capacitance, but the voltage is too high and there is a risk of damage?
In that case we have to connect more capacitors in series. But by this step we also reduced the total capacity of the system so we have to connect another capacitors in parallel to increase the total capacity.
Example: What we have to do, when our system have to be connected to 2 000 V power supply without any damage?
We have connected 5 capacitors in series. The total capacitance is 0.4 µF and the system can be connected to 1 000 V. What do we have to change to be able to connect the system to 2 000 V?
If the system should be connected to 2 times higher voltage, we have to connect two times more capacitors (10) in series. By this step we reduced the total capacitance to one half, to get i back we have to connect the same system (another 10 capacitors with the same parameters) one more time in parallel to this one. Now total capacitance of the whole system is 0.4 µF and it can be connected to 2 000 V power supply without any damage.



