Circuit with a switch

Task number: 661

The generator in the picture is a source of alternating voltage 230 V with frequency 50 Hz. There is one coil, two same capacitors and a resistor connected to the circuit. All of them have an unknown value of impedance. If we disconnect the switch (as shown in the picture) voltage lags behind current of the generator by 20°. If the switch is in the position 1, voltage overtakes a current of the generator by 10°. If the switch is in position 2, the current in the circuit is 2 A.

Find resistance of the resistor, inductance of the coil and capacity of the capacitor.

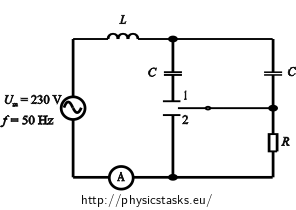
Notation

From the assignment we know:

Voltage of the generator:	U_m = 230 V
Frequency of the voltage:	f = 50 Hz
Disconnected switch:	voltage lags behind the current by φ₁ = -20°.
Switch in position 1:	voltage overtakes the current by φ₂ = 10°.
Switch in position 2:	the current in the circuit is I = 2 A.

We should find out:

Resistance of the resistor:	R = ? (Ω)
Inductance of the coil:	L = ? (H)
Capacity of the capacitor:	C = ? (F)

Hint
Examine the image of circuit. Focus primarily on, how the current flows through the circuit in each individual position of the switch. Redraw individual cases and omit the parts of the circuit, through which the current doesn´t flow.
Analysis
We know from assignment three characteristics of the circuit for three different positions of the switch. We should also find three unknown quantities. That means that we should change each assigned fact to equation, so that we gain a system of equations, where the unknown quantities are resistance of the resistor, capacity of the capacitor and inductance of the coil.

We redraw the assigned circuit into separate sections according to the position of the switch. In these circuits we will draw only the part of the circuit, in which the current flows. We will omit those parts, in which the current doesn´t flow.

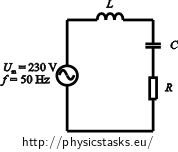
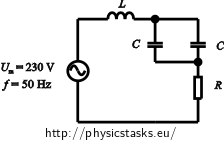
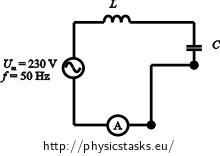
We use Ohm’s law to formulate phase shifts between voltage and current for the disconnected switch and for the switch in position 1. We formulate also value of impedance which is made (with switch in position 2) only from inductive reactance and capacitive reactance.

We gain three equations (one from each circuit) for three unknown values — capacitive reactance, inductive reactance and resistance. We will solve this system of equations and we will calculate the value of the capacity, inductance and resistance from the values we have gained.
Solution using a drawn circuit
Circuit with a disconnected switch:

For the phase shift in this case is true:
\[tg {\varphi}_1 = \frac{X_L-X_C}{R}\tag{1}\]
The phase shift between voltage and current is negative because voltage lags behind the current.

Circuit with switch in position 1:

The total capacity in this circuit is:
\[C_{p}=C+C\]
So, the total capacitive reactance has a form:
\[X_{C_{p}}=\frac{1}{4\pi f C}=\frac{1}{2}X_C\]
The value of the capacity reactance is half in this case unlike in the case with the disconnected switch because here are two parallel capacitors with the same capacity in the circuit with switch in position 1.

For the phase shift in this case is true:
\[tg {\varphi}_2 =\frac{X_L-\frac{1}{2}X_C}{R}\tag{2}\]
Phase shift is positive because voltage overtake current.

Circuit with the switch in position 2:

There isn’t any current flowing through the resistor. We know the current flowing through the ammeter. So, we can calculate the total impedance Z, which consists from inductive reactance and capacitive reactance.
\[Z=|X_L-X_C|=\frac{U_m}{I}\tag{3}\]
Solving the system of equations
We gain a system of three equations from the redrawn circuit in the previous section. Realize that impedance is in Ohm and we won’t write them into equations.

From the circuit with a disconnected switch:
\[ \frac{X_L-X_C}{R}=tg {\varphi}_1 =tg (-20^{\circ}) \dot=-0.364\tag{1}\]
From the circuit with a switch in position 1:
\[\frac{X_L-\frac{1}{2}X_C}{R}=tg {\varphi}_2 =tg (10^{\circ}) \dot=0.18\tag{2}\]
From the circuit with a switch in position 2:
\[|X_L-X_C|=\frac{U_m}{I}=\frac{230}{2} = 115 \tag{3}\]
We put equation (3) to equation (1) and express the resistance. We can „delete“ the absolute value in difference |X_L - X_C| because resistance R is positive. It is true that:
\[X_L-X_C=-115\]
Put it in the equation (1):
\[ \frac{X_L-X_C}{R}=tg {\varphi}_2 \] \[\frac{-115}{R}\dot=-0.364\] \[R\dot= 316\]
Now we have modified the task so that we get a system of two equations with two unknowns. Equations are modified from equations (1) and (2), in which we put calculated value of resistance R.
\[X_L-X_C=-115\tag{1}\] \[X_L-\frac{1}{2}X_C=0.18R\dot=56.88\tag{2}\]
We express from the first of them:
\[X_L=-115+X_C\]
and put it into the second one:
\[-115+X_C-\frac{1}{2}X_C\dot=56.88\]
so we gain:
\[X_C\dot=2(56.88+115)\dot=344\] \[X_L\dot=-115+344\dot=229\]

The value of resistance of the resistor, capacity of the capacitor and inductance of the coil (with units):
- Resistance of the resistor: \[R\dot= 316\,\mathrm \Omega\]
- Capacity of the capacitor: \[X_C=\frac{1}{2 \pi f C}\] \[C=\frac{1}{2 \pi f X_C}\dot=\frac{1}{ 2 \cdot \pi \cdot 50 {\cdot} 344}\,\mathrm F\] \[C\dot=9.3 \,\mathrm{\mu F}\]
- Inductance of the coil: \[X_L= 2 \pi f L\] \[L=\frac{X_L}{2 \pi f}\dot=\frac{229}{2\cdot \pi \cdot 50}\,\mathrm H\] \[L\dot=0.73\,\mathrm H\]
Answer
Resistance of the resistor in the circuit is approximately: R = 316 Ω.

Inductance of the coil in the circuit has a value approximately: L = 0.73 H.

Capacity of the capacitors in the circuit is approximately: C = 9.3 µF.

Difficulty level: Level 3 – Advanced upper secondary level