Current with Triangular Waveform
Task number: 1783
A current flowing through a 100 Ω resistor has a periodic triangular wave form. Asses:
- the average value of the current,
- the average dissipated power.
- the effective value of the current,
Compare to the values for a harmonic current with the same amplitude.
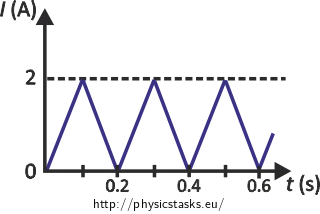
Hint for part a) - Definition of Average Current
The average value of the current in defined by the integral:
\[\bar{I}=\frac{1}{T} \int_{0}^{T}{i(t)}\,dt\]Let us draw a period-long rectangle whose area is equal to the area under one period of the waveform i(t) of the given (triangular) current. The height of such rectangle corresponds to the average value of the given current.
a) Solution - Average Current

The given current is periodic. We see in the graph that, within one period, the current has a symmetrical waveform. This means that the area under the graph in the first half-period is the same as the area under the graph in the second half-period. For this reason, we can rewrive the definition of the average current as follows. The integral over the whole period of a symmetrical waveform is equal to twice the integral over one half of the period:
\[\bar{I}=\frac{1}{T} \int_{0}^{T}{i\left(t\right)}\,dt=2\, \frac{1}{T} \int_{0}^{\frac{T}{2}}{i\left(t\right)}\,dt.\]The dependence of current on time - i(t) - is a linear function of time t in the first half-period:
\[i\left(t\right)=\frac{I_{\mathrm{max}}}{\frac{T}{2}}\,t= \frac{2\,I_{\mathrm{max}}}{T}\,t,\]where Imax is the maximal value of the current (as indicated by the dashed line in the Figure) and the slope of the line is (2Imax)/T, because the current reaches the maximum at time T/2.
Let us substitute to the integral for the average current:
\[\bar{I}=\frac{2}{T} \int_{0}^{\frac{T}{2}}{\frac{2\,I_{\mathrm{max}}}{T}\,t}\,dt=\frac{4\,I_{\mathrm{max}}}{T^2} \int_{0}^{\frac{T}{2}}\,t\,dt,\]and calculate the definite integral:
\[\bar{I}=\frac{4\,I_{\mathrm{max}}}{T^2} \int_{0}^{\frac{T}{2}}\,t\,dt=\frac{4\,I_{\mathrm{max}}}{T^2} \left[\frac{t^2}{2}\right]_0^{\frac{T}{2}}=\frac{4\,I_{\mathrm{max}}}{T^2}\, \left[\frac{\left({\frac{T}{2}}\right)^2}{2} - 0 \right]=\frac{I_{\mathrm{max}}}{2}.\]The average current is thus equal to one half of the maximum current.
trojuhelnik_EN.page.tagged.gif)
Note.: We wrote in the hint of the definition that the average current is given by the height of a period-long rectangle whose area is equal to the area under the waveform of one period of the alternating current. The validity of this statement is shown in the following figure.
trojuhelnik_EN.page.tagged.gif)
Hint for part b)
The relation between the maximal current and the average power for a triangular (= sawtooth) current is different than the ratio for a sinusoidal current.
We asses the relation by using the definition of the average power.
b) Solution - Average Power
The average Joule heating in a circuit with periodic alternating current is calculated similar to the average current: as an integral of the instantaneous Joule heating vi over the full period divided by the duration of the period:
\[\bar{P}=\frac{1}{T}\int_{0}^{T}{vi}\,\mathrm{d}t.\]Having only a resistor connected in the circuit, we can substitute the voltage v with the product of the current and the resistance of the resistor according to Ohm’s law:
\[\bar{P}=\frac{1}{T}\int_{0}^{T}{Ri^2}\,\mathrm{d}t.\]
The current has a symmetrical wave (the part of the current waveform in the first half-period is symmetric to the part in the second half-period). Thus we can rewrite the integral of Joule heating over the whole period to twice the integral over the first period:
\[\bar{P}=\frac{1}{T}\int_{0}^{T}{Ri^2}\,\mathrm{d}t=\frac{2}{T}\int_{0}^{T/2}{Ri^2}\,\mathrm{d}t.\]We express the current in the first half-period in the same way as in the solution of task a):
\[i=\frac{2\,I_{\mathrm{max}}}{T} t\]and substitute into the expression for Joule heating:
\[\bar{P}=\frac{2}{T}\int_{0}^{\frac{T}{2}}{R\left(\frac{2\,I_{\mathrm{max}}}{T} t\right)^2}\,\mathrm{d}t.\]The quadratic function is integrated as follows:
\[\int_{0}^{\frac{T}{2}}{R\left(\frac{2\,I_{\mathrm{max}}}{T} t\right)^2}\,\mathrm{d}t={\frac{4RI_{\mathrm{max}}^2}{T^2}}\int_{0}^{\frac{T}{2}}t^2\,\mathrm{d}t=\frac{4RI_{\mathrm{max}}^2}{T^2}\,\left[\frac{t^3}{3}\right]_0^{\frac{T}{2}}=\frac{4RI_{\mathrm{max}}^2}{T^2}\,\frac{\left({\frac{T}{2}}\right)^3}{3}=\frac{1}{6}\,RI_{\mathrm{max}}^2 T\tag{1}\]And the average Joule heating is:
\[\bar{P}=\frac{2}{T}\frac{1}{6}\,RI_{\mathrm{max}}^2 T=\frac{1}{3}\,RI_{\mathrm{max}}^2.\]Hint for part c)
The effective current is defined as the direct current that would yield the same average power as the given alternating current. Use this information and the solution of the previous two parts of the task to find the relation between the effective and the maximum current.
b) Solution - Effective Value of Current
The effective current Ieff and the effective voltage Veff are defined so that they yield the average Joule heating:
\[\bar{P}= V_{eff}\,I_{eff}\,.\]The phase shift between the voltage and the current is zero in our circuit because there is only a resistor connected in it. We use Ohm’s law to substitute the effective voltage with the effective current and the resistance of the resistor in the formula for the average Joule heating:
\[\bar{P}=U_{ef}\,I_{ef}= R\,{\left(I_{ef}\right)}^2.\]
The average Joule heating calculated here from the maximum value of the current is the same as the average Joule heating calculated above from the effective value of the current:
\[R\,{\left(I_{eff}\right)}^2 \, T=\frac{1}{3}\,RI_{\mathrm{max}}^2T\]And we find the relation between the maximum and the effective current:
\[{\left(I_{eff}\right)}^2 =\frac{1}{3}\,I_{\mathrm{max}}^2\] \[I_{eff} =\frac{I_{\mathrm{max}}}{\sqrt{3}}.\]Comparison of Sawtooth and Harmonic Current
The comparison is summed up in the following table. The values for sawtooth current have been derived above in this task. The values for the harmonic current can be found in the task Heating Power of Alternating Current in Resistor
Sawtooth current: Harmonic current: Average current: \[ I=\frac{I_{\mathrm{max}}}{2} \ \,\] \[ I=0 \ \,\] Effective current: \[ I_{ef}=\frac{I_{\mathrm{max}}}{\sqrt{3}}\ \ \,\] \[ I_{ef}=\frac{I_{\mathrm{max}}}{\sqrt{2}}\ \ \,\] Average power: \[ P=R\,\frac{I_{\mathrm{max}}^2}{3}\ \ \,\] \[ P=R\,\frac{I_{\mathrm{max}}^2}{2}\ \ \,\] Notation and numerical substitution
R = 100 Ω Resistance of the resistor Imax = 2 A Maximum current T = 0.2 s Period of the current \(\bar{I}\) = ? (A) Average current Ief = ? (A) Effective current P = ? (W) Average power
\[\bar{I}=\frac{I_{\mathrm{max}}}{2}=\frac{2}{2}\,\mathrm A=1\,\mathrm A\] \[\bar{P}= R \left(\frac{I_{\mathrm{max}}}{\sqrt{3}}\right)^2=100\cdot \left(\frac{2}{\sqrt{3}}\right)^2\,\mathrm W\overset{\cdot}{=}133\,\mathrm W \] \[I_{eff} =\frac{I_{\mathrm{max}}}{\sqrt{3}}=\frac{2}{\sqrt{3}}\,\mathrm A\overset{\cdot}{=}1.15\,\mathrm A\]Answer
The average value of the given current is 1 A.
The average power is approximately 133 W.
The effective value of the given current is approximately 1.15 A.



