Collection of Solved Problems in Physics

Work done by moving a charge

Task number: 302

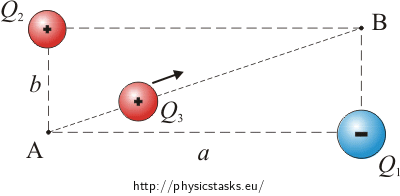
Let’s imagine a rectangle AQ₁BQ₂ with sides a = 15 cm and b = 5 cm.

There are two charges Q₁ = -5 µC and Q₂ = +2 µC placed in vertices Q₁ and Q₂. How much work have to be done by an electric force to move a charge Q₃ = +3 µC diagonaly from the vertex A to the vertex B?

• Hint: Work

  The work done by an electric force is propotional to the amount of the moved charge and proportional to the difference of potentials between the starting point and the destination.

• Hint: Point charge potential

  Point charge potential depends on amount of the charge and on the distance to the charge.

• Analysis

  The work done by an electric force is proportional to the amount of the charge moved and proportional to the difference of the potential in the starting and the potential in the final position. (It’s similar to the work in the field of gravity attraction. Work done by the force is equal to the amount of the potential energy lost.)

  The electric potential in any point is equal to electric potential energy of unitary charge placed in that position. So the electric potential energy is proportional to the electric potential in the same place and to the amount of the charge placed there.

  Our field is generated by two point charges. In this case the net potential field is equal to the sum of both fields.

  The electric field potential of the point charge is proportional to the amount of the charge and inversely proportional to the distance to the charge. The sign is the same as the sign of the charge.

  To solve the task, we have to figure out the potentials in vertices A and B. Then we can enumerate the electric potential energy of the charge Q₃ in these places. The work done by an electric forces by moving the charge from A to B is equal to the difference of these electric potential energies.

• Calculating potential in places A and B

  Work done by an electric force by transfering a charge in an electric field is equal to the difference of potential energies between the starting position A and the final position B.

  \[W\,=\,E_{pA} - E_{pB}\]

  The electric field potential is equal to the potential energy of a charge equal to 1 C. We can determine potential energy using the field potential E_p = Q₃φ and so we can determine the work:

  \[W\,=\,Q_3\left( \varphi_A-\varphi_B\right)\]

  In this part of solution we will determine the potentials in places A and B, the work wil be determined afterwards.

  Electric field potential caused by the first and the second charge in place A is equal to the sum of potentials caused by several charges.

  \[\varphi_A \,=\,\varphi_{1A} + \varphi_{2A}\, ,\tag{(1)}\]

  where φ_1A is the potential caused by the first charge and φ_2A is the potential caused by the second charge in the place A.

  The equation for the potential in the place B is analogous.

  \[\varphi_B\,=\,\varphi_{1B}+\varphi_{2B}\tag{(2)}\]

  The electric field potential of the point charge Q in the distance r from the charge is:

  \[\varphi\,=\,\frac{1}{4 \pi \epsilon_0}\frac{Q}{r}\]

  The distance between the charge Q₁ and the place A is a, so the potential caused by the first charge in the place A is:

  \[\varphi_{1A}\,=\,\frac{1}{4 \pi \epsilon_0}\frac{Q_1}{a}\]

  The distance between the charge Q₁ and the place B is b, so the potential in the place B is:

  \[\varphi_{1B}\,=\,\frac{1}{4 \pi \epsilon_0}\frac{Q_1}{b}\]

  The potential caused by the second point charge is analogous:

  \[\varphi_{2A}\,=\,\frac{1}{4 \pi \epsilon_0}\frac{Q_2}{b}\] \[\varphi_{2B}\,=\,\frac{1}{4 \pi \epsilon_0}\frac{Q_2}{a}\]

  Let’s substitute these formulas into the equation (1) to get total electric potencial in the place A

  \[\varphi_A \,=\,\,\frac{1}{4 \pi \epsilon_0} \left(\frac{Q_1}{a} + \frac{Q_2}{b}\right)\tag{(*)}\]

  and into the equation (2) to get total potential in the place B.

  \[\varphi_B\,=\,\frac{1}{4 \pi \epsilon_0} \left(\frac{Q_1}{b} + \frac{Q_2}{a}\right)\tag{(**)}\]

• Work enumeration

  In previous sections we have mentioned that the work done by the electric force is proportional to the charge and to the difference of potentials in the starting point and the destination.

  \[W\,=\,Q_3\left( \varphi_A-\varphi_B\right)\tag{(*)}\]

  The potentials in places A and B we enumerated in previous section.

  \[\varphi_A \,=\,\,\frac{1}{4 \pi \epsilon_0} \left(\frac{Q_1}{a} + \frac{Q_2}{b}\right)\] \[\varphi_B\,=\,\frac{1}{4 \pi \epsilon_0} \left(\frac{Q_1}{b} + \frac{Q_2}{a}\right)\]

  Now we substitute these potentials into the formula (*) to get the work.

  \[W\,=\,\frac{Q_3}{4 \pi \epsilon_0}\left[ \left(\frac{Q_1}{a} + \frac{Q_2}{b}\right)- \left(\frac{Q_1}{b} + \frac{Q_2}{a}\right)\right]\]

  We have to simplyfy these expression. In the first step let’s group the fractions with the same determinators together.

  \[W\,=\,\frac{Q_3}{4 \pi \epsilon_0}\left( \frac{Q_1}{a} + \frac{Q_2}{b}- \frac{Q_1}{b} - \frac{Q_2}{a}\right)\,=\,\frac{Q_3}{4 \pi \epsilon_0}\left( \frac{Q_1-Q_2}{a} + \frac{Q_2-Q_1}{b} \right)\]

  Now we can modify the numerator of the second part to the same form as the first one.

  \[W\,=\,\frac{Q_3}{4 \pi \epsilon_0}\left( \frac{Q_1-Q_2}{a} - \frac{Q_1-Q_2}{b} \right)\]

  And finally we exclude the numerators.

  \[W\,=\,\frac{Q_3\left(Q_1-Q_2\right)}{4 \pi \epsilon_0}\left( \frac{1}{a} - \frac{1}{b} \right)\]

• Numerical substitution

  \[a\,=\,15\,\mathrm{cm}\,=\,1{,}5{\cdot}10^{-1}\,\mathrm{m}\] \[b\,=\,5\,\mathrm{cm}\,=\,5{\cdot}10^{-2}\,\mathrm{m}\] \[Q_1\,=\,-5\,\mathrm{\mu C}\,=\,-5{\cdot}10^{-6}\,\mathrm{ C}\] \[Q_2\,=\,+2\,\mathrm{\mu C}\,=\,+2{\cdot}10^{-6}\,\mathrm{ C}\] \[Q_3\,=\,+3\,\mathrm{\mu C}\,=\,+3{\cdot}10^{-6}\,\mathrm{ C}\] \[W\,=\,?\,\left(\mathrm{J}\right)\]

  From tables:

  \[\varepsilon_0\,=\,8{,}85{\cdot} 10^{-12}\,\mathrm{ C^2\,N^{-1}\,m^{-2}}\]

  ---

  \[W\,=\,\frac{Q_3\left(Q_1-Q_2\right)}{4 \pi \epsilon_0} \,\left(\frac{1}{a} - \frac{1}{b} \right)\] \[W\,=\,\frac{3{\cdot}10^{-6}\left(-5{\cdot}10^{-6}-2{\cdot}10^{-6}\right)}{4 \pi\cdot 8{,}85{\cdot} 10^{-12}} \,\cdot\left(\frac{1}{1{,}5{\cdot}10^{-3}} - \frac{1}{5{\cdot}10^{-2}} \right)\,\mathrm{J}\] \[W\,=\,2{,}5 \, \mathrm{J}\]

• Answer

  By moving the charge from the vertex A to the vertex B the elektrical force have done the work

  \[W\,=\,\frac{Q_3\left(Q_1-Q_2\right)}{4 \pi \epsilon_0} \,\left(\frac{1}{a} - \frac{1}{b} \right)\,=\,2{,}5\,\mathrm{J}.\]

• What if the work is negative?

  The negative work is in the situation where the charge was moved from the place with lower potential energy to the palce with higher potential energy. In this case the work was not done by the electric force but by some external force.

  It is the same as in the gravitational potential field. If an object falls (is moving from the place with higher potential energy to the place with lower potential energy), the work is done by the gravitational force. On the other hand if we want to move the object from a place with lower potential energy to a place with higher potential energy, the work has to be tone by some external force.

  The work done by the electric force and by some external force are of the same size but differs in the sign (such is the convention).