Collection of Solved Problems in Physics

Magnetic Field of a Straight Conductor inside a Solenoid

Task number: 1780

• Hint

  Draw the magnetic fields produced by the straight conductor and by the solenoid.

  What must the two contributions be to sum up to a vector declined by 45° from the axis?

• Figure

  Cross-section of the field inside the solenoid:

  The magnetic field lines of the solenoid are green, the field lines of the straight conductor are blue.

  

   

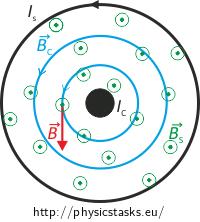
  Radial section along the solenoid

  The magnetic field lines of the solenoid are green, the field lines of the straight conductor are blue.

  

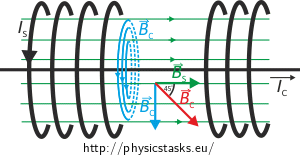
  Note: A very long solenoid is considered, the figure shows only its part. The turns are present along the whole length of the solenoid; they are not drawn in the middle part of the picture so that we can “see inside”.

• Analysis

  Because both the solenoid and the straight conductor carry currents, magnetic fields are produced in their surroundings.

  The magnetic field of the solenoid is parallel to its axis (inside the solenoid). It is also parallel to the conductor that runs through it (see the Figure). The magnetic field of the straight conductor forms concentric circles with the conductor in their center. It follows that the B‑field of the solenoid and that of the straight conductor are perpendicular to each other at each point inside the solenoid in our case.

  Two perpendicular vectors must have the same magnitude to sum up to a total B‑field vector that forms an angle of 45° with each of them (and with the axis). The magnitude of the B‑field of the solenoid does not change with the position anywhere inside the solenoid (it is constant there). The B‑field of the straight conductor decreases with the distance from the conductor. We thus have to find the distance from the straight conductor at which the magnitude of the B‑field of the straight conductor is equal to the magnitude of the B‑field of the solenoid.

  

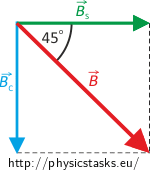
• Solution

  The magnitude of the magnetic field B_C of a straight conductor is given by

  \[ B_C=\frac{\mu_0 I_C}{2\pi R}, \]

  where I_C is the current flowing through the conductor and r is the distance between the conductor and the point of interest.

  The magnitude of the magnetic field B_S of a solenoid is given by

  \[B_S=\mu_0 I_S n\]

  where I_S is the current flowing through the solenoid, n is the number of turns per unit length and μ₀ is the permeability of vacuum.

  It was explained in the analysis and it can be seen in the figures that the total magnetic B‑field forms an angle of 45° with the solenoid axis, when:

  \[ B_C=B_S \]

  Let us substitute the formulas for B_C and B_S above to the latter one:

  \[ \frac{\mu_0I_C}{2\pi R}=\mu_0I_Sn \]

  and express the unkown radial distance R:

  \[ R=\frac{I_C}{2\pi I_Sn}. \]

  The magnitude of the total magnetic induction in the distance R from the axis of the solenoid and from the conductor is calculated as follows (see the Figure):

  \[ B = \frac{B_S}{\cos 45^{\circ}} \]

• Notation and numerical substitution

  \(n=10\,\mathrm{cm^{-1}}=1000\,\mathrm{m^{-1}}\)	length density of the turns of the solenoid
  \(r=7\,\mathrm{cm}=0{,}070\,\mathrm{m}\)	solenoid radius
  \(I_S =20\,\mathrm{mA}=0{,}020\,\mathrm{A}\)	current through the solenoid
  \(I_C =6\,\mathrm{A}\)	current through the straight conductor
  \(R=?\,\mathrm{(cm)}\)	distance from the axis of the solenoid at which the axis and the vector of the B‑field form an angle of 45°
  \(B=?\,\mathrm{(B)}\)	magnitude of the magnetic B‑field

  ---

  \[R=\frac{I_C}{2\pi I_Sn}=\frac{6}{2\pi\cdot0{,}02{\cdot}1000}\,\mathrm{m}=0{,}048\,\mathrm{m}=4{,}8\,\mathrm{cm}\] \[B=\frac{B_S}{\cos45^{\circ}}=\frac{\mu_oI_Sn}{\cos45^{\circ}}=\dfrac{4\pi\cdot10^{-7}\cdot0{,}02{\cdot}1000}{\dfrac{\sqrt{2}}{2}}\,\mathrm{T}\dot{=} 3{,}554{\cdot}10^{-5}\,\mathrm{T} \,\dot{=}\, 36\,\mathrm{\mu T}\]

• Answer

  The vector of the total magnetic B‑field makes an angle of 45° with the solenoid axis in a distance of 4.8 cm from the solenoid axis. The magnitude of the B‑field is approximately B = 36 μT at this point.