Heating Power of Alternating Current in Resistor
Task number: 1782
Deduce, what direct current must flow through a resistor to produce the same heating power as an alternating current with a peak value of 3.5 A?
Hint 1
Look up the formula of electrical power delivered to an element in a direct current (DC) circuit. In an alternating current (AC) circuit, both the current and the voltage change in time and thus the power does also change in time. This means that we are going to compare the mean value of the power in the AC circuit to the power in the DC circuit.
Hint 2
The mean value of the power in the alternating current circuit should be equal to the power in the direct current circuit.
Analysis
We are going to solve this task using the work of the electric current. We could also directly compare the average value of the power delivered by the alternating current with the power delivered by the direct current in the same circuit.
We calculate the work done by the direct current as the product of the heating power delivered by the current in the resistor and of the time during which the current does the work.
We know the peak value of the alternating current from the assignment. For this reason, we rearrange the formula of the delivered power so that it features this current and the value of the resistance of the resistor. The resistance of the resistor is the same for both circuits. We determine the mean value of the power and the work delivered over the given time with the help of the plot of the instantaneous power of the alternating current.
We obtain the relation between the direct current and the alternating current by comparing the work delivered by these currents in the same circuit.
Solution - Derivation of Relation between Effective and Peak Value of Alternating Current
We describe the power delivered by a resistor in the DC circuit with the formula:
\[P=VI\mathrm{.}\]We rewrite this relation using Ohm’s law:
\[V=IR\]into the form that features the resistance of the resistor and current:
\[P=RI^2\mathrm{.}\]The current and the voltage change with time in AC circuits and so does the power, subsequently, because the power is the product of the former two quantities.
The instantanenous value of power in the AC circuit is expressed by the formula:
\[p(t)=v(t)\, i(t).\]If there is only a resistor connected in the AC circuit, the phase shift between the current and the voltage is zero and it follows that:
\[v(t)=R\, i(t).\]We can again rewrite the formula of the instantaneous power using Ohm’s law into the following from:
\[p(t)=R \, \left[ i(t) \right]^2\]The total work over time t is equal to the area under the graph of the function p(t). First, we show this on the graph of the power of the direct current.
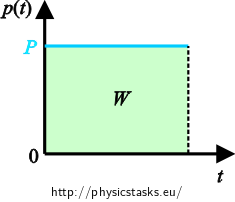
The power in the DC circuit is constant and the delivered work thus is:
\[W=P\cdot t\]We can see that work indeed corresponds to the area under the graph.
The course of the instantaneous power in the AC circuit is depicted in the following figure:
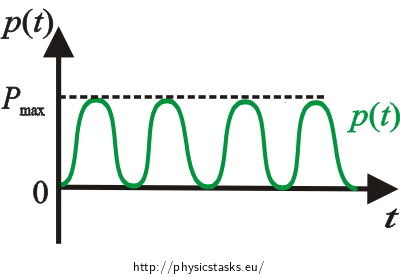
Work is calculated as the area under the graph of the instantaneous power p(t).
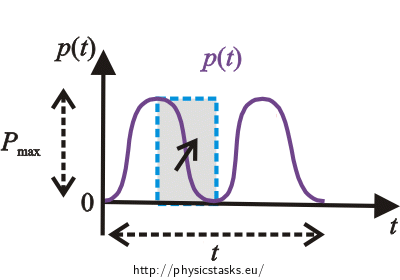
Looking at the power graph, we see that the curve splits the indicated rectangle into two equal parts. For this reason, we calculate the average value of work as:
\[W=\frac{P_{\mathrm{max}}\,t}{2}\]It holds that the maximum power is given by the maximum current:
\[P_{\mathrm{max}}=R\left(I_{\mathrm{max}}\right)^2,\]and we obtain the work of the alternating current as:
\[W=\frac{1}{2}R\left(I_{\mathrm{max}}\right)^2t\]The direct current would, over the same time, deliver the work:
\[W=RI^2t.\]We set equal the work delivered in the DC circuit to the work delivered in the AC circuit. In this way we obtain the ratio between the currents that are needed to deliver the same work in these two types of circuit:
\[\frac{1}{2}R\left(I_{\mathrm{max}}\right)^2t=R I^2 t\] \[\frac{1}{2}\left(I_{\mathrm{max}}\right)^2=I^2\] \[I=\frac{I_{\mathrm{max}}}{\sqrt2}.\]Solution Comment
One can imagine the total work as the sum of narrow rectangles stretched vertically between the t axis and the curve of the instantaneous power - each of them has a width of a small time interval Δt and the height of the instantaneous power p(t) in that time interval. The area of the narrow rectangle at time t is p(t)·Δt and the total area under the curve of power, representing the total work, is approximately equal to the sum of the areas of these narrow rectangles:
\[W\approx\sum{p(t)\Delta t}\]Summation with infinitely narrow time intervals dt is called integration and gives the exact value of the area under the curve p(t):
\[W=\int_t{p(t)}\,\mathrm{d}t.\]Numerical Solution
The value of the alternating current:
\[I=\frac{I_{\mathrm{max}}}{\sqrt2}=\frac{3{,}5}{\sqrt2}\,\mathrm A\,\dot{=}\,2.5\,\mathrm A\]
Answer
The direct current flowing through a given resistor has to be about 2.5 A to produce the same heating power as the alternating current with a peak value of 3.5 A.
Comment - Definition of Effective Value of Alternating Current
We have in fact derived the relation between the maximum and the effective value of the alternating current because the effective value of the alternating current is indeed defined as the value of the direct current that delivers the same work in the same circuit as the given alternating current over the same time (many periods).
We can also say that the effective value of the alternating current is defined by the value of the direct current whose power in a circuit is equal to the mean value of the power of the alternating current in the same circuit.




