Unevenly Charged Ball
Task number: 1532
A ball with radius R is unevenly charged with a charge of bulk density proportional to a distance form the centre of the ball: ρ = Kr, where K is a constant.
a) Find the equation describing the electric field intensity at a distance z from the centre of the ball.
b) Determine the electric potential of the ball at a distance z.
Consider a field inside and outside the ball, i.e. find the behaviour of electric intensity and electric potential as a function of distance z from the centre of the ball in the interval "from zero to infinity".
Hint: Intensity
Given the fact that for solving this task we apply Gauss's law, we need to decide how we choose the Gaussian surface.
We choose a surface of a sphere of radius z centred in the midpoint of the ball to be the Gaussian surface. In such a case the vector of electric field intensity is at all points perpendicular to the surface and of the same magnitude.
We divide this task into two parts:
- The radius of the Gaussian sphere is larger than the radius of the charged ball.
- The radius of the Gaussian sphere is smaller than the radius of the charged ball.
Hint: Calculating the charge contained in the ball
Because the density of the charge distribution is not constant, we need to calculate the size of the charge contained in the ball using an integral.
We can imagine that the ball is composed of numerous thin shells. The total charge can be obtained by adding the charge on all shells together.
\[Q\,=\,\int \mathrm{d}Q\,=\, \int_V \varrho \, \mathrm{d}V\,,\] where dV is the volume of one shell.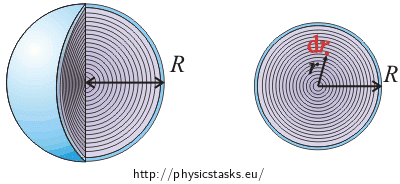
Now we have to evaluate the volume dV of individual shells. The shells are very thin; we can therefore determine their volume by multiplying the surface of the shell by its thickness. Each shell of radius r and thickness dr has a volume dV:
\[\mathrm{d}V\,=\, 4 \pi r^2 \mathrm{d}r\,.\]We integrate across the whole ball, i.e. over r from 0 to the radius of the ball R.
\[Q\,=\, \int_0^R 4 \pi \varrho r^2\,\mathrm{d}r\]Hint: Electric potential
Potential is potential energy per unit charge
\[\varphi\,=\, \frac{E_p}{Q}\]and potential energy Ep at a given point is equal to negative taken work of electric force required to transfer a charge from a point of zero potential energy (in our case from infinity) to this point.
\[E_p(z)\,=\, - \int^z_{\infty} \vec{F} \cdot \mathrm{d}\vec{z}\]Now we substitute the integral.
\[\varphi\,=\, - \int^z_{\infty} \frac{\vec{F}} {Q}\cdot \mathrm{d}\vec{z}\]Force F divided by charge Q is electric field intensity \(\vec{E}\).
\[\varphi\,=\, - \int^z_{\infty} \vec{E}\cdot \mathrm{d}\vec{z}\]Analysis: Intensity
We divide this task into two parts. We examine the field inside the charged ball and the field outside the ball separately.
Due to a symmetrical charge distribution, the easiest way to find the electric field intensity is to use Gauss's law of electrostatics. Gauss's law relates an electric flux through a closed area and a total charge enclosed in this area.
The vector of electric intensity points from the centre of the ball at all points, and its magnitude depends only on the distance from the centre of the ball. This is due to the symmetrically distributed charge inside the ball. The following idea can help: Charge is distributed symmetrically inside the ball, therefore we can not see any difference if we rotate the ball around any axis passing through the centre of the sphere. The field around the ball must remain the same; therefore the intensity vector must have the same direction and magnitude at any rotation.
The Gaussian surface is chosen to be a sphere centred in the midpoint of the charged ball. In this case, the vector of electric intensity is of the same magnitude and perpendicular to the surface at all points of the surface. Thus we simplify the calculation of the flow of electric field intensity in Gauss's law.
When determining the intensity outside the ball, the Gaussian sphere radius is greater than the radius of the charged ball. Inside the Gaussian surface is closed the whole charge.
When determining the intensity inside the charged ball, the radius of the Gaussian sphere is smaller than the one of the charged ball. We evaluate the charge enclosed in the Gaussian sphere by using the charge bulk density.
The charge is not distributed in the ball with constant density. To calculate the total charge in the ball or the charge enclosed within the Gaussian sphere, we use the integral.
Solution: Intensity outside the ball
In this section we determine the intensity of the electric field outside the charged ball, i.e. for z > R.
We use Gauss’s law:
\[\oint_S \vec{E} \cdot \mathrm{d}\vec{S}\,=\, \frac{Q}{\varepsilon_0}\,,\] \[\oint_S \vec{E} \cdot \vec{n}\mathrm{d}S\,=\, \frac{Q}{\varepsilon_0}\,.\tag{*}\]The charge is distributed in the ball symmetrically; therefore the electric field in the vicinity of the ball is also symmetrical. The vector of electric intensity points at all points of the ball from the ball midpoint (i.e. it is perpendicular to the surface of the ball), and its magnitude depends only on the distance from the centre of the ball.
We choose the Gaussian surface to be a surface of a sphere with radius z and its centre in the midpoint of the ball (in the figure indicated by green). We choose this surface, because the vector of electric intensity is perpendicular to this surface and is of a constant size, which simplifies the calculation.
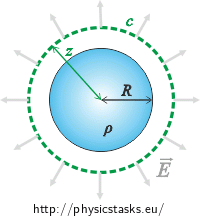
Note: The brightness of the colour represents the charge density
The vector of electric field intensity E (gray) is at all points parallel to a normal vector of the surface and we can easily determine their scalar product:
\[\vec{E} \cdot \vec{n}\,=\,En\,=\,E\,.\](Note: The last equality is true because \(\vec{n}\) is a unit vector).
Using this knowledge we can adjust the integral on the left side of Gauss's law:
\[\oint_c \vec{E} \cdot \vec{n}\mathrm{d}S\,=\,\oint_c E n\mathrm{d}S\,=\, \oint_c E\mathrm{d}S\]The vector of electric field intensity E is at all points of the surface of the same magnitude (is constant); therefore it can be factored out of the integral as a constant. We obtain a relationship
\[\oint_c \vec{E} \cdot \vec{n}\mathrm{d}S\,=\,E \oint_c \mathrm{d}S\]Now we determine the integral.
\[\oint_c \vec{E} \cdot \vec{n}\mathrm{d}S\,=\,E S_s\]where Ss = 4πz2 is the surface of the Gaussian sphere.
\[\oint_c \vec{E} \cdot \vec{n}\mathrm{d}S\,=\,E\, 4 \pi z^2\]The resulting relationship is substituted back into Gauss's law (*).
\[E 4 \pi z^2\,=\, \frac{Q}{\varepsilon_0}\]We evaluate the magnitude of electric intensity.
\[E \,=\, \frac{1}{4 \pi \varepsilon_0}\,\frac{Q}{z^2}\tag{**}\]The formula is the same as the one for the electric field in the vicinity of a point charge. A symmetrically charged ball forms in its surroundings the same field as the field around a point charge.
Now we only need to evaluate the charge Q in the selected Gaussian surface using the given values.
The whole charged ball is contained inside the surface. Because the charge is distributed with constant density, we use an integral to calculate the total charge of the ball.
We can imagine that the ball is composed of numerous thin shells. The total charge can be obtained by adding the charge on all shells together.
\[Q\,=\,\int \mathrm{d}Q\,=\, \int_V \varrho \, \mathrm{d}V\,,\] where dV is a volume of a shell.
Now we have to evaluate the volume dV of an individual shell. Given the fact that the shells are very thin, we can express their volume as a product of the shell surface and its thickness. Each shell of radius r and thickness dr has a volume dV:
\[\mathrm{d}V\,=\, 4 \pi r^2 \mathrm{d}r\,.\]We integrate across the whole ball, i.e. over r from 0 to the radius of the ball R.
\[Q\,=\, \int_0^R \varrho 4 \pi r^2\,\mathrm{d}r\,=\, \int_0^R 4 \pi K r^3\,\mathrm{d}r\]We factor the constants out of the integral and we calculate the integral.
\[Q\,=\, 4 K \pi \int_0^R r^3\,\mathrm{d}r \,=\,4 K \pi \left[ \frac{r^4}{4} \right]_0^R\,=\,4 K \pi \,\frac{R^4}{4}\] \[Q\,=\, K \pi R^4\]We substitute the calculated charge into the formula (**) and we adjust the formula.
\[E \,=\, \frac{1}{4 \pi \varepsilon_0}\,\frac{K \pi R^4}{z^2}\,=\, \frac{K R^4}{4 \varepsilon_0\,z^2}\]At a distance z the electric field intensity of the charged ball is:
\[E \,=\, \frac{K R^4}{4 \varepsilon_0} \, \frac{1}{z^2} \,.\]Solution: Intensity inside the ball
In this section we evaluate the intensity of electric field inside the charged ball. The procedure is very similar to the one in the previous section Intensity outside the ball, so this section is not described in detail.
We determine the electric intensity by Gauss's law:
\[\oint_c \vec{E} \cdot \mathrm{d}\vec{S}\,=\, \frac{Q_1}{\varepsilon_0}\,,\tag{*}\]where Q1 is the charge inside the Gaussian surface.
We choose the Gaussian surface to be a surface of a sphere centred in the midpoint of the charged ball with the radius z < R.
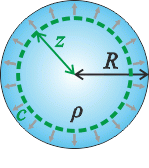
The integral on the left side is calculated as in the previous section.
\[\oint_c \vec{E} \cdot \vec{n} \mathrm{d}S\,=\, \frac{Q_1}{\varepsilon_0}\]Using the same reasoning about symmetry as in the previous section, we derive the vector of electric intensity to be on the whole surface of the same magnitude and perpendicular to the Gaussian surface, therefore the following applies:
\[\oint_c \vec{E} \cdot \mathrm{d}\vec{S}\,=\,\oint_c En \mathrm{d}S\,=\,\oint_c E \mathrm{d}S\,=\,E\oint_c \mathrm{d}S.\]The integral is equal to the surface of the Gaussian sphere.
\[\oint_c \vec{E} \cdot \mathrm{d}\vec{S}\,=\,E S_s\,=\,E\, 4 \pi z^2\,\]The resulting relationship is substituted back into Gauss's law (*)
\[E\, 4 \pi z^2\,=\, \frac{Q_1}{\varepsilon_0}\tag{***}\]Now we evaluate the charge Q1. Given the fact that the Gaussian sphere is smaller than the charged ball, only a part of the ball charge is closed within the sphere. To calculate the charge we again use the integral because the charge density is not constant.
We can imagine that the ball is composed of thin shells. The total charge is obtained by summing the charge of individual shells. (See detailed commentary in the previous section.)
\[Q_1\,=\, \int\mathrm{d}Q\,\,=\, \int_V \varrho \,\mathrm{d}V\]We express the volume of an individual shell. Because we integrate over the radius of the Gaussian sphere, the integration limits are from 0 to z.
\[Q_1\,=\, \int_0^z \varrho 4\pi r^2 \,\mathrm{d}r\,=\, \int_0^z 4\pi K r^3 \,\mathrm{d}r\]We factor the constants out of the integral and calculate the integral.
\[Q_1\,=\, 4 K \pi \int_0^z r^3\,\mathrm{d}r \,=\,4K \pi \left[ \frac{r^4}{4} \right]_0^z\,=\,4 K \pi \,\frac{z^4}{4}\] \[Q_1\,=\,K \pi z^4\]By substituting into Gauss's law (***) we obtain
\[E \,4\pi z^2\,=\, \frac{K \pi z^4}{\varepsilon_0}\]And we evaluate the magnitude of the electric field inside the charged ball.
\[E \,=\, \frac{K}{4 \varepsilon_0}\,z^2\]Analysis: Potential
Electric potential can be determined by electric intensity. The potential at a given point is equal to negative taken integral of electric intensity from the point of zero potential to the given point. Zero potential is selected in infinity. (A more detailed explanation is given in Hint.)
When calculating the potential inside the charged ball we must take into account that the electric field intensity is not described by the same expression along the path of integration; it is described by different equations inside and outside the ball. Therefore, we must first calculate the work that is needed to transfer a unit charge to the surface of the charged ball, and then the work required to transfer the charge inside the ball.
Solution: Potential outside the ball
The potential at point A is equal to a negative taken integral of intensity from a point of zero potential to the point A. Zero potential is selected in infinity. (A more detailed explanation is given in Hint.)
\[\varphi (z)\,=\, - \int_{\infty}^z \vec{E} \cdot \mathrm{d}\vec{z}\]The electric field intensity is dependent only on the distance from the centre of the ball; therefore the potential also depends on the distance from the centre of the ball.
The potential does not depend on the choice of the integration path so it can be freely selected. (We choose the simplest path.) In this case, we choose the path of integration to be a part of a straight line which extends into the centre of the ball.
The electric field intensity vector \(\vec{E}\) is parallel to the \(\vec{z}\) vector. Therefore, we can simplify the integral.
\[ \varphi (z)\,=\, - \int^{z}_{\infty} E \mathrm{d}z \]Now we have to divide the task into two cases and calculate the potential inside and outside the ball separately.
First, we evaluate the potential at a distance z outside the ball.
\[\varphi (z)\,=\, - \int^{z}_{\infty} E \mathrm{d}z \]We substitute the magnitude of electric intensity evaluated in the section The field intensity outside the ball into the integral.
\[E \,=\, \frac{K R^4}{4 \varepsilon_0} \, \frac{1}{z^2} \]and factor all constants out of the integral:
\[\varphi (z)\,=\, - \int^{z}_{\infty} \frac{K R^4}{4 \varepsilon_0}\,\frac{1}{z^2} \,\mathrm{d}z \,=\, - \, \frac{K R^4}{4 \varepsilon_0} \int^{z}_{\infty} \frac{1}{z^2}\, \mathrm{d}z\]Now we determine the definite integral
\[\varphi (z)\,=\,- \, \frac{K R^4}{4 \varepsilon_0}\,\left[- \frac{1}{z}\right]^z_{\infty}\,.\]We substitute the limits of the integral and we obtain the size of the potential outside the ball at the distance z:
\[\varphi (z)\,=\, \frac{K R^4}{4 \varepsilon_0}\,\frac{1}{z}\]Note: If we substitute for the constant K the formula describing the total charge \(Q\,=\, K \pi R^4 \), we obtain the same relationship as for the potential for a point charge, i.e.
\[\varphi (z)\,=\, \frac{Q}{4 \pi \varepsilon_0}\,\frac{1}{z}\,.\]Solution: Potential inside the charged ball
When calculating the potential inside the ball we proceed as in the previous section. The potential is expressed by the equation: \[ \varphi (z)\,=\, - \int^{z}_{\infty} \vec{E} \cdot \mathrm{d}\vec{z}\,=\, - \int^{z}_{\infty} E \mathrm{d}z\,. \]When expressing the potential we have to take into account the magnitude of electric intensity. This time the electric intensity is not described by the same equation along the path of integration. The point where the intensity equation changes, is the surface of the ball. Therefore, we have to divide the integral into two separate integrals. First, we have to transfer the charge from infinity to the surface of the ball (i.e. to the distance R from the centre of the ball) and then from the surface of the ball further inside the ball.
\[\varphi (z)\,=\, - \int^{R}_{\infty} E_out \mathrm{d}z - \int^{z}_{R} E_in \mathrm{d}z \]We substitute the magnitude of electric intensity that we have evaluated in previous sections
\[E_out \,=\, \frac{K R^4}{4 \varepsilon_0} \, \frac{1}{z^2}\] \[E_in \,=\, \frac{K}{4 \varepsilon_0}\,z^2\]and we obtain
\[\varphi (z)\,=\, - \int^{R}_{\infty} \frac{K R^4}{4 \varepsilon_0} \, \frac{1}{z^2}\, \mathrm{d}z - \int^{z}_{R} \frac{K}{4 \varepsilon_0}\,z^2 \, \mathrm{d}z\,.\]We factor all constant out of the integrals
\[\varphi (z)\,=\, - \frac{K R^4}{4 \varepsilon_0}\int^{R}_{\infty} \frac{1}{z^2}\, \mathrm{d}z\, - \frac{K}{4 \varepsilon_0}\int^{z}_{R} z^2 \,\mathrm{d}z \]and we calculate the integrals.
\[\varphi (z)\,=\,- \frac{K R^4}{4 \varepsilon_0} \left[- \frac{1}{z}\right]^R_{\infty}- \frac{K}{4 \varepsilon_0}\left[\frac{z^3}{3}\right]^z_{R}\] \[\varphi (z)\,=\,- \frac{K R^4}{4 \varepsilon_0}\left(- \frac{1}{R}\right)- \frac{K}{4 \varepsilon_0}\left(\frac{z^3}{3}-\frac{R^3}{3}\right)\]Note: It is not necessary to calculate the first integral. We can substitute z = R into the result of the previous section.
We factor \(\frac{K}{4 \varepsilon_0}\) out and adjust the formula.
\[\varphi (z)\,=\, \,\frac{K}{4 \varepsilon_0}\left(R^3 - \,\frac{z^3}{3} + \frac{R^3}{3}\right)\] \[\varphi (z)\,=\, \,\frac{K}{4 \varepsilon_0}\left(\frac{4R^3}{3} - \,\frac{z^3}{3} \right)\] \[\varphi (z)\,=\, \,\frac{K R^3}{12 \varepsilon_0}\left(4 - \frac{z^3}{R^3} \right)\]We have obtained an equation for potential inside the charged ball.
Answer
The electric intensity outside the ball is described by the formula
\[E \,=\, \frac{KR^4}{4 \varepsilon_0} \, \frac{1}{z^2}\,=\, \frac{1}{4 \pi \varepsilon_0}\,\frac{Q}{z^2}\,. \]Inside the ball it is described by
\[E \,=\, \frac{K}{4 \varepsilon_0}\,z^2\,.\]In both cases, the electric field intensity vector points towards or outwards the centre of the charged ball, depending on the sign of the charge.
The electric potential outside the ball is described by
\[\varphi (z)\,=\, \frac{KR^4}{4 \varepsilon_0}\,\frac{1}{z} \,=\, \frac{Q}{4 \pi \varepsilon_0}\,\frac{1}{z} \,.\]The electric potential inside the ball is described by
\[\varphi (z)\,=\, \,\frac{KR^3}{12 \varepsilon_0}\left(4 - \frac{z^3}{R^3} \right)\,.\]Graphs
Graph of electric intensity as a function of a distance z from a centre of a ball
Inside a charged ball the electric intensity is \(E \,=\, \frac{K}{4 \varepsilon_0}\, z^2 \,.\)
Outside the ball the it is described by the relation \(E\,=\, \frac{ KR^4}{4 \varepsilon_0\,}\,\frac{1}{z^2}\,.\)
The first part of the graph (for z values from 0 to R) forms part of a parabola that passes through the origin. For distance z greater than R the intensity decreases with the square of z.
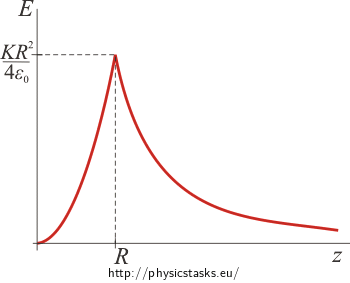
The function is continuous. We prove it by substituting z = R into both relations for electric intensity. In both cases the size of the electric field intensity is \(E(R)\,=\,\frac{KR^2}{4 \varepsilon_0}\,.\)
Note: The electric field intensity is continuous with the exception of points on a charged surface. When passing through a charged surface, only the tangent components of the vector remain continuous. The normal components change "by steps", which are proportional to the area density of the charge. In this task, however, there are no charged surfaces.
Graph of electric potential as a function of a distance from a centre of a ball
The electric potential inside a charged ball has a size of \(\varphi (z)\,=\, \,\frac{KR^3}{12 \varepsilon_0}\left(4 - \frac{z^3}{R^3}\right)\,.\)
Outside the ball it is described by the relation \(\varphi (z)\,=\, \,\frac{KR^4}{4 \varepsilon_0}\frac{1}{z}\,.\)
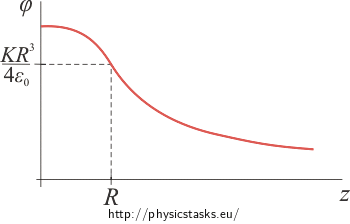
The function is again at the point z = R continuous. If we substitute in both expression describing the potential, we obtain in both cases the value \(\varphi(R) \,=\,\frac{KR^3}{4 \varepsilon_0}\).
Moreover, the function has continuous first derivative at this point; it is therefore smooth.
The electric potential is always continuous, because it is actually the work done by transferring a unit charge and it can not be changed "by steps". With the exception of points on charged surfaces, the first derivative of the potential is also continuous, i.e. the potential is a smooth function.
Link to similar task
The task Pole rovnoměrně nabité koule (in Czech only) is more simple, because the charge is distributed in the charged ball with constant density. .



