Application of Kirchhoff’s laws for calculation of total resistance in a circuit
Task number: 2342
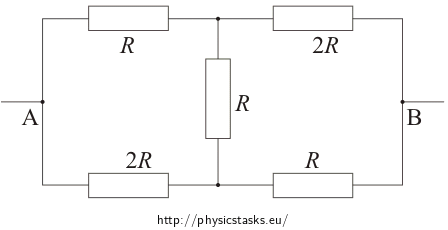
In the picture we can see the schematic of a circuit with 5 resistors. Determine the total resistance between points A and B. Values of resistance for each resistor are shown in the picture.
Hint
Look up Kirchhoff’s laws and try to use them.
Breakdown
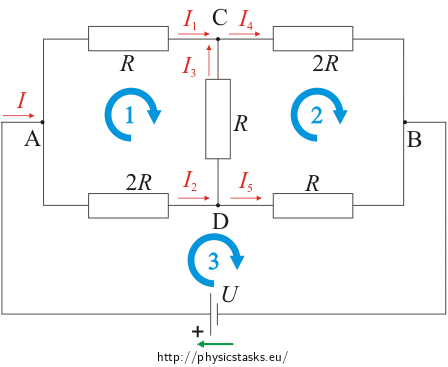
1. Let’s say we have connected the circuit in points A, B to the voltage supply U (we assume that the voltage supply has internal resistance equal to zero).
2. At the voltage supply we shall draw an arrow in the direction of electromotive voltage.
3. In the picture we indicate the currents and choose their direction.
4. We can choose closed loops and their direction.
5. Assemble the equations following the first and second Kirchhoff’s laws.
6. Now we solve the equations.
The more detailed usage of Kirchoff’s laws can be found in assignment Using Kirchhoff’s laws to solve circiut with two power supplies.
First part of solution – assembling of the equations
Resistance between points A and B we can calculated with Ohm´s law:
\[U\,=\, R_\mathrm{total}I\,.\]So, we have to calculate total current in the circuit if we connect it to the voltage supply U.
From the first Kirchhoff’s law we get equations for 4 knots:
\[I\,=\, I_1 + I_2\,=\, I_4 + I_5\tag{knots A, B}\] \[I_1 + I_3\,=\, I_4\tag{knot C}\] \[I_2\,=\, I_3 + I_5\tag{knot D}\]From the second Kirchhoff’s law we get the following equations:
\[RI_1 - RI_3 - 2RI_2\,=\, 0\,\Rightarrow\,I_1-I_3-2I_2\,=\,0\tag{loop 1}\] \[RI_3 + 2RI_4 - RI_5\,=\, 0\,\Rightarrow\,I_3+2I_4-I_5\,=\,0\tag{loop 2}\] \[U\,=\, 2RI_2 + RI_5\tag{loop 3}\]Now we have 6 equations for 6 unknown currents (I, I1, I2, I3, I4, I5).
With this we have completed the solution from the physics point of view. In order to get the final solution we need to solve the simultaneous equations.
Second part of the solution – solution for system of linear equations
After we have summed up equations for loop 1 and loop 2 we get equation:
\[I_1 - 2I_2 - I_5 + 2I_4\,=\,0\,.\]In this equation we can substitute currents I1 and I5 from equation (knots A, B):
\[I_1\,=\, I - I_2\,,\hspace{20px}I_5\,=\, I - I_4\,,\]
then we get the following equation
\[I - I_2 - 2I_2\,=\, I - I_4 - 2I_4\]therefore we get the following relations
\[I_2\,=\, I_4\hspace{20px}\mathrm{a}\hspace {20px}I_1\,=\, I_5\,.\]
After using these relations, our system of linear equations gets simplified:
\[I\,=\,I_1+I_2\tag{1}\] \[I_1+I_3\,=\,I_2\tag{2}\] \[I_1-I_3-RI_2\,=\,0\tag{3}\] \[U\,=\,2RI_2+RI_1\tag{4}\]Into the third equation (3) we can substitute I3 from the second equation (2):
\[ I_1 - (I_2-I_1) - 2I_2\,=\, 0 \] \[ 2I_1 - 3I_2\,=\, 0\,.\]and finally we have relation for I1:
\[I_1\,=\, \frac{3}{2}I_2\,.\]To calculate total resistance we don´t need the rest of the unknowns, therefore we don´t need to calculate the system of linear equations after this point.
Third part of the solution – calculation of total resistance
Now from Ohm´s law we have
\[U\,=\, R_\mathrm{total}I\, =\, R_\mathrm{total}(I_1 + I_2)\]we can substitute Rtotal from previous equation:
\[R_\mathrm{total}\,=\, \frac{U}{I_1+I_2}\,.\]From the second Kirchhoff’s law we already know (equation (4) in last paragraph) that
\[U\,=\,2RI_2+RI_1\,,\]and in the previous paragraph we calculated
\[I_1\,=\,\frac{3}{2}I_2\,.\]After we substitute from these equations to the equations for total resistance we get our total resistance
\[R_\mathrm{total}\,=\, \frac{2RI_2+RI_1}{I_1+I_2}\,=\,\frac{2RI_2+\frac{3}{2}RI_2}{\frac{3}{2}I_2+I_2}\] \[R_\mathrm{total}\,=\, \frac{R(2+\frac{3}{2})I_2}{(\frac{3}{2}+1)I_2}\,=\, \frac{7}{5}R\,.\]Simplification
Because the circuit is “symmetrical“, there is a known physical reason for currents I1 and I5 to be different. This principle also holds for currents I2 and I4.
From Kirchhoff’s laws we immediately get following equations:
\[I\, =\, I_1 + I_2\tag{1.KL, knot A}\] \[I_1+I_3 \,=\, I_2\tag{2.KL, knot C}\] \[RI_1 - RI_3 - 2RI_2 \,=\, 0\tag{loop 2}\] \[U\,=\,2RI_2+RI_1\tag{loop 3}\]And we are already in the second half of the second part of the solution.
Answer
Total resistance of the system of resistors given by the first picture between point A and B is \(R_\mathrm{total}\,=\, \frac{7}{5}R\).
Similar assignment
Using Kirchhoff’s laws to solve circiut with two power supplies is simpler version of this assignment.
Other resolution methods
This assignment can be also solved by transformation of the “triangle“ to a “star“ (to see Transformace trojúhelník - hvězda; in Czech only).







