Collection of Solved Problems in Physics

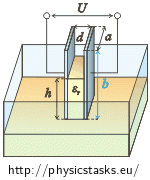
Capacitor with Oil

Task number: 2325

Plate capacitor with dimensions a = 10 cm, b = 15 cm and plate distance d = 0.2 mm touches the surface of oil with relative permitivity ε_r = 2.2 and density ρ = 760 kg m⁻³. We will connect the capacitor to DC voltage source with voltage U = 500 V. The oil then rises between the plates to height h.

a) Determine the capacity of the capacitor.

b) Determine the electric field energy increase of the capacitor and the potential gravitational energy increase of the raised part of oil. The difference in height is denoted as dh.

c) Calculate h for given stable values.

d) Determine the value of voltage that would cause the oil to fill up the whole capacitor.

• Analysis

  The capacity of the capacitor is directly proportional to the area of the plates and air permittivity and indirectly proportional to their distance before we connect them to the source.

  The oil level will rise to height h after we connect the source to the circuit. The capacity of the capacitor will increase since the permittivity of the environment with oil has increased. We can now imagine the capacitor as two parallel capacitors. One of them is fully filled with oil and the other is filled with air. The total capacity of parallel capacitors is obtained by adding up the capacities of each of the capacitors.

  Electric field energy of the capacitor is directly proportional to its capacity and the square of voltage. After we connect the capacitor to the source, its capacity increases and thus the energy of its electric field increases. We want to know how this energy changes according to capacity changes. We express the energy difference by derivative of energy with respect to capacity.

  Potential gravitational energy of oil in capacitor is directly proportional to its mass and the height of its centre of mass above the bottom edge of the capacitor. If the oil level rises then its potential gravitational energy rises as well. We can express this change of energy by the derivative of energy with respect to the height of oil surface.

  The source of voltage must work for the oil level to rise. The work done is equal to the potential gravitational energy increase and capacitor electric field energy. The work done is also directly proportional to the connected voltage and charge difference on capacitor. We can express the charge difference with capacitor capacity difference. If we have the work expressed using these two methods, we can calculate the height of the oil surface.

  If oil fills the whole capacitor, then the height of oil level is the same as the height of the capacitor. We can calculate the voltage from the equation that we formulated for oil surface height.

• a) Hint: Capacity of Capacitor

  If the capacitor is partially filled with oil, we can imagine it as two parallel capacitors. One of them is filled with oil and the other is filled with air (more detailed solution of a similar situation can be found in Capaciter partially filled with dielectric).

  How do we calculate the capacity of parallel capacitors?

• a) Solution: Capacity of Capacitor

  Before we connect the capacitor to a source, it had capacity

  $$C_0\,=\,\varepsilon_0 \,\frac{ab}{d}\,.$$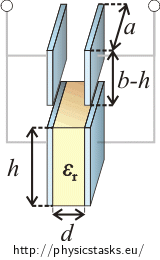

  

  After we connect the capacitor to the source, the capacitor gets partially filled with oil. We can imagine it as two parallel capacitors (see picture). Their capacity is:

  $$C_{\mathrm{vzduch}}\,=\,\varepsilon_0\, \frac{a \, \left(b-h\right)}{d}$$ $$C_{\mathrm{olej}}\,=\,\varepsilon_0\, \varepsilon_r \frac{a h}{d}$$

  The total capacity of the capacitor can be calculated as the sum of capacities of each of the capacitors; the one filled with oil and the one filled with air.

  $$C\,=\,C_{\mathrm{vzduch}} \,+\, C_{\mathrm{olej}}$$ $$C\,=\,\varepsilon_0 \,\frac{a \, \left(b-h\right)}{d} \,+\, \varepsilon_0 \,\varepsilon_r \frac{a h}{d}$$

  We factor out common terms and adjust the equation.

  $$C\,=\,\varepsilon_0 \,\frac{a }{d}\,\left( b-h\,+\, \varepsilon_r h\right)$$

  The capacitor thus has capacity

  $$C\,=\,\varepsilon_0 \frac{a }{d}\,\left( b+h\left( \varepsilon_r -1\right)\right)$$

  It is worth noticing how the capacity has changed from the original capacity C₀ of the capacitor filled with air only. We will multiply the terms to get rid of the outer parentheses so that the first term is equal to the original capacity.

  $$C\,=\,\varepsilon_0 \frac{a b }{d} +\varepsilon_0 \frac{a h\left( \varepsilon_r -1\right)}{d}\,=\,C_0 + \varepsilon_0 \frac{a h\left( \varepsilon_r -1\right)}{d}$$

  The second term is linearly dependent on height h into which the oil rises. If oil rises by dh more, the capacity of the capacitor changes in this particular term. The increase in capacity denoted as dC will be:

  $$\mathrm{d}C\,=\,\varepsilon_0 \frac{a \left( \varepsilon_r -1\right)}{d}\,\mathrm{d}h\,.\tag{1}$$

• b) Hint: Energy Change

  Capacitor electric field energy E changes with the change of the capacitor’s capacity and the potential gravitational energy E_p changes with rising surface of oil.

  Therefore we calculate the derivatives $\frac{\mathrm{d}E}{\mathrm{d}C}$ and $\frac{\mathrm{d}E_p}{\mathrm{d}h}$.

  The change of capacitor’s capacity with the change of height of oil surface has been derived in the previous section.

  Look into the note at the end of the task to see how we work with derivatives in this task.

• b) Solution: Capacitor electric field energy increase

  This relation applies for the electric field energy inside the capacitor:

  $E\,=\, \frac{1}{2}C U^2\,.$

  We want to know how this energy changes according to capacity. Therefore, we will calculate the derivative of energy with respect to capacity.

  $$\frac{\mathrm{d}E}{\mathrm{d}C}\,=\, \frac{1}{2} U^2$$

  The capacitor is connected to a stable voltage U which will therefore be considered to be a constant during derivation. We will express the energy difference.

  $$\mathrm{d}E\,=\, \frac{1}{2} U^2\mathrm{d}C$$

  We will substitute for capacity difference dC from relation (1) which we derived in the solution of part a).

  $$\mathrm{d}E\,=\, \frac{1}{2} U^2\varepsilon_0 \frac{a \left( \varepsilon_r -1\right)\mathrm{d}h}{d}$$

  If the surface of oil rises by dh, the energy of capacitor electric field changes by:

  $$\mathrm{d}E\,=\,\frac{a \varepsilon_0 \left( \varepsilon_r -1\right)U^2}{2d}\mathrm{d}h\,.$$

• b) Solution: Potential Gravitational Energy Difference

  We will calculate the potential gravitational energy using the following relation

  $$E_p\,=\,mgH\,.$$

  Attention! H is the height of the centre of mass of the object! The centre of mass is in height $\frac{h}{2}$ in our case and so the following applies for potential energy:

  $$E_p\,=\,mg\,\frac{h}{2}\,=\,V \varrho g \,\frac{h}{2}\,,\tag{*}$$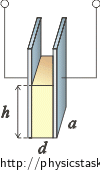

  

  where V is the volume of the oil in the capacitor.

  We will calculate oil volume V = adh as the picture shows and we will substitute into relation (*).

  $$E_p\,=\,adh \varrho g \,\frac{h}{2}\,=\,\frac{1}{2}ad \varrho g \,h^2$$

  We want to know how this potential gravitational energy changes according to the oil height difference. We will therefore calculate its derivative with respect to height.

  $$\frac{\mathrm{d}E_p}{\mathrm{d}h}\,=\,ad \varrho g \,h$$

  The difference of potential gravitational energy equals:

  $$\mathrm{d}E_p\,=\,ad \varrho gh\,\mathrm{d}h \,.$$

• c) Hint: Oil Surface Height Calculation

  We can calculate the oil height from the following equation for work done by voltage source:

  $$\mathrm{d}W\,=\,U \mathrm{d}Q$$

  Think about how the work done affects capacitor energy.

• c) Solution: Oil Level Height h Calculation

  We can calculate the oil surface height from work done by voltage source when it is raising the oil surface.

  

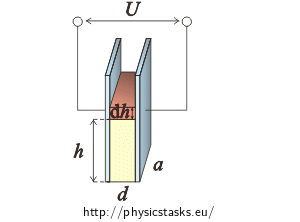
  Source gives out constant voltage U and the oil surface is at height h. If we wanted the oil surface to rise a little bit more by dh, the source must do work dW.

   

  Since the voltage on the capacitor is constant, the work done is equal to

  $$\mathrm{d}W\,=\,U \,\mathrm{d}Q\,.$$

  The difference of charge with constant voltage can be expressed using capacitor capacity difference dQ = U dC.

  $$\mathrm{d}W\,=\,U^2 \,\mathrm{d}C\,.\tag{2}$$

  If the source does this work, the oil level rises by dh. This work will cause energy change. Since the oil level rose by dh, its potential gravitational energy rose by dE_p. The capacitor’s capacity changed as well and thus the capacitor’s energy rose by dE.

  $$\mathrm{d}W\,=\,\mathrm{d}E_p\,+\,\mathrm{d}E\,\tag{3}$$

  Now we will compare both relations (2) and (3) for work calculation.

  $$U^2 \,\mathrm{d}C\,=\,\mathrm{d}E_p\,+\,\mathrm{d}E$$

  We have expressed all terms in the previous sections and now we will substitute them in.

  $$\frac{a \varepsilon_0 \left( \varepsilon_r -1\right)U^2}{d}\mathrm{d}h\,=\,\frac{a \varepsilon_0 \left( \varepsilon_r -1\right)U^2}{2d}\mathrm{d}h \,+\, ad \varrho gh\,\mathrm{d}h$$

  We will adjust the relation to express h. First we subtract the fractions

  $$\frac{a \varepsilon_0 \left( \varepsilon_r -1\right)U^2}{2d}\mathrm{d}h\,=\, ad \varrho gh\,\mathrm{d}h\,.\tag{**}$$

  Then we will divide by a and dh

  $$\frac{ \varepsilon_0 \left( \varepsilon_r -1\right)U^2}{2d}\,=\, d \varrho gh$$

  and we will express height h to which the oil rose in the capacitor.

  $$h\,\, =\, \frac{ \varepsilon_0 \left( \varepsilon_r -1\right)U^2}{2 \varrho gd^2}$$

• d) Hint: Voltage Calculation

  Once oil fills the whole capacitor, what will the height of oil level be?

  Use the general result derived in the previous sectrion for calculation.

• d) Solution: Voltage Calculation

  In section Oil Level Height Calculation, we have expressed height h to which the oil rises with the given voltage.

  $$h\,\,=\, \frac{ \varepsilon_0 \left( \varepsilon_r -1\right)U^2}{2 \varrho gd^2}$$

  We will use this result for voltage U₁ calculation. The voltage is needed for the oil to fill the whole capacitor.

  If the oil fills the whole capacitor, its height h will be equal to the height of the capacitor b. Therefore, the following applies:

  

  $$h\,\,=\,b\,=\, \frac{ \varepsilon_0 \left( \varepsilon_r -1\right)U^2_1}{2 \varrho gd^2}\,.$$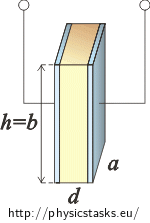

  Now, we just need to express voltage U₁.

  $$U^2_1\,=\, \frac{2 b\varrho gd^2}{ \varepsilon_0 \left( \varepsilon_r -1\right)}$$ $$U_1\,=\, \sqrt{\frac{2 b\varrho gd^2}{ \varepsilon_0 \left( \varepsilon_r -1\right)}}$$

  We have to connect the capacitor to voltage:

  $$U_1\,=\, \sqrt{\frac{2 b\varrho g}{ \varepsilon_0 \left( \varepsilon_r -1\right)}}\,d\,.$$

• List of Known Information and Numerical Calculation

  U = 500 V	h = ? (m)
  a = 10 cm = 0.1 m	U1 = ? (V)
  b = 15 cm = 0.15 m
  d = 0.2 mm = 0.2·10−3 m	From tables:
  εr = 2.2	ε0 = 8.85·10−12  C2N−1m−2
  ρ = 760 kg m−3	g = 9.8 m s−2

  ---

  $$h\,\, =\, \frac{ \varepsilon_0 \left( \varepsilon_r -1\right)U^2}{2 \varrho gd^2}\, =\, \frac{ 8.85 {\cdot} 10^{-12}\cdot \left( 2.2 -1\right)\cdot500^2}{2 {\cdot} 760 \cdot9.8\cdot \left(0.2 {\cdot} 10^{-3}\right)^2}\,\mathrm{m}\,\dot=\,4.46 {\cdot} 10^{-3}\,\mathrm{m}$$ $$h\,\dot=\,4{,}46 \,\mathrm{mm}$$ $$U_1\,=\, \sqrt{\frac{2 b\varrho g}{ \varepsilon_0 \left( \varepsilon_r -1\right)}}\,d\,=\, \sqrt{\frac{2 {\cdot} 0.15 {\cdot} 760 \cdot9.8}{ 8.85 {\cdot} 10^{-12}\cdot \left( 2.2 -1\right)}}\cdot 0.2 {\cdot} 10^{-3}\,\mathrm{V}$$ $$U_1\,\dot=\, 2\,901\,\mathrm{V}\,\dot=\, 2.9\,\mathrm{kV}$$

• Answer

  The capacitor has capacity of $C\,=\,\varepsilon_0 \frac{a }{d}\left( b+h\left( \varepsilon_r -1\right)\right)\,.$

  If the oil level rises by dh, the capacitor electric field energy changes by

  $$\mathrm{d}E\,=\,\frac{a \varepsilon_0 \left( \varepsilon_r -1\right)U^2}{2d}\mathrm{d}h$$

  and the potential gravitational energy of the risen part of oil rises by

  $$\mathrm{d}E_p\,=\,ad \varrho gh\,\mathrm{d}h \,.$$

  For the given values, the oil will rise to height

  $$h\,\,=\, \frac{ \varepsilon_0 \left( \varepsilon_r -1\right)U^2}{2 \varrho gd^2}\, \dot=\,4.46 \,\mathrm{mm}\,.$$

  For the oil to cover the whole capacitor, we need to connect it to voltage of

  $$U\,=\, \sqrt{\frac{2 b\varrho g}{ \varepsilon_0 \left( \varepsilon_r -1\right)}}\,d\,\dot=\,2.9 \,\mathrm{kV}\,.$$

• Note: Derivatives and Fractions

  We often consider derivatives to be fractions in this task. This has to be mathematicaly proven but we will show only the „physical“ thought process behind it and why it is OK.

  We write, for example, the difference of potential gravitational energy at highschool as the following:

  $$\mathrm{\Delta} E_p\,=\, m g \, \mathrm{\Delta} h$$ $$\frac{\mathrm{\Delta} E_p }{\mathrm{\Delta} h\,}=\, m g \,$$

  If the increase Δh is very small (which means that it will be zero in its limit), then this applies:

  $$\lim_{\mathrm{\Delta}h \rightarrow 0}\, \frac{\mathrm{\Delta} E_p }{\mathrm{\Delta} h\,}=\, \frac{\mathrm{d} E_p }{\mathrm{d} h\, }$$

  Therefore, if we work with small increments, we can „compare derivatives to quotients“

  $$\frac{\mathrm{\Delta} E_p }{\mathrm{\Delta} h\,}\dot=\, \frac{\mathrm{d} E_p }{\mathrm{d} h\,}$$

  and work with the derivatives like with fractions

  $$\frac{\mathrm{d} E_p }{\mathrm{d} h\,}=\, m g \,$$ $$\mathrm{d} E_p\,=\, m g \, \mathrm{d} h$$

• Link to Similar Tasks

  In task Dielectric lift you can find how the task would be solved had the capacitor been cylindrical.

  You can find the way how to calculate the capacity of a cylindrical capacitor with dielectric in task Capaciter partially filled with dielectric.

• Other Ways of Oil Surface Height Calculation

  We could also calculate the oil surface height from the equation of electric and gravitational force like in task Dielectric lift

  .

  The result would be the same. We can see that from relation (**) from section Surface Height h Calculation.

  $$\frac{a \varepsilon_0 \left( \varepsilon_r -1\right)U^2}{2d}\mathrm{d}h\,=\, ad \varrho gh\,\mathrm{d}h\tag{**}$$

  After dividing by dh.

  $$\frac{a \varepsilon_0 \left( \varepsilon_r -1\right)U^2}{2d}\,=\, ad \varrho gh$$

  The gravitational force is on the right side of the equation. Since the mass of oil ism = Vρ = adhρ, the gravitational force is equal to:

  $$F_G\,=\,mg\,=\,adh \varrho g$$

  The electric force is on the left side of the equation. The following has been derived in task Dielectric lift:

  $$F\,=\,\frac{1}{2}U^2\, \frac{\mathrm{d}C}{\mathrm{d}h}\,.$$

  In our case after substituting the capacity:

  $$F\,=\,\frac{a \varepsilon_0 \left( \varepsilon_r -1\right)U^2}{2d}\,.$$

  This applies in general:

  The components of force can be obtained by derivation of the potential energy with respect to the according coordinate.

  $$F_x\,=\, - \frac{\mathrm{d}E_p}{\mathrm{d}x}$$

  The force vector is therefore equal to

  $$\vec{F}\,=\, - \mathrm{grad}E_p\,.$$