Mutual Interaction of Two Dipoles
Task number: 1536
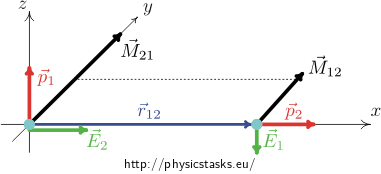
Two ideal dipoles \(\vec p_1\), \(\vec p_2\) are placed at a distance r as shown in the figure.
What is the moment of force exerted by the first dipole on the second dipole? What is the moment of force exerted by the second dipole on the first one?
Do not expect the moments of forces to be of the same size and opposite direction. This is a different case. The principle of action and reaction applies on forces, not on the moments of forces.
Hint 1
Ideal dipole \(\vec p\) ocated at the origin and generating electric field at point \(\vec r\) is determined by the expression
\[{\vec E}({\vec r}) = \frac{1}{4\pi\varepsilon_0}\left(\frac{3({\vec p}\cdot {\vec r}){\vec r}}{r^5}-\frac{{\vec p}}{r^3}\right)\]Hint 2
Derive or find a relation for a moment of force exerting on a dipole placed in an electric field.
Hint 3
Use the relation stated in the section Hint 2 describing the moment of force exerting on a dipole in an electric field. Remember that the following needs to be substituted into the relation describing the moment of force exerting on the first dipole:
- Dipole moment of the first dipole
- Expression describing the intensity of electric field generated by the second dipole in the place of the first dipole
Similarly, we substitute into the relation describing the moment of force exerting on the second dipole
- Dipole moment of the second dipole
- Expression describing the intensity of electric field generated by the first dipole in the place of the second dipole
Hint 4
After substituting into the equation for the moment of force (see Hint 2 and Hint 3), note that
in the case of the first dipole the dipole moment \(\vec p_1\) 1 is perpendicular to the vector joining the first and the second dipole \(\vec r_{12}\) (therefore their scalar product is zero)
in the case of the second dipole the dipole moment \(\vec p_2\) is parallel to the vector connecting the second and first dipole \(\vec r_{21}\) and they have opposite direction. Thus we can replace one with the other, for example:
\[\frac{\vec p_2}{p_2} = -\frac{\vec r_{21}}{r_{21}}\]
(When we divide a vector by its magnitude, we obtain a unit vector; the minus sign corresponds to an opposite orientation of the vector.)
Analysis
Both dipoles are considered to be ideal. An ideal dipole placed at the origin of the coordinate system generates in its neighbourhood an electric field with electric intensity
\[{\vec E}({\vec r}) = \frac{1}{4\pi\varepsilon_0}\left(\frac{3({\vec p}\cdot {\vec r}){\vec r}}{r^5}-\frac{{\vec p}}{r^3}\right)\]This field exerts on the second dipole. Let us derive that a moment of force \(\vec M\) cting on a dipole with a dipole moment \(\vec p\) placed in an electric field of intensity \(\vec E\) is
\[{\vec M} = {\vec r}\times {\vec F} = {\vec r}\times {q\vec E} = {q\vec r}\times {\vec E} = {\vec p}\times {\vec E}\]Now we need to combine the relations, adjust them and interpret the result.
To do this, we use the arrangement of the dipoles!
Solution
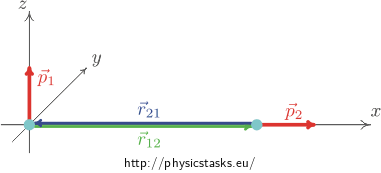
We place the dipoles in such a way, so that the dipole \(\vec p_1\) is located at the point of the origin of the coordinate system and its direction is the same as the direction of the z – axis. The dipole \(\vec p_2\) is placed on the x - axis at a distance r and its direction is the same as the x - axis direction.(See the figure bellow).
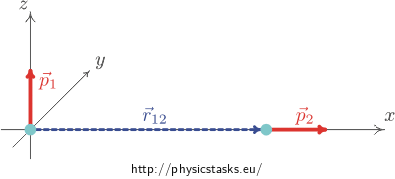
How does the first dipole exert on the second dipole?
The vector \(\vec r_{12}\) is a vector connecting the two dipoles and pointing from the first dipole to the second dipole. The vector \(\vec r_{21} = -\vec r_{12}\) is a vector pointing from the second dipole to the first dipole. Obviously, the magnitude of the two vectors is the same and is equal to the distance r between the dipoles.
Then the dipole \(\vec p_1\) exerts on the dipole \(\vec p_2\) by a moment of force \(\vec M_{12}\) and it applies
\[\vec M_{12} = \vec p_2 \times \vec E_1\]where \(\vec E_1\) denotes the intensity of electric field that is generated by the first dipole in the place of the second dipole. The electric intensity \(\vec E_1\) is
\[{\vec E_1}({\vec r_{12}}) = \frac{1}{4\pi\varepsilon_0}\left(\frac{3({\vec p_1}\cdot {\vec r_{12}}){\vec r_{12}}}{r_{12}^5}-\frac{{\vec p_1}}{r_{12}^3}\right).\]The vector \(\vec p_1\) is perpendicular to the vector \(\vec r_{12}\), the scalar product in the first component is zero, and we obtain
\[{\vec E_1}({\vec r_{12}}) = -\frac{1}{4\pi\varepsilon_0}\frac{{\vec p_1}}{r_{12}^3}\]The vectors \(\vec E_1\) and \(\vec p_1\)are of an opposite orientation; the vector \(\vec E_1\) points vertically downwards in the negative direction of the z - axis.
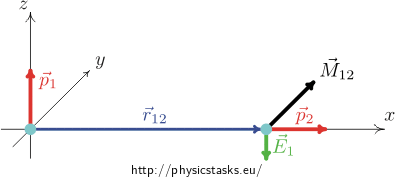
Using the right-hand rule we can see that the direction of \(\vec M_{12}\) is in the positive direction of the y - axis and has a magnitude
\[M_{12} = p_2\cdot \frac{p_1}{4\pi\varepsilon_0 r_{12}^3} = \frac{p_1p_2}{4\pi\varepsilon_0r^3}\]How does the second dipole exert on the first dipole?
On the other hand, the dipole \(\vec p_2\) exerts on the dipole \(\vec p_1\) by a moment of force \(\vec M_{21}\) and it applies
\[\vec M_{21} = \vec p_1 \times \vec E_2\]where
\[{\vec E_2}({\vec r_{21}}) = \frac{1}{4\pi\varepsilon_0}\left(\frac{3({\vec p_2}\cdot {\vec r_{21}}){\vec r_{21}}}{r_{21}^5}-\frac{{\vec p_2}}{r_{21}^3}\right)\]and because the vectors \(\vec p_2\) and \(\vec r_{21}\) have the same direction and opposite orientation, the following applies
\[\vec p_2 \cdot \vec r_{21} = -p_2r_{21}\]and
\[\vec p_2 = p_2\, \left(\frac{-\vec r_{21}}{r_{21}}\right), \qquad {\rm nebo} \qquad -p_2\vec r_{21} = r_{21}\vec p_2\]Using these relations, we obtain
\[{\vec{E_2}}({\vec{r_{21}}}) = \frac{1}{4\pi\varepsilon_0}\left(-\frac{3p_2r_{21}{\vec r_{21}}}{r_{21}^5}-\frac{p_2}{r_{21}^3}\,\left(\frac{-\vec r_{21}}{r_{21}}\right)\right)\]and thanks to the previous equality \(-p_2\vec r_{21} = r_{21}\vec p_2\) we can adjust the expression
\[{\vec E_2}({\vec r_{21}}) = \frac{1}{4\pi\varepsilon_0}\frac{2\vec p_2}{r_{21}^3}\]From here it is clear that the vector \(\vec E_2\) points to the right, i.e. in the positive direction of the x - axis and has a magnitude
\[E_2 = \frac{2p_2}{4\pi\varepsilon_0 r^3}\]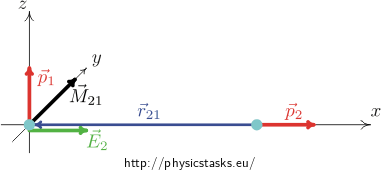
Therefore, using the right–hand rule, we can see that the vector \(\vec M_{21}\) points in the positive direction of y - axis and its magnitude is
\[M_{21} = \frac{2p_1p_2}{4\pi\varepsilon_0 r^3}\]Note that both moments have the same direction and orientation and different magnitude. This is not in conflict with the principle of action and reaction; the principle applies on forces; moreover, the situation is far from symmetric – the vector connecting the two dipoles is parallel to the dipole moment of one dipole, while it is perpendicular to the dipole moment of the other dipole.
Answer
The first dipole exerts on the second dipole by the moment of force \(\vec M_{12}\), the moment points in the positive direction of the y - axis and has a magnitude
\[M_{12} = \frac{p_1p_2}{4\pi\varepsilon_0 r^3}\]The second dipole exerts on the first dipole by the moment of force \(\vec M_{21}\), moment points in the positive direction of the y-axis and has a magnitude
\[M_{21} = \frac{2p_1p_2}{4\pi\varepsilon_0 r^3}\]