Field of Charged Plane Solved in Many Ways
Task number: 2318
Calculate the electric intensity around homogeneously charged infinite plane (denote the surface charge density as \(\sigma\)):
a) by direct integration using polar coordinates,
b) by direct integration where the plane is considered as “many lines” next to each other,
c) by integrating the potential and then using the relation between the electric intensity and potential,
d) by using the Gauss theorem of electrostatics.
Note: Assume that the plane is charged positively.
a) Hint – direct integration using polar coordinates
Positive point charge Q causes electric field with intensity of
\[E=\frac{1}{4\pi\epsilon_0} \frac{Q}{r^2}\]in distance r. The vector of intensity \(\vec{E}\) points away from the charge if charge Q is positive. In the opposite case, the vector points towards the charge.
Think through how to use this knowledge in this task.
a) Comment – direct integration using polar coordinates
We will draw the whole situation into the Cartesian coordinate system for clarity. We will also draw cylindrical coordinates \(\rho, \alpha, z\) into the picture.
Note: r, \(\varphi\), z. are usuJly used for cylindrical coordinates but since \(\varphi\) already denotes the electric potential that will be used later, it is necessary to denote the angle differently. The distance between a point and the origin of the used coordinate system is usually denoted as r but we will use \(\rho\) since r already appears in the relation for intensity of a point charge. For short, \(\rho\) is the distance between a point and the origin of the coordinate system and r is the distance between a point and the point where we calculate the intensity of the electric field at (point lying on the z-axis).
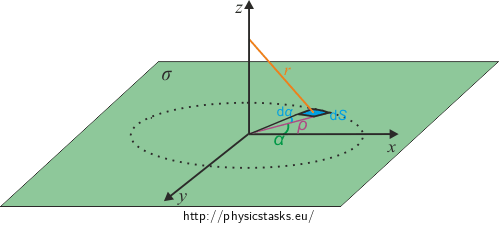
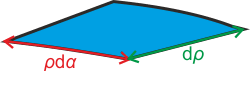
We will separate the plane into small (infinitesimal) areas that will behave like point charges according to the hint.
a) Solution – Direct Integration Using Polar Coordinates
Point charge Q creates an electric field of intensity
\[{E}=\frac{1}{4\pi\epsilon_0} \frac{Q}{r^2}.\]at distance r. The size of the electric intensity caused by an infinitesimally small surface dS is
\[\textrm{d}{E}=\frac{1}{4\pi\epsilon_0}\frac{\mathrm{d}Q}{r^2}.\]If the surface is charged with surface density \(\sigma\), then the charge on an infinitesimally small part of the surface \(\textrm{d}S\) is
\[\textrm{d}Q = {\sigma} {\textrm{d}S},\]where \(\textrm{d}S=\rho\,\textrm{d}\alpha\,\textrm{d}\rho\) (see previous section).
Thus we obtain
\[\textrm{d}Q=\sigma \rho \textrm{d}\alpha\textrm{d}\rho\]and therefore
\[\textrm{d}{E}=\frac{1}{4\pi\epsilon_0}\frac{\sigma \rho\textrm{d}\alpha\textrm{d}\rho}{r^2}.\tag{1}\]Now we will focus on the direction of the intensity. We know that the surface is infinite and that it is homogenously charged.
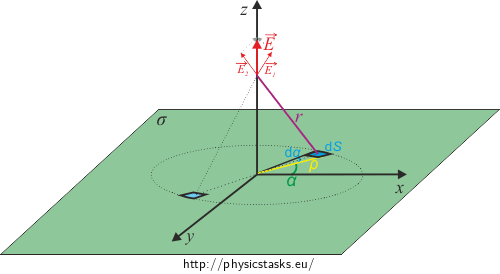
It is obvious from the picture that the direction of the total intensity of the electric field will have the direction of the z-axis since the x component of electric intensity of a small area will cancel out with an area that lies in central symmetry with respect to the origin. The y component will also cancel out in the same manner.
We will denote angle \(\omega\) and electric intensity in the direction of the z-axis from a single small area into the picture. In other words: we will express its z component:
\[E_\mathrm{z}=E \cos \omega.\tag{2}\]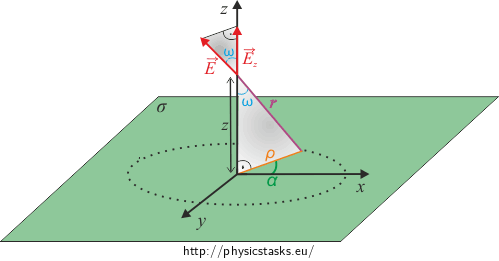
We obtain the following from the gray right-angled triangle:
\[\cos \omega = \frac {z}{r}\]and the Pythagoras theorem adds the following
\[r=\sqrt{\rho^2 + z^2},\]which yields
\[\cos \omega = \frac {z}{\sqrt{\rho^2 + z^2}}.\tag{3}\]By connecting (1),(2) and (3), we obtain
\[\textrm{d}{E_\mathrm{z}}=\frac{1}{4\pi\epsilon_0}\frac{\sigma\rho \textrm{d}\alpha\textrm{d}\rho}{\rho^2 + z^2}\frac {z}{\sqrt{\rho^2 + z^2}}=\frac {\sigma z}{4\pi\epsilon_0} \frac {\rho} {(\rho^2 + z^2)^{3/2}} \textrm{d}\alpha \textrm{d}\rho,\]which we will integrate across the whole plane, i.e. we will integrate across \(\rho\) and \(\alpha\), \(\rho\) reaches values from \(0\) to \(\infty\) and \(\alpha\) reaches values from \(0\) to \(2\pi\):
\[E_\mathrm{z} = \int_0^\infty \int_0^{2\pi} \frac {\sigma z}{4\pi\epsilon_0} \frac {\rho} {(\rho^2 + z^2)^{3/2}} \textrm{d}\alpha \textrm{d}\rho.\]\(\sigma\) and z are independent from the integrated variables \( \rho \) and \(\alpha,\) and so we can factor them out along with other constants:
\[E_\mathrm{z} = \frac {\sigma z}{4\pi\epsilon_0} \int_0^\infty \int_0^{2\pi} \frac {\rho} {(\rho^2 + z^2)^{3/2}}\textrm{d}\alpha \textrm{d}\rho .\]Now we will integrate the term across \(\alpha\) since \(\alpha\) does not occur in the term, it is like integrating a constant:
\[E_\mathrm{z} =\frac {\sigma z}{4\pi\epsilon_0} 2\pi \int_0^\infty \frac {\rho} {(\rho^2 + z^2)^{3/2}}\textrm{d}\rho,\] \[E_\mathrm{z} = \frac {\sigma z}{2\epsilon_0} \int_0^\infty \frac {\rho} {(\rho^2 + z^2)^{3/2}}\textrm{d}\rho.\]What remains is the integral across \(\rho\) which will be solved using substitution:
\[a = \rho^2 + z^2,\] \[\textrm{d}a = 2\rho\textrm{d}\rho, \]We will recalculate the limits:
\[\rho = 0 \Rightarrow a = z^2;\qquad \rho = \infty \Rightarrow a = \infty, \]and we will substitute into the original integral:
\[E_\mathrm{z} = \frac {\sigma z}{2\epsilon_0} \int_{z^2}^{\infty} \frac {1} {2a^{3/2}}\textrm{d}a,\] \[E_\mathrm{z} = \frac {\sigma z}{4\epsilon_0} \int_{z^2}^{\infty} {a^{-3/2}}\textrm{d}a,\] \[E_\mathrm{z} = \frac {\sigma z}{4\epsilon_0} \left[-2a^{-1/2}\right]_{z^2}^\infty, \] \[E_\mathrm{z} = - 0 + \frac {\sigma}{2\epsilon_0}\frac{z}{|z|}=\frac {\sigma}{2\epsilon_0}\frac{z}{|z|}. \]The last fraction in the result is a unit vector that is parallel with the z-axis and which directs the direction of the electric intensity. If the plane were charged positively, then the electric intensity would point in the positive direction of the z-axis if we are above the plane and the electric intensity would point in the negative direction of the z-axis if we are below the plane.
b) Hint – Direct Integration Using “many lines“
A homogenously charged line with linear charge density \(\lambda\) creates a field around itself (see Field of Charged Line) with intensity of
\[E = \frac {\lambda}{2\pi\epsilon_0z.}\]The electric intensity points perpendicularly away from the wire and its direction is shown in the next picture.
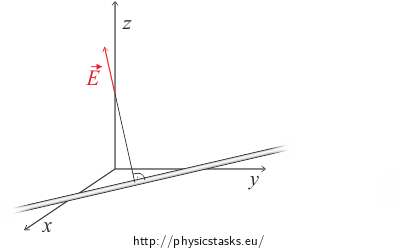
Think about how we could use this knowledge.
b) Analysis – Direct Integration Using “Many Lines“
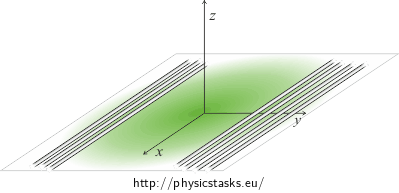
We will separate the plane into infinitely many parallel lines. The total intensity can be obtained by “adding up“ (or rather by integrating) the components from all of the lines.
b) Solution – Direct Integration Using “Many Lines“
Let us choose the Cartesian coordinate system in such a way so that the charged plane lies in the xy-plane and we search for the electric intensity on the z-axis.
We know that a homogenously charged line with linear density \(\lambda\) creates electric field of
\[E=\frac{\lambda}{2\pi\epsilon_0r}\tag{4}\]at distance r. See Field of Charged Line.
Linear density \(\lambda\) is related to area density \(\sigma\) by the following relation
\[\lambda = \sigma\ \mathrm{d}y.\]If we imagine the plane as many parallel lines then every addition of electric intensity from every line is
\[dE=\frac{\sigma}{2\pi\epsilon_0r}\textrm{d}y.\]Think about the symmetry of the task.
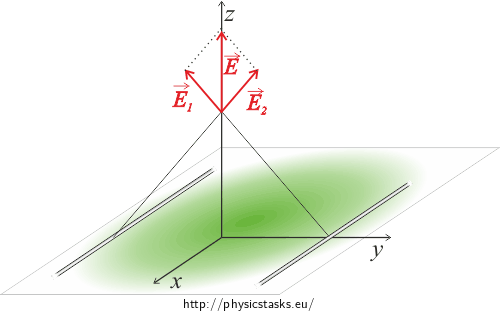
We can see from the picture that for every line we choose there is a line that is symmetrical to it across the x-axis we chose. All contributions have therefore zero x component. Contributions to the y component of the electric intensity will cancel out because of symmetry as well and we will be left with the z component only.
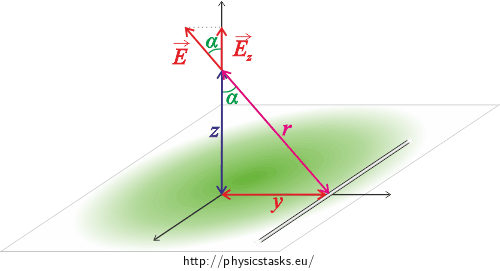
We will mark angle \(\alpha\) into the picture and the electric intensity from one of the lines. It will point in the direction of the z-axis, i.e. we will express its z component:
\[E_\mathrm{z} = \cos \alpha \ E.\tag{5}\]We obtain the following from right-angled triangle similarity:
\[\cos \alpha = \frac {z}{r},\]where \(r=\sqrt{z^2 + y^2}.\)
By connecting (4) and (5), we receive:
\[\textrm {d}E_\mathrm{z} = \frac {z}{\sqrt{z^2+y^2}}\frac{\sigma}{2\pi\epsilon_0\sqrt{z^2+y^2}}\textrm{d}y,\]which we will integrate across all lines, i.e. we will integrate across \(y\):
\[E_\mathrm{z} = \int_{-\infty}^{\infty}\frac{\sigma z}{2\pi\epsilon_0{(z^2+y^2)}}\textrm{d}y,\] \[E_\mathrm{z} = \frac{\sigma z}{2\pi\epsilon_0}\int_{-\infty}^{\infty}\frac{1}{z^2+y^2}\textrm{d}y.\]This integral leads to the arcus tangent function (the inverse function to the tangent function). Let us remind ourselves of the derivation of the arcus tangent function:
\[\frac{\mathrm{d}\ \mathrm{arctg}\, x}{\mathrm{d}x}=\frac{1}{1+x^2}\]We will adjust the integral to a form such that we can use this equation. We will factor \(z^2\) from the denominator:
\[E_\mathrm{z} = \frac{\sigma }{2\pi\epsilon_0 z} \int_{-\infty}^{\infty}\frac{1}{1+(\frac{y}{z})^2}\textrm{d}y,\] \[E_\mathrm{z} = \frac{\sigma }{2\pi\epsilon_0 z} \Big[z\arctan\frac{y}{z}\Big]_{-\infty}^{\infty}.\]We know this about the arcus tangent function
\[\lim_{y\rightarrow \pm\infty}\arctan{\frac{y}{z}}=\pm\frac{\pi}{2} \mathrm{sgn}\ z=\pm\frac{\pi}{2} \frac {z}{|z|},\]which yields the following after substitution
\[E_\mathrm{z} = \frac{\sigma }{2\pi\epsilon_0 z}(z \frac {|z|}{z} \frac{\pi}{2} + z \frac {|z|}{z} \frac{\pi}{2}),\] \[E_\mathrm{z} = \frac{\sigma }{2\epsilon_0} \frac {|z|}{z}.\]Note: Function \(\mathrm{sgn}\ x\), called sign function, is a function that returns the sign of the variable. So if \(x>0\) then \(\mathrm{sgn}\ x=1\), if \(0>x\) then \(\mathrm{sgn}\ x=-1\), and if \(x=0\) then \(\mathrm{sgn}\ x = \mathrm{sgn}\ 0=0\).
c) Hint – intensity from potential
One particular equation containing the mathematical operator gradient gives a relation between potential and electric intensity.
Try to recall or find this particular equation and the relation we talk about. Remind yourselves what gradient is and how to calculate it (in Cartesian coordinates).
Next try to find what is the potential above the equally charged plane with area density of \(\sigma\).
c) Hint – Relation for Potential Around Charged Plane
Potential of an electrical field of a homogenously charged plane has the following form (tato úloha nemá překlad a jediná úloha, která je přeložená a zabývá se potenciálem v okolí nabité roviny, je http://physicstasks.eu/1533/field-of-thick-charged-plate s tím, že tam mají ale jiný výsledek (-ρz^2/2ε_0))
\[\varphi(z) = - \frac {\sigma}{2\epsilon_0} |z|.\]c) Solution – Intensity From Potential
Electric intensity and potential are connected through the following equation
\[\vec{E} = - \text{grad} \varphi = -\left(\frac{\partial{\varphi}}{\partial {x}},\frac{\partial{\varphi}}{\partial {y}},\frac{\partial{\varphi}}{\partial {z}}\right).\]The right side of the equation says how the gradient of a scalar function is calculated in the Cartesian coordinate system:
\[\varphi(x,y,z) = - \frac {\sigma}{2\epsilon_0} |z|.\]Note: In this case, we know the potential dependence on all coordinates (we have it expressed at all points) so we can calculate all components of the electric intensity. We would have to advance differently on the axis of a homogenously charged hoop (see task Electric field on the axis of a hoop) even though it might seem like a similar case.
The calculation of the first two components of the electric intensity is simple:
\[\frac{\partial{\varphi}}{\partial {x}}=0,\] \[\frac{\partial{\varphi}}{\partial {y}}=0.\]We will separate the calculation of the z component into two parts because of the derivative of the absolute value with respect to z. We will calculate the derivative once for \(z>0\) and once for \(z<0\).
The potential will have the following form for \(z>0\)
\[\varphi(x,y,z) = - \frac {\sigma}{2\epsilon_0} z,\]and we will receive after derivation:
\[\frac{\partial{\varphi}}{\partial {z}}= -\frac {\sigma}{2\epsilon_0} \qquad \text{pro}\ \forall z>0.\]The potential will have the following form for \(z<0\)
\[\varphi(x,y,z) = - \frac {\sigma}{2\epsilon_0} (-z) = \frac {\sigma}{2\epsilon_0} z,\]and we will receive after derivation:
\[\frac{\partial{\varphi}}{\partial {z}}= \frac {\sigma}{2\epsilon_0} \qquad \text{pro}\ \forall z<0.\]Both results can be connected and written as one:
\[\frac{\partial{\varphi}}{\partial {z}}= -\frac {\sigma}{2\epsilon_0}\frac{z}{|z|} \qquad \ \forall z \in \mathbb{R} \setminus \text{{0}}.\]Thus we receive the relation for electric intensity
\[\vec{E} = \left(0, 0, \frac {\sigma}{2\epsilon_0}\frac{z}{|z|} \right), \qquad \forall z \in \mathbb{R} \setminus \text{{0}}. \]The last term in the relation is, like in a) and b), a unit vector that is parallel with the z-axis. It determines the direction of the electric intensity. If the plane were to be charged positively, then the electric intensity would point towards the positive direction of the z-axis while above the plane and it would point towards the negative direction of the z-axis while bellow the plane.
d) Link – Using Gauss Theorem of Electrostatics
Electric intensity calculation around homogenously charged plane using the Gauss theorem of electrostatics can be found in task Field of Evenly Charged Plane.
Answer
The vector of electric intensity has the following form around infinite homogenously charged plane:
\[\vec{E}=\left(0\ ; 0\ ; \frac {\sigma}{2\epsilon_0}\frac{z}{|z|} \right).\]