Collection of Solved Problems in Physics

Capaciter partially filled with dielectric

Task number: 2168

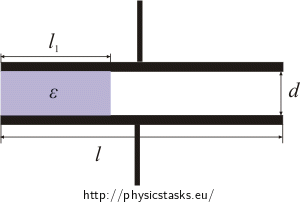
Find the resulting capacity of a plate capacitor, if the space between the plates of area S is filled with dielectric with permittivity ε according to the picture.

• Hint: How to begin

  Capacitor that is filled with dielectric this way can be replaced with two parallel capacitors. One will be filled with air and one will be completely filled with dielectric.

• Hint: Capacity of capacitor

  The capacity of parallel capacitors is the sum of each one’s capacity.

• Analysis

  Plate capacitor that is filled with dielectric this way can be replaced with two parallel capacitors. One will be filled with air and one will be completely filled with dielectric.

  The total capacity of parallel capacitors is equal to the sum of each one’s capacity.

  Capacity of a plate capacitor is indirectly dependent on the distance of the plates and directly dependent on the plates’ areas and the permittivity of the environment that is between the plates.

  The only thing, that is left to be found, are the areas of the plates of both capacitors. We will use the fact, that we know the combined area of the capacitors, and the ratio in which the capacitor was divided into two.

• Solution

  We will replace the plate capacitor with two that are parallel. One will be filled with dielectric l₁ wide, the other will be filled with air and l−l₁ wide.

  

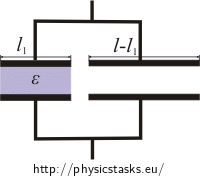
  The total capacity is then given by the sum of each capacitor’s capacity:

  \[C\,=\,C_1+C_2\tag{1}\]

  The capacity of a plate capacitor is given by:

  \[C\,=\, \epsilon \frac{S}{d}\,=\,\epsilon_0 \epsilon_r \frac{S}{d}\]

  Equations given for the capacities of our capacitors are:

  \[C_1\,=\, \epsilon_0 \epsilon_r\frac{S_1 }{d}\tag{2}\] \[C_2\,=\,\epsilon_0 \frac{S_2 }{d}\tag{3}\]

  Now, we will determine the areas S₁ and S₂ using the lengths l, l₁ and the total area of the capacitors S.

  The total area of the capacitor is:

  \[ S\,=\,lx\,\,\Rightarrow\,\,x\,=\,\frac{S}{l}\,,\tag{*}\]

  where x is the width of the capacitor.

  Areas S₁ and S₂ can be determined likewise S₁ = l₁x and S₂ = (l-l₁)x.

  If we then replace x from the equation (*), we will get the areas of both capacitors, which are needed.

  \[S_1\,=\,\frac{l_1}{l}S\] \[S_2\,=\,\frac{l-l_1}{l}S\]

  Now we just need to put S₁ and S₂ into equations for capacities C₁ and C₂ (equation (2) and (3)) and then put everything into equation (1) for the total capacity.

  \[C\,=\, \epsilon_0 \epsilon_r \frac{l_1 S}{dl} +\epsilon_0 \frac{\left(l-l_1\right) S}{dl}\]

  We will factor out \(\frac{\epsilon_0 S}{dl}\):

  \[C\,=\, \frac{\epsilon_0 S}{dl} \left( \epsilon_r l_1+l-l_1\right)\]

  Now we can factor l₁ out from the parentheses and we will get the equation for the total capacity of the capacitor C.

  \[C\,=\, \frac{\epsilon_0 S}{dl} \left(l_1 \left(\epsilon_r -1\right)+l\right)\]

• Answer

  The total capacity of the capacitor is given by:

  \[C\,=\, \frac{\epsilon_0 S}{dl} \left(l_1 \left(\epsilon_r -1\right)+l\right)\,.\]

• Dielectric put in another way

  Think about how to solve this problem, if the dielectric were put in an other way (see picture).

  

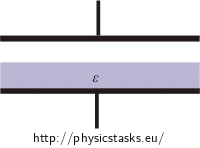
  Should the capacitor be filled with delectric the way the picture shows, we would split it again into two (the air-filled one and the one filled with dielectric). In this case the capacitors would be connected in series.