Collection of Solved Problems in Physics

Magnetic Force between Two Wires Carrying Current

Task number: 2112

• Hint

  Draw the magnetic field which the wire with current creates around itself.

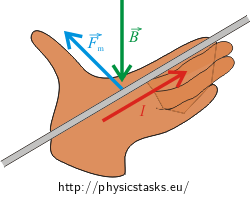
  Since one of the wires is located in the magnetic field of the other one, it will be influenced by the magnetic force whose magnitude is proportional to the magnitude of the magnetic field caused by the second wire, to the magnitude of the current in the first wire, and to the length of the wire. The direction of this force can be determined by the Fleming's left-hand rule.

• Hint Solution: Magnetic field of a wire carrying current

  A magnetic field \(\vec{B}\) arises around a wire carrying electric current. Magnetic field lines of the vector field \(\vec{B}\) make concentric circles whose centre is the wire.

  

  Direction of magnetic field \(\vec{B}\) can be determined using with Ampère's right-hand grip rule. If you place your right-hand thumb in the direction of the current in the wire, bent fingers show the direction of the magnetic field lines.

  The magnitude of the magnetic field B around a long straight conductor carrying current can be determined from the following relation

  \[B= \frac{\mu_o}{2\pi}\,\frac{I}{R},\]

  where I is the current passing through the conductor and R is the perpendicular distance from the conductor whose magnitude of the magnetic field we use in the formula.

  The relationship is given here without derivation because it cannot be deduced by the means of secondary school mathematics. For the detailed derivation using higher mathematics, see the following task: Magnetic Field of a Straight Conductor Carrying a Current.

• Hint Solution: Magnitude and direction of the magnetic force

  When a wire carrying current is located in a magnetic field, it is being influenced by a magnetic force \(\vec{F}_m\), whose magnitude is

  \[F_m=BIl\,\sin{\alpha},\]

  where B is the magnitude of the magnetic field in which the wire is located, and angle α is the angle between the vector of the magnetic field and the direction of the current in the wire.

  Each of the wires lies in the magnetic field created by the other wire. If the wires are parallel to each other, then the vector of this magnetic field is perpendicular to the direction of the current carried by the respective conductor (see figure), therefore

  \[\alpha=90^\circ\,\,\,\Rightarrow\,\,\sin{\alpha} =1.\]

   

  

  We obtain the relation for the magnitude of the magnetic force on the wire carrying current

  \[F_m=BIl,\]

  in which we substitute for the magnetic field B that is created, for example, by the first wire in the location of the second wire, and we substitute I for the current carried by the second wire, or vice versa.

  Directions of the forces can be determined by the Fleming's left-hand rule.

  Fleming's left-hand rule

  If we place our left hand near the wire so that the fingers are showing the direction of the current and magnetic field lines (or vector \(\vec{B}\)) are entering the palm perpendicularly, then the thumb is oriented in the same direction as the vector of the magnetic force \(\vec{F}_m\), which is acting on the wire.

  

• Analysis

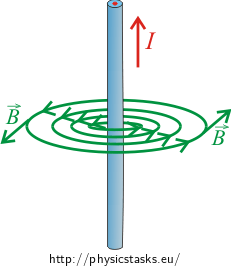
  Each wire carrying electric current creates a magnetic field around itself. We can draw this field after determining the direction of the magnetic field lines using the Ampère's right-hand grip rule.

  Each wire also lies in the magnetic field of the other wire. Since the wires carry electric current and are located in a magnetic field, they are under the influence of a magnetic force. Magnitude of the magnetic force depends on the magnitude of the magnetic field, current carried by the wire, length of the wire and on the wire's position in relation to the vector of the magnetic field. Since the wires are parallel to each other, the direction of the magnetic field is going to be perpendicular to the direction of current in the wire (see more detailed explanation in the Hint section).

  Magnetic field in which one of the wires is located is created by the other wire. We substitute for the magnitude of the field of a long straight wire (in this case, of the second wire) into the relation for the magnitude of the magnetic field. The distance at which we want to determine the magnitude of the magnetic field is equal to the distance between the wires.

  We can apply a similar logic to the other wire, which is located in the magnetic field of the first one. It is also influenced by the magnetic force of the first wire.

  Directions of the forces with which the wires are acting on each other can be determined by the Fleming's left-hand rule.

• Solution of a): Congruent direction of the current

  Each wire carrying electric current creates a magnetic field around itself. We can determine the direction of the magnetic field by the Ampère's right-hand grip rule.

  

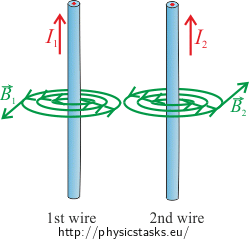
  One wire lies in the magnetic field of the other wire, thus there is a magnetic force acting on the first wire, for which the following holds true:

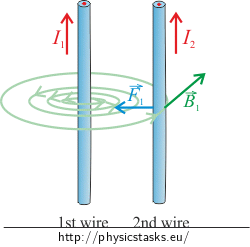
  \[F_2=B_2I_1l\tag{1}\]

  where B₂ is the magnitude of the magnetic field created by the second wire in the place in which the first wire is located, I₁ is the magnitude of the current carried by the first wire.

  For the magnitude of the magnetic field B₂ we have

  \[B_2= \frac{\mu_o}{2\pi}\,\frac{I_2}{R}\]

  where R is the distance from the place in which we are determining the magnitude of the magnetic field. In our case, it is the place where the second wire is. Thus, R is the distance between the wires.

  We substitute the magnitude of the magnetic field B₂ in the formula for the magnitude of the magnetic force F₂ and adjust the formula:

  \[F_2=\frac{\mu_o}{2\pi}\,\frac{I_1I_2}{R}l. \]

  We have obtained the relation for the magnitude of the magnetic force F₂ by which the second wire affects the first one.

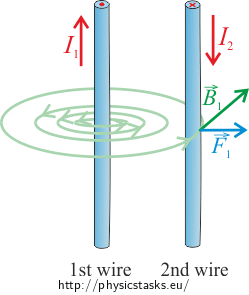
  Direction of the magnetic force can be determined by the Fleming’s left-hand rule. In our case, magnetic force \(\vec{F}_2\) is directed to the right.

  

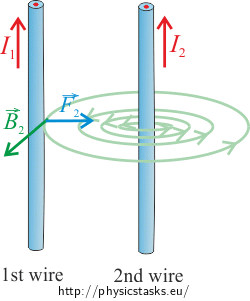
  Note: For the sake of clarity, the picture shows only the magnetic field created by the second wire, as the magnetic force of the second wire \(\vec{F}_2\) influences the first wire exactly because of it.

   

  Likewise, the second wire is located in the magnetic field of the first wire, therefore, it is also influenced by a magnetic force. For the magnitude of this force it holds true:

  \[F_1=B_1I_2l,\]

  where B₁ is the magnitude of the magnetic field of the first wire and I₂ is the magnitude of the current carried by the second wire.

  For the magnitude of the magnetic field B₁ we have:

  \[B_1= \frac{\mu_o}{2\pi}\,\frac{I_1}{R}.\]

  Then we substitute for this expression into the formula for the magnitude of the magnetic force F₁

  \[F_1=\frac{\mu_o}{2\pi}\,\frac{I_1I_2}{R}l.\]

  Direction of the magnetic force \(\vec{F}_1\) can also be determined by the Fleming's left-hand rule. In our case, the force with which the first wire influences the second one is directed to the left.

  

   

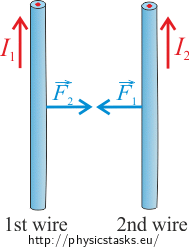
  Magnitudes of the forces \(\vec{F}_1\) and \(\vec{F}_2\) with which the wires are acting on each other are equal. Let's denote this common value as F.

  \[F_1=F_2=F=\frac{\mu_o}{2\pi}\,\frac{I_1I_2}{R}l.\]

  So, wires carrying current are acting on each other by the forces of the same magnitude, but the opposite direction. If we remember the formulation of the Newton's third law (the action-reaction law), then we could come to this conclusion directly from the third law without determining the direction and magnitude of the second force.

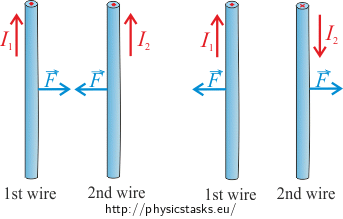
  If the direction of the current carried by the wires is congruent, then the wires are attracted to each other.

  

• Solution of b): Opposite direction of the current

  Around each wire carrying electric current, a magnetic field will arise, and the direction of this field can be determined by the Ampère's right-hand grip rule.

  

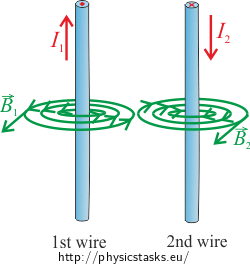
  If we change the direction of the current in the wire, only the direction of the magnetic field and the direction of the force will change. Yet the magnitude of the magnetic force acting on the wires will be the same as in case of the congruent direction of the current. For the magnitude of the magnetic force acting on each wire the relation derived in Solution of a) can be applied:

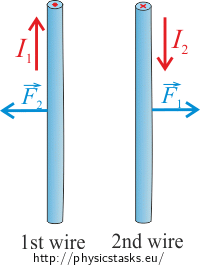
  \[F=\frac{\mu_o}{2\pi}\,\frac{I_1I_2}{R}l.\]

  Direction of the magnetic force acting on the first wire can be determined by the Fleming's left-hand rule. In our case, the magnetic force with which the second wire influences the first one is directed to the left.

  

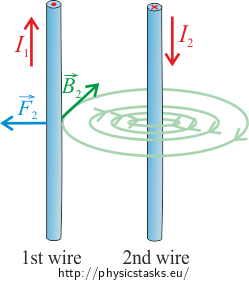
  Direction of the magnetic force acting on the second wire can also be determined by the Fleming's left-hand rule. In our case, the magnetic force with which the first wire influences the second one is directed to the right.

  

  So, wires carrying current are acting on each other by the forces of the same magnitude with the opposite direction, which corresponds with the Newton's third law (the action-reaction law).

  If wires carry current in the opposite direction, the wires will repel each other.

  

• Summary

  If parallel wires are carrying electric current, magnitudes of the forces with which they are acting on each other are equal and the following relation can be applied:

  \[F=\frac{\mu_o}{2\pi}\,\frac{I_1I_2}{R}l.\]

  Direction of the current in the wire affects only the direction of the magnetic force. If the direction of the current in wires is congruent, they attract each other, and in case of the opposite direction of the current, wires repel each other.

  

• Notation and Numerical Substitution

  \(I_1\,=10\,\mathrm{A}\)	current carried by the first wire
  \(I_2\,=20\,\mathrm{A}\)	current carried by the second wire
  \(R\,=\,10\,\mathrm{cm}=0.10\,\mathrm{m}\)	distance between the wires
  \(l\,=\,1\,\mathrm{m}\)	length of the wire
  \(F\,=\,?\)	force acting on a wire of length l
  From the Tables:
  \(\mu_o=4\pi \cdot 10^{-7}\,\mathrm{Hm^{-1}}\)	permeability of vacuum

  ---

  \[F=\frac{\mu_o}{2\pi}\,\frac{I_1I_2}{R}\,l=\frac{4\cdot\pi \cdot 10^{-7}}{2\cdot\pi}\cdot\,\frac{10{\cdot} 20}{0.1}\cdot1\,\mathrm{N}=4{\cdot} 10^{-4}\,\mathrm{N}=0.4\,\mathrm{mN}\]

• Answer

  The magnitude of the forces with which the wires interact with each other does not depend on the direction of the current in the wires and is, in both cases, equal to 0.4 mN.

  If the direction of the current in the wires is congruent, they attract each other, and in case of the opposite directions of the currents, wires repel each other.

• Comment: Definition of the Ampere

  Based on the obtained relation for the magnitude of the magnetic force with which wires interact with each other, the unit of current, ampere, is defined. It is one of the seven base units of the SI.

  Definition of the Ampere

  One ampere is a constant current which, when passing through two straight parallel infinitely long wires of a negligible cross section located in vacuum at a distance of 1 m from each other, causes a force between the wires of the magnitude of 2·10^-7 N on 1 m of the length of the wire.