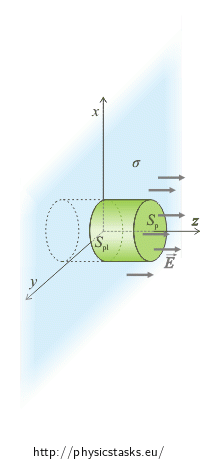
Field of Evenly Charged Plane
Task number: 3249
An evenly spread charge with areal density of σ is located on an infinite plane.
1) Determine the electric field intensity in distance z from the plane.
2) Find the electric potential in distance z from the plane.
Hint: Electric Field Intensity
Since using the Gauss area is handy in this task, we need to think through what area to choose as the Gauss area.
A useful Gauss area would be the surface of a cylinder whose axis is perpendicular to the plane and the plane divides the cylinder in half. Think about the direction of the intensity vector in relation to the base and the sides of the cylinder.
The total flux flowing through the Gauss area can be obtained by adding up the flux flowing through the base and the flux flowing through the sides of the cylinder.
Hint: Electric Potential
Potential is potential energy given for a unit charge
\[\varphi\,=\, \frac{E_p}{Q}\]and potential energy is equal to negative work done by electric forces moving a charge from place with zero potential energy (denoted as A for example) to the given point (denoted as B).
\[E_p(z)\,=\, - \int_A^B \vec{F} \cdot \mathrm{d}\vec{z}\]We divide both sides by charge Q and receive:
\[\varphi\,=\, - \int_A^B \frac{\vec{F}} {Q}\cdot \mathrm{d}\vec{z}\]If we divide force \(\vec{F}\) by charge Q, we obtain electric field intensity \(\vec{E}\).
\[\varphi\,=\, - \int_A^B \vec{E}\cdot \mathrm{d}\vec{z}\]Analysis
The easiest way to find the intensity of the electric field is by using the Gauss theorem given the symmetry of electric charge. The Gauss theorem expresses the relation between the flux of electric intensity flowing through a closed area and the total charge inside this closed area.
The vectors of electric intensity are perpendicular to the plane at all points and their magnitude depends on the distance from the plane only. (The direction of the vector depends on the sign of the charge of the plane.) The reason for this is the symmetry of the charge distribution. Because of this it is sufficient to solve this task for positive values of z only. The vector will only change direction for negative values of z.
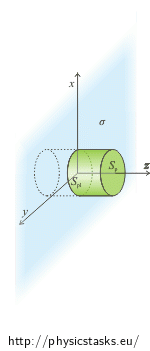
We choose the Gauss area as the surface of the cylinder whose axis is perpendicular to the plane and the plane divides the cylinder in half. The vector of electric intensity is perpendicular to the bases of the cylinder and parallel to the sides of the cylinder in our case. This makes the calculation of the electric intensity flux through the surface of the cylinder easier.
The total intensity flux flowing through the Gauss area can be obtained by adding up the flux flowing through the bases and the flux flowing through the sides of the cylinder.
Potential can be calculated from the electric intensity. Potential at a given point is equal to negative integral of intensity from point with zero potential to the given point.
Solution: Intensity
We will express the electric field intensity using the Gauss theorem.
\[\oint_S \vec{E} \cdot \mathrm{d}\vec{S}\,=\, \frac{Q}{\varepsilon_0}\] \[\oint_S \vec{E} \cdot \vec{n}\mathrm{d}S\,=\, \frac{Q}{\varepsilon_0}\]The electric field around the plane is symmetric since the charge of the plane is spread symmetrical. The vector of electric intensity is perpendicular to the plane at all points and its magnitude depends on distance from the plane z only.
Note: The charged plane in the picture is identical with the xy-plane and it is blue.
We will choose the surface of a cylinder as the Gauss area. We do so because the intensity vector is perpendicular to the bases of the cylinder and parallel with the sides of the cylinder (see picture). This makes the calculation of the scalar product much easier. (A general procedure of How to choose the Gauss area is described in task Field Of Evenly Charged Sphere.)
The total intensity flux flowing through the surface of the cylinder can be obtained by adding up the flux flowing through the sides of the cylinder and the flux flowing through the bases of the cylinder. Since both bases are in the same distance from the plane, intensity has the same value in them. The intensity flux flowing through the bases is the same in both of them and so we will take the flux into account twice. We adjust the lefthand side of the Gauss theorem:
\[\oint_{Spl} \vec{E} \cdot \vec{n}\mathrm{d}S\,+2\oint_{Sp} \vec{E} \cdot \vec{n}\mathrm{d}S\,=\, \frac{Q}{\varepsilon_0}\tag{*}\]Flux through sides:
The intensity vector is parallel with the sides of the cylinder and thus it is perpendicular to the normal vector. The scalar product of both vectors is zero and so the intensity flux flowing through the sides is zero.
\[\oint_{Spl} \vec{E} \cdot \vec{n}\mathrm{d}S\,=\, 0\]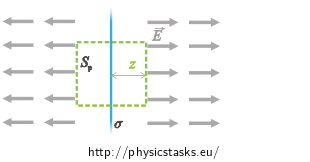
Flux through base:
The intensity vector is perpendicular to the base at all points and thus it is parallel with the normal vector. This allows us to simplify the scalar product:
\[ \vec{E} \cdot \vec{n} \,=\, En\,=\,E\](note: \(\vec{n}\) is unit vector).
Using these pieces of information, we can adjust the integral at the left hand side of the Gauss theorem and express the flux flowing through the base of the cylinder.
\[\oint_{Sp} \vec{E} \cdot \vec{n}\mathrm{d}S\,=\,\oint_{Sp} E n\mathrm{d}S\,=\, \oint_{Sp} E\mathrm{d}S\]The magnitude of intensity vector E is the same at all point of the base and so we can factor it out of the integral as a constant. We receive the following relation:
\[\oint_{Sp} \vec{E} \cdot \vec{n}\mathrm{d}S\,=\,E \oint_{Sp} \mathrm{d}S\,=\,E S_p\]where Sp is the area of the Gauss cylinder base.
We substitute the result back into the Gauss theorem (*). We must not forget that the cylinder has two bases and so we have to count the flux flowing through the base twice.
\[2 E S_p\,=\, \frac{Q}{\varepsilon_0}\]Now we need to express charge Q inside the Gauss area. The plane inside the Gauss cylinder has area of Sp. We can express the charge using the area of this part of the plane and the area charge density: Q = σSp.
\[2 E S_p\,=\, \frac{\sigma S_p}{\varepsilon_0}\]We express the magnitude of charged plane electric field intensity:
\[E \,=\, \frac{\sigma}{2 \varepsilon_0}\]We have calculated that the magnitude of intensity is not dependent on the distance from the plane. Infinite charged plane creates a homogenous field around itself.
Solution: Potential
Potential at point A is equal to the negative intensity integral from point with zero potential to point A which is in distance z from the plane. (More detailed explanation can be found in hint.) We often chose the zero potential to be in infinity, let us try it in this task as well.
\[\varphi (z)\,=\, - \int_{\infty}^z \vec{E} \cdot \mathrm{d}\vec{z}\]Potential is independent of the integration path so our choice is arbitrary. We will choose a line that is perpendicular to the plane in this task.
Electric intensity vector \(\vec{E}\) is parallel with vector \(\vec{z}\) and so we can simplify the integral:
\[\varphi (z)\,=\, - \int^{z}_{\infty} E \mathrm{d}z \]Since the magnitude of electric intensity is constant, we can factor it out from the integral:
\[\varphi (z)\,=\, - E \int^{z}_{\infty} \mathrm{d}z \]We calculate the definite integral:
\[\varphi (z)\,=\, - E \,[z]^z_\infty \]We can see from the result that the choice of zero potential in infinity is not a handy one because the integral cannot be „finished“. Let us try to have the zero potential right in the charged plane were z = 0. The only difference will be in the lower limit of the integral.
\[\varphi (z)\,=\, - E \int^{z}_{0} \mathrm{d}z \,=\, - E \,[z]^z_0 \,=\, - E z \]Now we can finish the integral calculation and so the choice of zero potential was convenient. (Note: Similar „problems“ with zero potential point choise apply for all charged bodiess with charge in infinity.)
We substitute the magnitude of electric intensity which was calculated in the previous section.
\[\varphi (z) \,=\,- \,\frac{\sigma }{2 \varepsilon_0}\,z\]The potential is the greatest at the charged plane and then it declines linearly.
Since we solved the task on one side only (for z > 0), it is necessary to note that the other side is analogous and the potential declines linearly as well. If we understand z to be the distance from the plane then the obtained relation applies for all points in space. If z is to be a coordinate then we need to add the absolute value of it into the obtained relation.
\[\varphi (z) \,=\,- \,\frac{\sigma }{2 \varepsilon_0}\,|z|\]Answer
Infinite charged plane creates a homogenous field around itself with intensity of
\[E (z) \,=\,\frac{\sigma }{2 \varepsilon_0}\,.\]The vectors of electric intensity are perpendicular at all points to the plane and point away from the plane in case of positive charge and towards the plane in case of negative charge.
Electric field potential of the plane is the biggest at the charged plane and then linearly declines with distance (given the plane is charged positively).
\[\varphi (z) \,=\,- \,\frac{\sigma }{2 \varepsilon_0}\,|z|\]Note: z is considered to be the distance from the plane, not a coordinate.
Graphs
We will consider the plane to be charged with positive charge while plotting graphs.
Electric intensity dependence on distance from plane graph
The magnitude of electric intensity is constant: \(E\,=\,\frac{\sigma}{2 \varepsilon_0}\)
The graph is a positive constant function for positive values of z and negative for negative values of z. The reason for this is the electric intensity vector having the opposite direction on the other side of the plane.
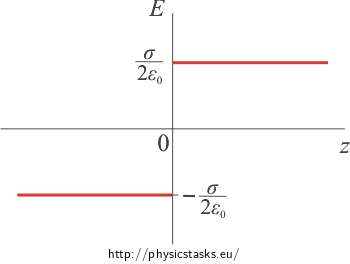
Note: The electric field intensity is generally continuous with exception for points located at the plane itself. The tangent components of the vectors remain continuous but the normal components change „with a jump“ which is proportional to the areal charge density. This is true for our case as well.
Electric potential dependence on distance from plane graph
The potential is the greatest at the charged plane (for z = 0).
It then declines with distance from the plane linearly.
\[\varphi (z)\,=\,- \,\frac{\sigma}{2 \varepsilon_0}\,|z|\]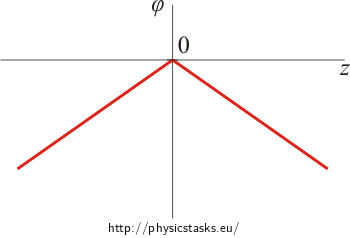
Note: The electric potential is always continuous because it is linked to the work done while moving a unit charge. The work done cannot change „with a jump“. The potential has its first derivatives continuous as well.