Eight charges in vertexes of an octagon
Task number: 547
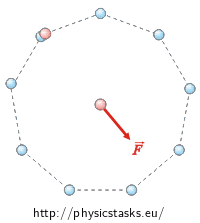
Eight equal charges Q are placed in vertexes of a regular octagon.
a) Which force affects the charge q in the middle of this octagon?
b) Suppose that we remove one of the eight charges Q. Which force will affect the charge q in this case?
c) Now we will place nine equal charges Q in vertexes of a regular nonagon. Which force affects the charge q in the middle of this nonagon? Then we will remove one charge Q from a vertex. Which force will affect the charge q in the middle now?
Note: Parts a) and b) are solved in two different ways.
Note: Signs of charges
We choose that charges Q are negative (blue in pictures) and charge q is positive (red in pictures). The reason for this is a good arrangement of the pictures. Think about the changes of the signs of the charges - if we choose the signs in a different way, the process of the solution will be the same, only the directions of forces can change.
a) Hint
Draw a picture of the forces which affect charge q.
The first way of the solution:Use the fact, that there is an even number of charges Q. What is the resultant force from charges Q placed in the opposite vertexes?
The second way of the solution:Try to add the vectors of forces graphically.
a) Solution using symmetry
Force which each charge Q with affects and the charge q depends on both charges and the distance between them. Since all charges Q are equal and are placed in the same distance from the charge q, all forces affecting the charge q have the same magnitude. Only the directions are different (see the picture).
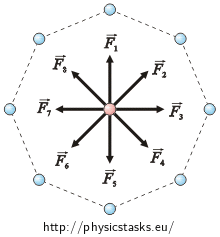
We can see in the picture that charges, which are in opposite vertexes, affect the charge q in the opposite directions. Since these forces have the same magnitude, the resultant force is zero. Realizing this we can do the same with all the opposite pairs of charges. So, the resultantforce which affects the charge q is zero.
a) More general solution
All charges in vertexes of an octagon are equal and they are in the same distance from the charge q. So, forces, which affect the charge in the middle of the octagon, have the same magnitude. We can draw these forces in the picture.

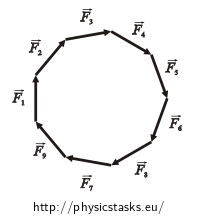
Now we will add all vectors graphically. One possibility is to place each vector one after the other so that the beginning of each vector is connected to the tip of the previous vector. We will gain the resultant force when we connect the start of the first vector with the tip of the last vector.
So we will place all vectors one after the other. We will start for example with the vector marked in the picture as \(\vec{F}_1\) and then add other vectors clockwise.
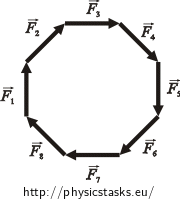
We can see in the picture that all the vectors create a regular octagon. When we place the last vector, we will be at the starting point again. So, the resultant force which affects the charge q is zero.
b) Hint
The first way of the solution:Draw a picture again. Solve it similarly as in the solution of part a).
What is the resultant force if there is an empty space in the opposite vertex of one of the charges?
The second way of the solution:Use the previous result for the solution: Force which eight charges affect the charge in the middle with is zero.
Try to sort out, which charge we must add and where to place it so that the resulting situation will be the same as if we removed one charge.
b) Solution using symmetry
We will solve it similarly as in the solution of part a). The charges which are in opposite vertexes affect the charge q with an equal magnitude of forces and opposite directions. So, the resultant force of both forces is zero. Following this idea we can do the same with all the other charges except for the one which has no chargein the opposite vertex (see the figure on the left).
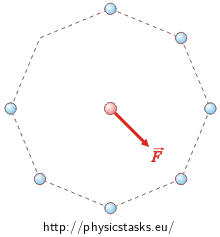
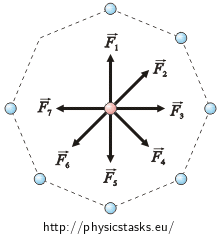
So the resultant force affecting the charge q is equal to the force which is caused by charge Q, which has an empty space in the opposite vertex (see the figure on the right). We can calculate its magnitude from Coulomb´s law:
\[F\,=\, \frac{1}{4 \pi \varepsilon_0} \frac{Qq}{r^2}\,,\]where r is the distance between charges.
b) Solution using a trick
If we want to use the result from the previous part for the solution we can use a small trick and make small changes in the assignment of the task. We know that if there is one charge Q in each vertex of the octagon, then the resultant force affecting the charge q is zero. Now we should remove one charge Q. But the situation will be the same as we add the same charge with an opposite sign to one of the vertexes. In the left picture you can see that vectors \(\vec{F}_8\) and \(\vec{F}_9\) subtract themselves.
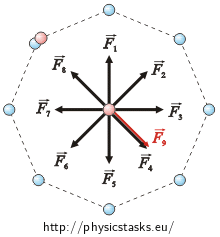

There are two charges now in one of the eight vertexes and they have equal magnitude but opposite signs. The effects of both of these charges will cancel each other out. So the situation is the same as if there were no charge in the vertex.
Now we can calculate the resultant force which affects the charge q.
The resultant force from the eight equal charges is zero (see part a). So, the resultant force which affects the charge q is the same as the force which the positive charge Q affects it with. We can calculate the magnitude of this force from Coulomb’s law:
\[F_e\,=\, \frac{1}{4 \pi \varepsilon_0} \frac{Qq}{r^2}\,,\]where r is the distance between the charges.
c) Hint
Solve this task similarly as you did with the octagon. But this time we can’t use symmetry. We must use adding of the vectors and a small trick with adding the opposite charge.
c) Solution
The solution will be the same as in the previous part. One difference is that in this case we can’t use symmetry. So we can solve this task only in one way.
All charges Q have an equal magnitude and distance from the charge q. So, the forces which these charges affect the charge in the middle of the nonagon with have equal magnitude. We gain the resultant force by adding the vectors of these forces. If we place the vectors after one another, they will form a regular nonagon. So, the resultant force is zero.
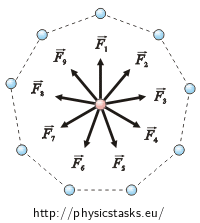
Instead of removing of one charge, we can add one equal charge with the opposite sign to one of the vertexes. Affecting forces of the nine equal charges cancel each other out. So, the resultant force is equal to the force which the positive charge Q affects the charge in the middle of the nonagon with.
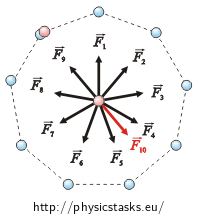
We can calculate its magnitude from Coulomb’s law:
\[F\,=\, \frac{1}{4 \pi \varepsilon_0} \frac{Qq}{r^2}\,.\]Answer
The resultant force, which affects the charge q in the middle of the octagon or nonagon is zero.
If we remove one charge from the vertex of the octagon or nonagon, then the magnitude of the resultant force affecting the charge q will be:
\[F\,=\, \frac{1}{4 \pi \varepsilon_0} \frac{Qq}{r^2}\,.\]How would this work for a regular polygon
Notice that the process of the solution for the nonagon and octagon was the same. If we have any regular n-gon the process will be the same again.
If there is one charge in each vertex then the resultant force is zero. If we remove one charge the resultant force will be equal the force from the opposite charge placed in one of the vertexes.
If there is an even number of the vertexes of the polygon, we can use symmetry and solve the task equally as we have solved it in the case of the octagon.




