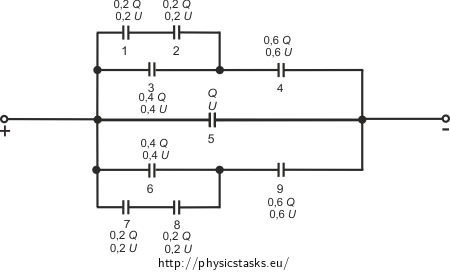
Connecting Capacitors II
Task number: 2322
Capacitors with identical capacity of C are connected according to the picture. Determine the total capacity as well as voltage and charge on every capacitor given that the total voltage is U.
Hint
If you are unsure how to work with circuits with capacitors, go through task Connecting Capacitors 1.
The key to success is redrawing the circuit into a more „common form“ so that the connections remain the same and it is more obvious which capacitors are in parallel and which are in series.
Solution – capacity
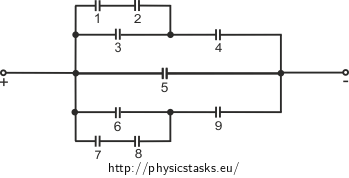
We will redraw the diagram of capacitors into a more common form and we will number the capacitors for clarity.
We will conduct the calculation of this task analogically to task Connecting Capacitors 1. If this task is too difficult for you, go through task Connecting Capacitors 1 first. The procedure is explained in more detail there.
Now we will connect the capacitors one by one using relations for connecting capacitors in parallel and in series capacitors (see Connecting Capacitors 1, Hint Solution – Capacitance a Connecting Capacitors 1, Hint Solution – Voltage and Charge). We will also utilize the symmetry of the circuit so that we do not have to make some calculations twice (all capacitors have the same capacity C).
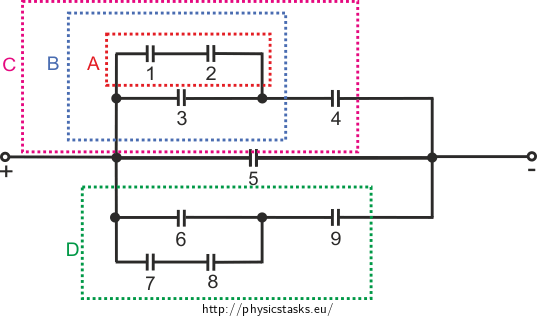
Capacitors 1 and 2 are in series:
\[\frac {1} {C_{1{,}2}} = \frac {1} {C} + \frac {1} {C},\] \[C_\mathrm{A}={C_{1{,}2}} = \frac {C} {2}.\]Capacitors A and 3 are in parallel:
\[C_\mathrm{A,3} = C_\mathrm{A} + C,\] \[C_\mathrm{B}=C_\mathrm{A,3} = \frac {3}{2}C.\]Capacitors B and 4 are in series:
\[\frac {1}{C_\mathrm{B,4}}= \frac {1}{C_\mathrm{B}} + \frac {1} {C_4} = \frac {2} {3C} +\frac {1}{C},\] \[C_\mathrm{C} = C_\mathrm{B,4} = \frac {3} {5} C.\]We can write the following due to symmetry:
\[C_\mathrm{D} = C_\mathrm{C}= \frac {3} {5} C.\]Now we can redraw the circuit once more.
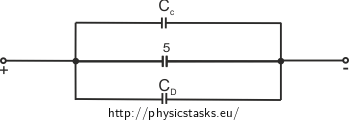
Capacitors \(C_\mathrm{C}, C_\mathrm{D}\) and 5 are in parallel:
\[C_\mathrm{C, D, 5} = C_\mathrm{C} + C_\mathrm{D} + C_5=\frac{3}{5}C + \frac{3}{5}C +C ,\] \[C_\mathrm{V} = C_\mathrm{C, D, 5} = \frac {11}{5}C.\]The total capacity of the circuit is \(C_\mathrm{V} = \frac {11} {5} C.\)
Hint – Relations For Charge And Voltage On Capacitors
The following relation applies between the capacity, the voltage and the charge of a capacitor:
\[Q = UC.\]The charge of capacitors in series is the same. The voltage splits:
\[Q = Q_1 = Q_2,\] \[U = U_1 + U_2.\]The charge of parallel capacitors splits. The voltage is the same:
\[Q = Q_1 + Q_2,\] \[U = U_1 = U_2.\]We will go the opposite way when calculating the voltage and charge than when calculating the capacity. We will start with the circuit where all capacitors are replaced by a single one and we will gradually return to the „original“ circuit.
Solution – Voltage And Charge

Let us now return to the circuit with capacitors C, D and 5. The voltage on all these capacitors is equal (see hint) and is the same as voltage U on the whole circuit:
\[U_\mathrm{C} = U_\mathrm{D} = U_5 = U.\]We will use the following general equation to calculate charge:
\[Q = U C.\tag{1}\]We will therefore receive:
\[Q_\mathrm{C}=C_C U=\frac {3} {5} C U,\] \[Q_\mathrm{D}=C_D U=\frac {3} {5} C U,\] \[Q_5= C U.\]
Capacitor C was created by substituting for capacitors 4 and B connected in series. Charges on capacitors in series are equal:
\[Q_4 = Q_B = Q_C=\frac {3} {5} C U. \]We will calculate the voltage from relation (1):
\[U_4 = \frac {Q_4}{C_4} = \frac {3}{5}U,\] \[U_\mathrm{B} = \frac {Q_4}{C_B} = \frac {2}{5}U.\]Capacitor B was created by substituting for capacitors 3 and A connected in parallel. The voltage on parallel capacitors is equal:
\[U_3 = U_\mathrm{A} = U_\mathrm{B} = \frac {2} {5}U.\]We will calculate the charges from equation (1):
\[Q_3 = C_3 U_3 = \frac {2} {5}CU,\] \[Q_\mathrm{A} = C_\mathrm{A} U_\mathrm{A} = \frac {1} {5}CU.\]Capacitor A was created by substituting for capacitors 1 and 2 connected in series. Charges on capacitors in series are equal:
\[Q_1 = Q_2 = Q_\mathrm{A} = \frac {1} {5} CU.\]We will calculate the voltage from relation (1):
\[U_1 = \frac {Q_1}{C_1} = \frac {1} {5} U,\] \[U_2 = \frac {Q_2}{C_2} = \frac {1} {5} U.\]We do not have to calculate the voltage and charge on capacitors 6, 7, 8, and 9 since the circuit is symmetrical (and the capacitors have equal capacity). Their values will be equal to the values of capacitors that are located symmetrically across the axis of symmetry. For example, capacitor 1 will have the same charge and voltage as capacitor 7.
Answer
The total capacity of the circuit is \(C_\mathrm{V} = \frac {11} {5}C.\)
The charges and voltages on capacitors are:
\[Q_1 = Q_7= \frac {1} {5}CU \quad Q_2=Q_8 = \frac {1} {5}CU \qquad Q_3=Q_6 =\frac{2}{5}CU \qquad Q_4=Q_9 =\frac {3} {5} CU \qquad Q_5 = CU \] \[U_1=U_7= \frac {1} {5}U \qquad U_2=U_8 = \frac {1} {5}U \qquad U_3=U_6 = \frac {2}{5}U \qquad U_4=U_9 = \frac {3} {5} U \qquad U_5 = U. \]In the following diagram, \(Q=UC\) denotation was used where U is the voltage of the source and C is the capacity of each of the capacitors.