Collection of Solved Problems in Physics

Charged Line Segment 1

Task number: 2319

• Hint: Denotation of Values and Picture

  We denote the length of the line segment by l and the distance of point A from the end of the line segment by d.

  Now we chose the coordinate system and we draw a picture. We set the origin to point A.

  

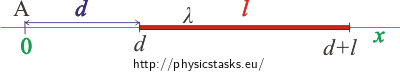
• Hint: Connection to Point Charge

  Positive point charge Q causes electric field of intensity of

  \[E\,=\, \frac{1}{4 \pi \varepsilon_0}\, \frac{Q}{r^2}\,\]

  at distance r. The vector of intensity points away from the charge.

  Think through how we can use this knowledge in this task.

• Hint Solution

  We will separate the line segment into smaller pieces that will behave like point charges.

  We will then obtain the total intensity by „adding up“ (more precisely by integrating) all contributions of these small bits.

• Analysis

  First, we chose the coordinate system. The whole line segment will lie on the x-axis and point A will be placed to the origin. In this case, the vector of intensity will also lie on thex-axis.

  We will separate the charged line segment into smaller parts that will behave like positive point charges. The total intensity can thus be obtained by integrating all contributions of intensity of these smaller parts of the line segment.

  The vector of intensity has the same direction for all contributions of intensity: the direction of the x-axis. The total intensity will thus have this direction as well.

• Solution

  First we choose the coordinate system.

  We will set the origin to point A. The charged line segment will lie on the x-axis in distance of d from point A (from the origin). The ends of the line segment will thus have coordinates d and d + l.

  

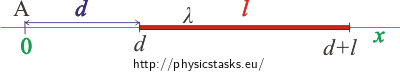
  We know that positive point charge Q causes electric field of intensity:

  \[E\,=\,\frac{1}{4 \pi \varepsilon_0}\, \frac{Q}{r^2}\,\]

  at distance r. The vector of intensity points away from the charge.

  We will separate the line segment into smaller pieces of length of dx that will be charged with charge of dQ = λdx where λ is the length charge density. These pieces will behave like point charges.

  

  One such bit will cause electric field of intensity:

  \[\mathrm{d}E\,=\,\frac{1}{4 \pi \varepsilon_0}\, \frac{\mathrm{d}Q}{r^2}\,=\,\frac{1}{4 \pi \varepsilon_0}\, \frac{\lambda \mathrm{d}x}{x^2}\,\tag{*}\]

  in point A (that is in distance x). The vector of intensity has the same direction for all contributions of intensity: the direction of the x-axis, away from the line. The total intensity will thus have the same direction.

  We will obtain the total intensity by integrating all contributions across the whole length of the line segment.

  \[E\,=\int_{d}^{\small d+l} \mathrm{d}E\]

  We will substitute for the contributions from relation (*)

  \[E\,=\int_{d}^{\small d+l} \frac{1}{4 \pi \varepsilon_0}\, \frac{\lambda \mathrm{d}x}{x^2}\,.\]

  We factor out the constants

  \[E\,=\,\frac{\lambda}{4 \pi \varepsilon_0}\int_{d}^{\small d+l} \frac{1}{x^2}\,\mathrm{d}x\]

  and then we calculate the definite integral.

  \[E\,=\,\frac{\lambda}{4 \pi \varepsilon_0}\,\left[ -\frac{1}{x}\right]_{d}^{\small d+l}\,=\,\frac{\lambda}{4 \pi \varepsilon_0}\,\left(-\,\frac{1}{d+l}\,+\, \frac{1}{d}\right) \]

  The expression in the parentheses can be transfered to the same denominator.

  \[E\,=\,\frac{\lambda}{4 \pi \varepsilon_0}\,\frac{-d+d+l}{d \left( d+l\right)} \,=\,\frac{\lambda}{4 \pi \varepsilon_0}\,\frac{l}{d \left( d+l\right)}\]

  Now all the remains is to express charge density λ using total charge Q and length l of the line

  \[\lambda\,=\,\frac{Q}{l}\]

  and substitute into relation

  \[E\,=\,\frac{Q}{4 \pi \varepsilon_0 l}\,\frac{l}{d \left( d+l\right)}\,=\,\frac{Q}{4 \pi \varepsilon_0 }\,\frac{1}{d \left( d+l\right)}\,.\]

  We obtain the value of the intensity of the electric field in distance d from the end of the line segment.

• List of known information and numerical calculation

  Q = 0.2 nC = 2 · 10⁻¹⁰ C

  l = 60 cm = 0.6 m

  d = 10 cm = 0.1 m

  E = ? (V m⁻¹)

  From tables:

  ε₀ = 8.85 · 10⁻¹² C² N⁻¹ m⁻²

  ---

  \[ \begin{eqnarray} E\,& =& \,\frac{Q}{4 \pi \varepsilon_0 }\,\frac{1}{d \left( d+l\right)}\,=\,\frac{2\cdot\,10^{-10}}{4 \pi 8.85{\cdot}10^{-12} }\,\frac{1}{0.1 \left( 0.1\,+\,0.6\right)}\,\mathrm{V\,m^{-1}}\\ E\,& \dot=& \,25.69\,\mathrm{V\,m^{-1}} \end{eqnarray}\]

• Answer

  The intensity of the electric field d = 10 cm away from the end of the charged line segment has the value of:

  \[E\,=\,\frac{Q}{4 \pi \varepsilon_0 }\,\frac{1}{d \left( d+l\right)}\,\dot=\,25.69\,\mathrm{V\,m^{-1}}\,.\]

  The vector of the electric intensity points away from the line segment.

• Link

  The value of intensity outside of the line upon which the line segment lies is calculated in task Charged line segment.