Collection of Solved Problems in Physics

Magnetic Field inside a Solenoid

Task number: 1785

Derive the formula for the amplitude of the magnetic B-field of a solenoid that has n turns per 1 m of its length and is carrying a current I.

• Hint — Solenoid

  A solenoid is a long conductor that is densely wound to form a cylindrical helix. The length of the solenoid is much longer than its diameter, thus we can neglect the imperfections of the field at the ends of the winding.

  A solenoid is characterized by the number of turns N of the conductor and length of the solenoid l. The density of turns per unit length n is then:

  \[n=\frac{N}{l}.\]

• Hint — Magnetic field of a solenoid

  We can estimate the arrangement of the magnetic field of the solenoid from the magnetic field of individual loops of the conductor. The fields of individual conductor loops sum up to the total field of the solenoid.

  

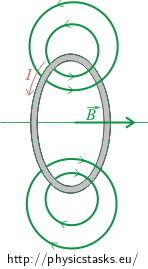
• Hint — Ampére’s law

  Amepère’s law is used to calculate the magnitude of the magnetic \(\vec{B}\)-field in some symmetrical cases, similarly as the Gauss’ law is used to calculate the magnitude of electric \(\vec{E}\)-field in symmetrical cases in electrostatics.

  The mathematical formulation of Ampère’s law is:

  \[\int_l \vec{B}\cdot \,\mathrm{d}\vec{l}=\mu_o I_c,\]

  where I denotes the total electric current passing through Ampère’s curve l.

• Analysis

  We can assess the distribution of the magnetic field of the solenoid from the magnetic field of individual turns of the conductor. In the case of a sufficiently long and densely wound coil (which is the informal definition of the solenoid), the magnetic field of all turns of the conductor sum so that there is a homogeneous total magnetic field inside the solenoid.

  

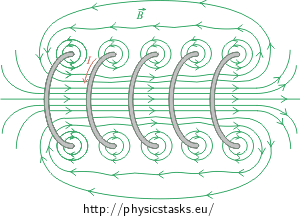
  The vector of the magnetic B-field inside the solenoid directs along the axis of the solenoid. We determine its orientation by using the right-hand rule. The contributions from opposite sides of each individual turn of the conductor outside of the solenoid act against each other and the field is much less intensive than inside the solenoid. It follows that we can the neglect the outer field in the case of a very long solenoid. We determinde the field inside the solenoid using Ampère’s law (see the Hint).

• Solution

  We consider the field outside the solenoid to be approximately zero and the field inside the solenoid to be approximately homogeneous (as derived in the previous section in more detail). We assess the magnitude of the magnetic B-filed by using Ampère’s law:

  \[\int_l \vec{B}\cdot \,\mathrm{d}\vec{l}=\mu_o I_c.\tag{1}\]

  We use a rectangle denoted ABCD as the Ampère’s curve, with two sides of length h parallel to the axis of the solenoid.

  

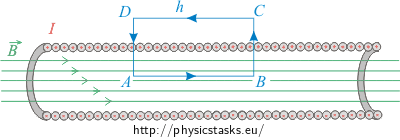
  We can divide the integral on the left-hand side of Ampère’s law (1) into four integrals, each for one side of the rectangle.

  \[\int_{ABCD} \vec{B}\cdot \,\mathrm{d}\vec{l}=\int_{A}^{B} \vec{B}\cdot \,\mathrm{d}\vec{l}+\int_{B}^{C} \vec{B}\cdot \,\mathrm{d}\vec{l}+\int_{C}^{D} \vec{B}\cdot \,\mathrm{d}\vec{l}+\int_{D}^{A} \vec{B}\cdot \,\mathrm{d}\vec{l}.\tag{2}\]

  The first integral on the right-hand side of equation (2) is:

  \[\int_{A}^{B} \vec{B}\cdot \,\mathrm{d}\vec{l}=Bh.\]

  The second and the fourth integrals are equal to zero because the vector of the magnetic \(\vec{B}\)-field is either perpendicular to path section \(\mathrm{d}\vec{l}\) and thus the scalar product along the rectangle sides BC and DA is zero:

  \[\vec{B}\,\cdot\, \mathrm{d}\vec{l}=0.\]

  The third integral along the rectangle side CD is almost zero as the magnetic field is negligible outside the solenoid.

  We thus get for the whole rectangular loop

  \[\int_l \vec{B}\cdot \,\mathrm{d}\vec{l}=Bh.\]

  The total current I_tot enclosed inside the rectangular Ampère’s loop is not only the current I since there are many turns of the conductor inside the rectangle. Denoting n the density of turns per unit length, we get

  \[I_{tot}=nhI\]

  and it follows from Ampère’s law that

  \[Bh=\mu_o nhI.\]

  The magnitude of the magnetic B-field is then

  \[B=\mu_o In.\]

• Comment — Magnitude of magnetic field of a real solenoid

  The magnetic field is weaker and diverges at the ends of a solenoid of finite length. Although we derived the formula of the magnitude of the magnetic B-field

  \[B=\mu_o In\]

  for an infinitely long ideal solenoid, it is valid also for a real solenoid of finite length as long as we are interested in the field sufficiently far from its ends.

  We have derived that the magnitude of the magnetic field inside the solenoid with a given density of turns does not depend on the diameter of the solenoir and is the same everywhere in the cross-section of the solenoid. We can thus use the solenoid to create a homogeneous magnetic field, similarly as we use two parallel capacitor plates to create a homogeneous electric field.

• Answer

  The magnetic B-field inside a solenoid with n turns per unit length carrying a current I is:

  \[B=\mu_o In.\]