Collection of Solved Problems in Physics

“Divided” RLC circuit

Task number: 662

A capacitor with an unknown capacity, a resistor with resistance 50 Omega; and a coil with inductance 0.10 H are connected in series in sn alternating circuit with frequency 50 Hz and amplitude of voltage 300 V. The ratio of amplitudes of the voltage in two parts of the circuit which are marked in the picture is U_m1:U_m2 = 1:2. Calculate the capacity of the capacitor and the amplitude of the current in the circuit.

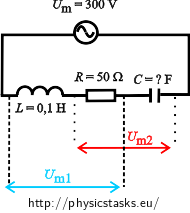
• Notation

  From the assignment we know:

  Frequency of the circuit	f = 50 Hz
  Voltage of the power supply	Um = 300 V
  Resistance of the resistor in the circuit	R = 50 Ω
  Inductance of the coil in the circuit	L = 0.10 H
  Ratio of voltages marked in the picture	Um1:Um2 = 1:2

  We should find out:

  Capacity of the unknown capacitor	C = ? (F)
  Amplitude of a current in the circuit	Im = ? (A)

• Hint 1

  For the RLC circuit connected in series is true that the current which flows through each of the components of the circuit is the same.

• Hint 2

  We can imagine the parts of the circuit with marked voltages as two separate circuits with a given total voltage. Currents which flow through these circuits are the same because it is a RLC circuit in series in fact.

• Analysis

  We have chosen two parts in the circuit in the picture from assigned task. We „know“ the amplitude of the voltage of each of them so we can solve each part as a separate circuit. We use Ohm’s law for an alternating circuit. The current is the same in both of the circuits, so we can formulate the capacity from the ratio of voltages.

  We gain the amplitude of current from Ohm’s law which we use for the whole circuit.

• Expressing of a voltage U_m1 and U_m2

  A coil with an inductance L and a resistor with resistance R are connected to the part of the circuit which belonges to voltage U_m1. The coil and the resistor are connected in series.

  We formulate impedance Z₁ of this part of the circuit:

  \[ Z_1= \sqrt{R^2+(X_L-X_C)^2}=\sqrt{R^2+X_L^2}.\]

  And substitute it to Ohm’s law:

  \[U_{m1}=I_m Z_1=I_m\sqrt{R^2+X_L^2}=I_m \sqrt{R^2+(\omega L)^2}. \]

  Formulas for the second part of the circuit, to which belongs voltage U_m2 are similar. In this circuit we have a resistor with resistivity R and a capacitor with an unknown capacity C:

  \[Z_2= \sqrt{R^2+(X_L-X_C)^2}=\sqrt{R^2+X_C^2}\] \[U_{m2}=I_m Z_2=I_m\sqrt{R^2+X_C^2}=I_m \sqrt{R^2+\frac{1}{(\omega C)^2}}. \]

• Expressing a capacity C and an amplitude of a curren I_m

  From the assignment we know the ratio of both voltages. So we replace it with formulas which we derive from voltages in previous part:

  \[\frac{U_1}{U_2}= \frac{I_m\sqrt{R^2+(\omega L)^2}}{I_m\sqrt{R^2+\frac{1}{(\omega C)^2}}}\]

  The amplitude of current I_m is the same for both formulas so we can reduce it.

  \[\frac{1}{2}= \frac{\sqrt{R^2+(\omega L)^2}}{\sqrt{R^2+\frac{1}{(\omega C)^2}}}\]

  Express unknown capacity C:

  \[\frac{1}{4}=\frac{R^2+(\omega L)^2}{R^2+(\frac{1}{\omega C})^2}\] \[ R^2+(\frac{1}{ \omega C})^2=4(R^2+( \omega L)^2)\] \[(\frac{1}{ \omega C})^2=3R^2+4( \omega L)^2\] \[( \omega C)^2=\frac{1}{3R^2+4( \omega L)^2}\] \[C=\frac{1}{\omega \sqrt{3R^2+4(\omega L)^2}}.\]

  We should express the amplitude of the current from Ohm’s law for the whole circuit. From the assignment we know the amplitude of the voltage of the power supply U_m. There are all three segments in the circuit so we need all three quantities for the formula of impedance – resistance, capacitive reactance and inductive reactance.

  \[I_m=\frac{U_m}{Z}=\frac{U_m}{\sqrt{R^2+(\omega L-\frac{1}{\omega C})^2}}\]

• Numerical solution

  Capacity of the capacitor:

  \[C=\frac{1}{\omega \sqrt{3R^2+4(\omega L)^2}}=\frac{1}{2 \cdot \pi \cdot 50 \sqrt{3{\cdot} 50^2+4(2\cdot \pi\cdot 50{\cdot} 0.1)^2}}\,\mathrm{F}\] \[ C \dot= 30 {\cdot} 10^{-6} \,\mathrm{F}=30\,\mathrm{\mu F}\]

  Amplitude of the current:

  \[I_m=\frac{U_m}{Z}=\frac{U_m}{\sqrt{R^2+(\omega L-\frac{1}{\omega C})^2}}\] \[I_m=\frac{300}{\sqrt{50^2+(2\cdot\pi\cdot 50 {\cdot} 0.1 - \frac{1}{2\cdot \pi \cdot 50 {\cdot} 30\cdot 10^{-6}})^2}}\,\mathrm{A} \] \[I_m \dot= 3.3 \,\mathrm{A} \]

• Answer

  Capacity of the capacitor connected in series is approximately: C = 30 μF.

  Amplitude of the alternating current in the circuit is approximately: I_m = 3.3 A.