Charged Hoop
Task number: 2316
Find
a) electric intensity \(\vec{E}\),
b) potential \(\varphi\)
using direct integration at points located on the axis of a hoop with the radius of R. The hoop is charged with linear density \(\lambda\).
c) Verify the relation between \(\vec{E}\) and \(\varphi\).
Hint a)
Positive point charge Q creates a field of intensity
\[{E}=\frac{1}{4\pi\epsilon_0}\frac{Q}{r^2}\]at the distance of r. The vector of intensity \(\vec{E}\) points in the opposite direction of the charge if Q is positive. In the other case, the vector points towards the charge.
Think of how we could use this knowledge in our task.
Solution of a)
Positive point charge Q creates a field of intensity
\[{E}=\frac{1}{4\pi\epsilon_0}\frac{Q}{r^2}\]at the distance of r.
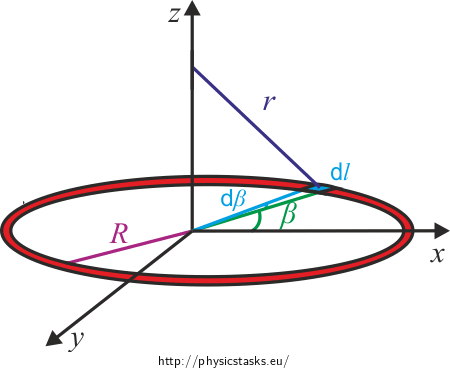
If the hoop is charged with linear density \(\lambda\), then charge dQ on infinitely small part of the hoop dl has the following value
\[\textrm{d}Q = {\lambda} {\textrm{d}l},\]where \(\textrm{d}l=R \textrm{d}\beta\).
Then
\[\textrm{d}Q =\lambda R \textrm{d}\beta\]and thus
\[\textrm{d}{E}=\frac{1}{4\pi\epsilon_0} \frac{\textrm{d}Q}{r^2}=\frac{1}{4\pi\epsilon_0} \frac{\lambda R}{r^2}\textrm{d}\beta.\tag{1}\]Without loss of generality, we can suppose that the hoop is charged positively. Now we will focus on the direction of the intensity. We will utilize the symmetry of the hoop.
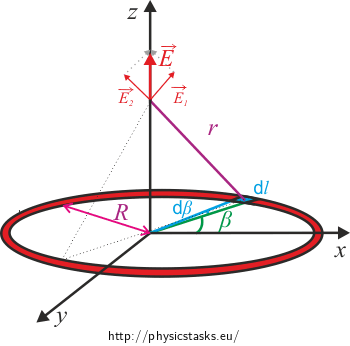
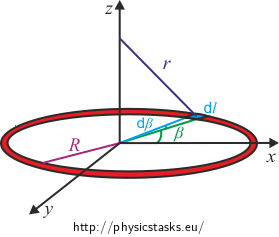
It is clear from the picture that the intensity direction will be the same as the direction of the z-axis since the x–part of the intensity contribution from a small part of the hoop will cancel out with the x–part of the intensity contribution from a small part of the hoop that is symmetrically opposite to the former. The y–part will also be zero.
Note: If we imagined all the intensity contributions from all small bits of the hoop, then they would fill the surface of a cone. It is obvious from this that their sum will point in the direction of the axis of the hoop, i.e. the sum will have only the z–part non-zero.
Now we will turn back to equation (1):
\[\textrm{d}{E}=\frac{1}{4\pi\epsilon_0}\frac{\lambda R}{r^2}\textrm{d}\beta.\]We will draw angle \(\alpha\) and electric intensity pointing in direction z into the picture. In other words, we will express its z component. The other components of electric intensity will not bother us because they will cancel out (see above).
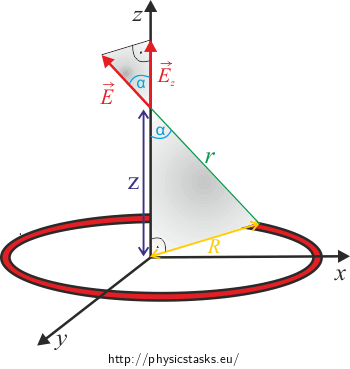
It is clear that
\[\textrm{d}E_\mathrm{z} = \cos \alpha\,\textrm{d}E.\tag{2}\]Note: The value of intensity \(E\) is present in this relation. The value of its component \(E_\mathrm{z}\) too.
Both right angle triangles are similar (they have two identical angles - the right one and \(\alpha\)) so we can write
\[\cos \alpha = \frac {z}{r}\]and we know from Pythagoras theorem
\[r^2 = R^2 + z^2,\]which yields
\[\cos \alpha = \frac{z}{\sqrt{R^2+z^2}}.\tag{3}\]By connecting (1), (2) and (3) we receive
\[dE_\mathrm{z}=\frac{1}{4\pi\epsilon_0} \frac{\lambda R}{z^2 + R^2}\frac{z}{\sqrt{ z^2 + R^2}} d\beta,\] \[dE_\mathrm{z}=\frac{\lambda R}{4\pi\epsilon_0} \frac {z} {\sqrt{(z^2 + R^2)^3}} d\beta,\]which will be integrated across the whole circumference of the hoop, i.e. we will integrate across angle \(\beta\):
\[E_\mathrm{z} = \int_{0}^{2\pi}\frac{\lambda R}{4\pi\epsilon_0} \frac {z} {\sqrt{(z^2 + R^2)^3}} \textrm{d}\beta.\]Distance R and z are independent of angle \(\beta\) and so we can factor them out from the integral:
\[E_\mathrm{z} = \frac{\lambda R}{4\pi\epsilon_0} \frac {z} {\sqrt{(z^2 + R^2)^3}} \int_{0}^{2\pi} \textrm{d}\beta. \]After integration we obtain the following:
\[E_\mathrm{z} = \frac{\lambda R}{4\pi\epsilon_0} \frac {z} {\sqrt{(z^2 + R^2)^3}} {2\pi}, \] \[E_\mathrm{z} =\frac{\lambda R}{2\epsilon_0} \frac {z} {\sqrt{(z^2 + R^2)^3}}. \]Thus \[\vec{E}=\left(0,\ 0,\ \frac{\lambda R}{2\epsilon_0} \frac {z} {\sqrt{(z^2 + R^2)^3}}\right).\]
Hint b)
We will utilize the relation for potential of a point charge just like in part a). The potential of a point charge in the distance of r is
\[\varphi = k\frac{Q}{r}.\]Think of how we could use this relation for the calculation of the potential on the axis of the hoop.
Solution b)
Point charge Q creates potential:
\[\varphi= k \frac {Q} {r}\]in distance r.
If we focus on a single small part of the hoop, the potential of this small part in any given point on the axis of the hoop is
\[\textrm{d}\varphi= k \frac {\textrm{d}Q} {r}\tag{4}\]and since the hoop is charged with linear density \(\lambda\), then this applies:
\[\textrm{d}Q=\lambda\textrm{d}l.\]We will utilize the fact that \(\textrm{d}l=R\textrm{d}\beta\) and thus obtain
\[\textrm{d}Q=\lambda R\textrm{d}\beta.\tag{5}\]From (4) and (5), we subtitute
\[\textrm{d}\varphi=k \frac {\lambda R}{r}\textrm{d}\beta. \tag{6}\]Now we will focus on expressing distance r using the hoop parameters and distance z.
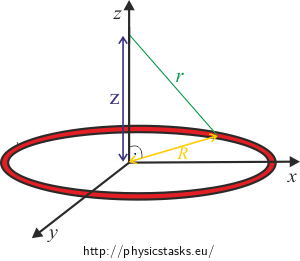
From the right angle triangle in the picture, we can express r using Pythagoras theorem:
\[r=\sqrt{R^2 + z^2}.\tag{7}\]By connecting (6) and (7) we obtain
\[\textrm{d}\varphi=k \frac {\lambda R}{\sqrt{R^2 + z^2}}\textrm{d}\beta.\]Since potential is a scalar, we do not need to worry about its direction and we can integrate all contributions:
\[\varphi=\int_{0}^{2\pi}k \frac {\lambda R}{\sqrt{R^2 + z^2}}\textrm{d}\beta,\] \[\varphi=k \frac {\lambda R}{\sqrt{R^2 + z^2}}\int_{0}^{2\pi}\textrm{d}\beta,\] \[\varphi=k \frac {\lambda R}{\sqrt{R^2 + z^2}}2\pi,\]thus
\[\varphi=\frac {1}{2\epsilon_0} \frac {\lambda R}{\sqrt{R^2 + z^2}}.\]Hint c)
Potential and electric intensity are connected by a relation with the mathematical operator gradient.
Try to recall or find this relation. Remind yourself what the gradient tells us and how to calculate it (in Cartesian coordinates).
Solution c)
We are supposed to prove that the relation mentioned in Hint c) solution
\[\vec{E}=-\thinspace\text{grad}\thinspace\varphi\]holds true.
The prove can be done only for the z component of points located on the axis of the hoop since we determined only the z component of the potential on the axis of the hoop in part b). This should apply for the z component of the electric intensity in points of the axis of the hoop: \(E_\mathrm{z}=-\frac{\partial{\varphi}}{\partial {z}}\). We will calculate the derivative:
\[\frac{\partial{\varphi}}{\partial {z}}=\frac {\lambda R}{2\epsilon_0}(-1)\frac {1}{2} \frac {1}{\sqrt{(R^2 + z^2)^3}} 2z =-\frac {\lambda R}{2\epsilon_0} \frac {z}{\sqrt{(R^2 + z^2)^3}}. \]Thus
\[E_\mathrm{z} = \frac {\lambda R}{2\epsilon_0} \frac {z}{\sqrt{(R^2 + z^2)^3}},\]which is the same relation that we obtained by direct integration in part a).
Now we will prove if the reverse relation hold true as well
\[\varphi=-\int_\infty^{\hat {z}}{E_\mathrm{z}}\textrm{d}z.\]If we substitute the calculated value of \(E_\mathrm{z}\) from part a), we receive
\[\varphi=-\int_\infty^{\hat {z}}{\frac {\lambda R}{2\epsilon_0} \frac {z}{\sqrt{(R^2 + z^2)^3}}}\textrm{d}z.\]We will factor all constants out of the integral:
\[\varphi=-\frac {\lambda R}{2\epsilon_0} \int_\infty^{\hat {z}}{\frac {z}{\sqrt{(R^2 + z^2)^3}}}\textrm{d}z.\]We will have to solve the integral by substitution:
\[a = R^2 + z^2,\] \[\textrm{d}a =2z \textrm {d}z\]and we will recalculate the limits:
\[z \rightarrow \infty \Rightarrow a \rightarrow \infty \qquad;\qquad z = \hat {z} \Rightarrow a = R^2 + \hat {z}^2.\] \[\varphi=-\frac {\lambda R}{2\epsilon_0} \int_\infty^{R^2 + \hat {z}^2} \frac {1}{2a^{3/2}}\textrm{d}a.\]We calculate the integral
\[\varphi=\frac {\lambda R}{2\epsilon_0} \left[\frac {1}{a^{1/2}}\right]_\infty^{R^2 + \hat {z}^2}\]and we substitute the limits
\[\varphi=\frac {\lambda R}{2\epsilon_0} \frac {1}{(R^2 + \hat {z}^2)^{1/2}}.\]Since \(\hat {z}\) is arbitrary point of the z-axis, we can write
\[\varphi=\frac {\lambda R}{2\epsilon_0} \frac {1}{(R^2 + {z}^2)^{1/2}},\]which is the same relation that we received by direct integration in part b).
Graphs of Electric Intensity and Potential
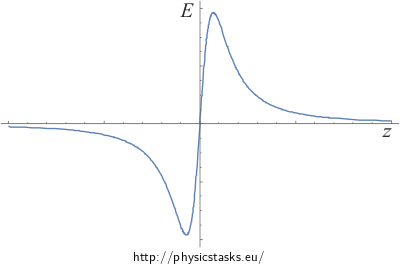
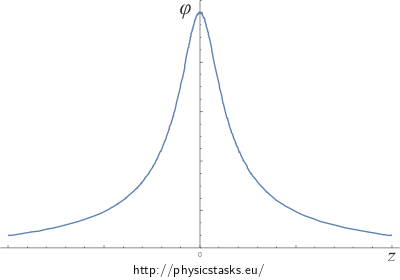
You can see the dependence of electric intensity and potential on distance z from the centre of the hoop.
Answer
The value of electric intensity at the axis of a homogeneously charged hoop is
\[{E}=\frac{\lambda R}{2\epsilon_0} \frac {z} {\sqrt{(z^2 + R^2)^3}},\]intensity points in the direction of the z-axis.
The potential at the axis of a homogeneously charged hoop is \[\varphi=\frac {1}{2\epsilon_0} \frac {\lambda R}{\sqrt{R^2 + z^2}}.\]
We have also proved the relation between \(\vec {E}\) and \(\varphi\).
Similar Task
Task Charged Half-Hoop is similar to this one.