Magnetic Field of a Straight Conductor Carrying a Current
Task number: 1786
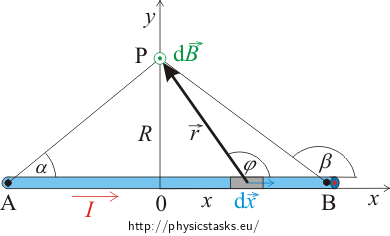
Find the formula for calculating the magnitude of the magnetic B-field at any point P outside of a straight conductor of finite length carrying a constant electric current. Find the formula also for the case of a current-carrying conductor of infinite length.
Hint 1
Draw a picture of the straight conductor with the current and choose and arbitrary point P at a distance of R from the conductor. Segment the conductor into short elements. Every element of the conductor contributes to the magnetic field at point P. The total magnetic field at point P is equal to the sum of the contributions from all elements of the conductor. Making the elements very (infinitely) short, we proceed from summation to integration of the contributions to the magnetic field from inidividual parts of the conductor.
Draw the directions of the contributions to the B-field of several elements of the conductor into the picture and determine the direction of the total magnetic B-field.
Hint 2
We have already said in Hint 1 that we segment the conductor into very short pieces. Each of these pieces contributes to the total magnetic field at poin P. We calculate the total magnetic B-field at point P by integrating over all contributions dB to the field at point P.
Our task is to express all quantities that change when we move along the conductor by using only one variable. The integral is the simplest when we choose the angle formed by the conductor and the connecting line from the conductor element to point P for this variable. Think over, what other quantities that appear in the formula of the magnetic field contribution dB do change when we move along the conductor. Express these quantities using the angle and integrate over the span of the angle.
Analysis
We assess the magnitude of the B-field at any point P outside of the straight conductor carrying the currnet by using the Biot-Savart law.
We consider contributions to the magnetic field at point P from all elements of the straight conductor. The total magnitude of the magnetic B-field at point P is given by an integral over all elements of the conductor
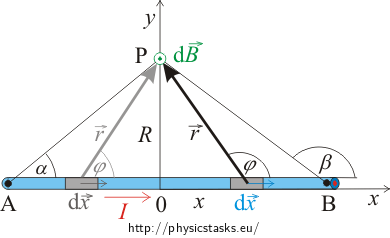
We just shift the endpoints A and B of the conductor to infinity to get the magnitude of the B-field from an infinitely long straight conductor at point P.
Solution 1
We assess the contributions \(\mathrm{d}\vec{B}\) from individual elements of the straight conductor carrying the current using the Biot-Savart law that states:
\[\mathrm{d}\vec{B} = \frac{\mu_o}{4\pi}\, \frac{I\, \mathrm{d}\vec{x}\times \vec{r}}{r^{3}}.\]The absolute value of the vector product is
\[|\mathrm{d}\vec{x}\times\vec{r}|=\mathrm{d}x\,r\,\sin{\varphi},\]where φ is the angle formed by the vectors \(\mathrm{d}\vec{x}\) and \(\vec{r}\).
We have argued in the hint that all the contributions aim in the same direction. We thus get the resulting magnitude of the B-field by integrating over all the contributions dB.
\[B=\int_A^B \mathrm{d}B = \frac{\mu_o}{4\pi}\, \int_A^B\frac{I\, \mathrm{d}x\,r\,\sin{\varphi}}{r^{3}}=\frac{\mu_o}{4\pi}\,I\int_A^B\frac{\sin{\varphi}}{r^{2}}\,\mathrm{d}x.\tag{1}\]Variables r, x and φ change on integrating over the length of the conductor. We express r and x as functions of φ. The distance r is
\[r=\frac{R}{\sin{\varphi}},\]which is better apparent in the left section of the figure, yet the sine function is defined also for obtuse angles. It further holds that
\[x=\frac{R}{\mathrm{tg}\,{(\pi -\varphi)}}=R\,\mathrm{cotg}\,{(\pi -\varphi)}=-R\,\mathrm{cotg}\,{\varphi}\]and we get by differentiating that
\[\mathrm{d}x=\frac{R}{\sin^2{\varphi}}\,\mathrm{d}\varphi.\]We substitute for the variables in equation (1)
\[B= \frac{\mu_o}{4\pi}\,I \int_\alpha^\beta \frac{R}{\sin^2{\varphi}}\,\frac{\sin^2{\varphi}}{R^2}\sin{\varphi}\,\mathrm{d}\varphi.\]Which yields the equation for calculating the resulting magnetic B-field:
\[B= \frac{\mu_o}{4\pi}\,\frac{I}{R} \int_\alpha^\beta \sin{\varphi}\,\mathrm{d}\varphi.\]We integrate:
\[B= \frac{\mu_o}{4\pi}\,\frac{I}{R}\,[-\cos{\varphi}]_\alpha^\beta,\] \[B= \frac{\mu_o}{4\pi}\,\frac{I}{R}\,(\cos{\alpha}-\cos{\beta}).\]This is the formula for the magnetic B-field of a straight conductor of finite length carrying a current at a general point P.
We move the endpoints A and B to infinity in the case of the straight infinite conductor. This means that α = 0° and β = 180°
\[B= \frac{\mu_o}{4\pi}\,\frac{I}{R}\,(\cos\,0^{\circ}-\cos\,180^{\circ})=\frac{\mu_o}{4\pi}\,\frac{I}{R}\,\left(1-(-1)\right).\]And we get the well known formula for the magnetic B-field of an infinite conductor
\[B= \frac{\mu_o}{2\pi}\,\frac{I}{R}.\]Solution 2
We can also assess the magnitude of the resulting B-field by integrating of the Biot-Savart law over other variables. We show below how to obtain the formula for the magnetic field of the infinite conductor carrying a current at point P by integrating over x.
We segment the lenght of the infinitely long conductor into an infinite number of pieces as indicated in the figure below.
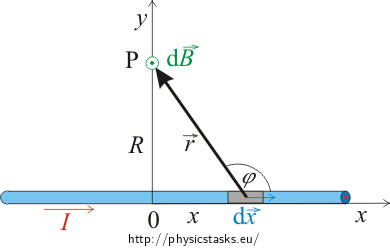
Equation (1) that we have derived in Solution 1 for the magnitude of the magnetic B-field is valid also in this case when we consider that the ends A and B lie in infinity now. Further, it is enough to integrate over one half of the conductor this time:
\[B=\int_{-\infty}^\infty \mathrm{d}B=2\int_0^\infty \mathrm{d}B = \frac{\mu_oI}{2\pi}\, \int_0^\infty\frac{\sin {\varphi}\, \mathrm{d}x}{r^{2}}.\tag{2}\]Variables r, x and angle φ are bound together in this equation by relations that are apparent from the figure. We express r and φ using x in this case.
\[r=\sqrt{x^2+R^2},\] \[\sin{\varphi}=\frac{R}{\sqrt{x^2+R^2}}.\]We substitutes these relations into Equation (2)
\[B=\frac{\mu_oI}{2\pi}\, \int_0^\infty \frac{R}{\sqrt{x^2+R^2}^{3}}\,\mathrm{d}x ,\]and we get by integrating:
\[B=\frac{\mu_oI}{2\pi}\,\left[\frac{x}{R\sqrt{x^2+R^2}}\right]_0^\infty=\frac{\mu_oI}{2\pi R}.\]which is the formula for the magnitude of the B-field of an infinited conductor carrying a current at a general point P, which we wanted to derive.
Note: We must pay attention to express correctly not only the magnitudes of the variables but also their signs.
Answer
The magnitude of the magnetic B-field at any point P in the distance R from the long straight conductor of finite length carrying the current I is:
\[B= \frac{\mu_o}{4\pi}\,\frac{I}{R}\,(\cos{\alpha}-\cos{\beta}).\]A special case is the conductor of infinite length with the ends moved to infinity. The magnitude of the magnetic B-field at any point P in the distance R from the infinitely long straight conductor carrying the current I is:
\[B= \frac{\mu_o}{2\pi}\,\frac{I}{R}.\]