Charged Half-Hoop
Task number: 2317
Find the electric intensity and potential on the axis of a half-hoop using direct integration. The radius of the half-hoop is \(R\). The half-hoop is linearly charged with linear density \(\lambda\). Verify the relation between intensity and potential.
Note: The axis of a half-hoop is considered to be the axis of an imaginary whole hoop.
Similarity with another task
This task is very similar to task Charged Hoop.
Hint: Electric Intensity
Positive point charge Q creates a field of intensity
\[E=\frac{1}{4\pi\epsilon_0} \frac{Q}{r^2}\]in the distance of r.
The vector of intensity \(\vec{E}\) points directly away from the point charge if Q is positive. In the opposite case, the vector points towards the point charge.
Think through how to utilize this piece of information in this task.
Analysis: Electric Intensity
First, we will draw the whole situation into Cartesian coordinates. The axis of the half-hoop will coincide with the z-axis and the half-hoop will lie in the xy-plane. We will also draw two of the cylindrical coordinates \(\alpha\) and z. We will not need the cylindrical coordinate \(\rho\) because the half-hoop has constant diameter R.
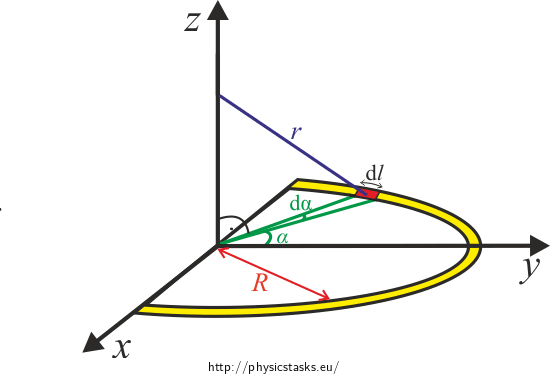
Solution – electric intensity
Positive point charge Q creates a field of intensity
\[{E}=\frac{1}{4\pi\epsilon_0}\frac{Q}{r^2}\]at the distance of r.
If the half-hoop is charged with linear density \(\lambda\), then charge dQ on infinitely small part of the half-hoop dl has the following value \[\textrm{d}Q = {\lambda} {\textrm{d}l},\]
where \(\textrm{d}l=R \textrm{d}\alpha\).
Then
\[\textrm{d}Q =\lambda R \textrm{d}\alpha\]and thus
\[\textrm{d}{E}=\frac{1}{4\pi\epsilon_0} \frac{\textrm{d}Q}{r^2}=\frac{1}{4\pi\epsilon_0} \frac{\lambda R}{r^2}\textrm{d}\alpha.\tag{1}\]Without loss of generality, we can suppose that the hoop is charged positively.
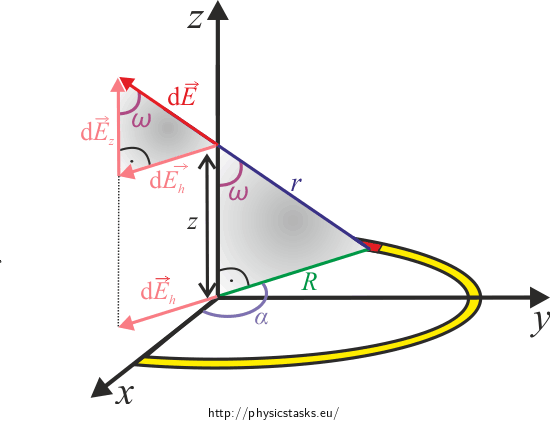
We can express the component of electric intensity \(\textrm{d}E_\mathrm{z}\) using the right angle triangle drawn in the picture and the cosine function:
\[\textrm{d}E_\mathrm{z} = \textrm{d}E\cos\omega.\tag{2}\]The right angle triangles are all similar (according to the AA similarity) and so we can formulate:
\[\cos \omega = \frac{z}{r}.\]We know the following from the Pythagoras theorem
\[r^2 = z^2 + R^2, \tag{3}\]and so we can express the cosine function as
\[\cos \omega= \frac{z}{\sqrt{z^2 + R^2}}.\tag{4}\]By connecting (1),(2),(3) and (4), we receive
\[\textrm{d}E_\mathrm{z} =\frac{1}{4\pi\epsilon_0} \frac{\lambda R z}{(z^2+R^2)^{3/2}}\textrm{d}\alpha.\]We will now integrate this across the whole circumference of the half-hoop, i.e. we will integrate with respect to \(\alpha\):
\[ E_\mathrm{z} =\int_{0}^{\pi} \frac{1}{4\pi\epsilon_0} \frac{\lambda R z}{(z^2+R^2)^{3/2}}\textrm{d}\alpha. \]Distances R and z do not depend on \(\alpha\) and so we can factor them out from the integral:
\[ E_\mathrm{z} =\frac{1}{4\pi \epsilon_0} \frac{\lambda R z}{(z^2+R^2)^{3/2}} \int_{0}^{\pi} \textrm{d}\alpha. \]After integration we obtain
\[ E_\mathrm{z} =\frac{1}{4\epsilon_0} \frac{\lambda R z}{(z^2+R^2)^{3/2}}. \]To determine the remaining components of electric intensity, we need to express the horizontal component of intensity \(E_\mathrm{h}\) the same way.

From the right angle triangle follows that
\[\textrm{d}E_\mathrm{h}=\textrm{d}E \sin\omega.\tag{5}\]Now we know that the triangles are similar according to the AA similarity theorem. We can thus express the sine function as
\[\sin \omega = \frac {R} {r}.\]Once we add the Pythagoras theorem (3), we receive
\[\sin \omega = \frac {R} {\sqrt{z^2 + R^2}}.\tag{6}\]By connecting (1),(3),(5) and (6), we receive
\[\textrm{d}E_\mathrm{h} =\frac{1}{4\pi\epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}}\textrm{d}\alpha. \]Now we will focus on expressing the components of \(E_\mathrm{x}\) and \(E_\mathrm{y}\). For clarity, we will project the whole situation into the xy-plane.
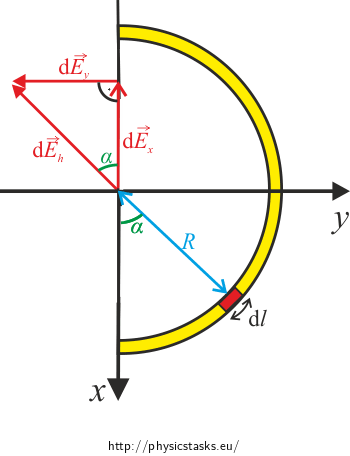
Inspecting the right angle triangle we see that
\[\textrm{d}E_\mathrm{y}=\textrm{d}E_h\sin \alpha,\] \[\textrm{d}E_\mathrm{x}=\textrm{d}E_h\cos \alpha.\]Let us start with \(\textrm{d}E_\mathrm{y}:\)
\[\textrm{d}E_\mathrm{y}=\frac{1}{4\pi\epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}}\sin \alpha \thinspace\textrm{d}\alpha,\]which will be integrated across the whole circumference of the half-hoop, i.e. we will integrate across angle \(\alpha\):
\[E_\mathrm{y}=\int_{0}^{\pi}\frac{1}{4\pi\epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}}\sin \alpha \thinspace\textrm{d}\alpha.\]Distances R and z are independent of \(\alpha\) and so we can factor them out of the integral:
\[E_\mathrm{y}=\frac{1}{4\pi\epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}}\int_{0}^{\pi}\sin \alpha \thinspace\textrm{d}\alpha,\] \[E_\mathrm{y}=\frac{1}{4\pi\epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}}\left[-\cos \alpha \right]_{0}^{\pi},\]thus
\[E_\mathrm{y}=\frac{1}{2\pi\epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}}.\]Now we will calculate \(\textrm{d}E_\mathrm{x}\):
\[\textrm{d}E_\mathrm{x}=\frac{1}{4\pi\epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}}\cos\alpha \thinspace\textrm{d}\alpha,\]which will be integrated across the whole circumference of the half-hoop, i.e. we will integrate across angle \(\alpha\):
\[E_\mathrm{x}=\int_{0}^{\pi}\frac{1}{4\pi\epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}}\cos\alpha \thinspace\textrm{d}\alpha.\]Distances R and z are independent of \(\alpha\) and so we can factor them out of the integral:
\[E_\mathrm{x}=\frac{1}{4\pi \epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}}\int_{0}^{\pi}\cos\alpha \thinspace\textrm{d}\alpha,\] \[E_\mathrm{x}=\frac{1}{4\pi \epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}}\left[\sin \alpha \right]_{0}^{\pi},\] \[E_\mathrm{x}=0,\]which does not surprise us because of the symmetry of the half-hoop.
Hint – potential
We will use the relation for potential of a point charge analogically to the calculation of electric intensity. The potential of a point charge at distance r is
\[φ = \frac{1}{4\pi\epsilon_0}\frac{Q}{r}.\]Think of how to use the relation for calculation of potential on the axis of the half-hoop.
Hint Solution
We will separate the half-hoop into smaller parts that will behave like point charges. We will then obtain the whole potential by “adding up” (or rather by integrating) all contributions of potential of these smaller parts.
First, draw this whole situation into the Cartesian coordinates. The axis of the half-hoop will coincide with the z-axis and the half-hoop will lie in the xy-plane. We will also draw two of the cylindrical coordinates: \(\alpha\) and z. Cylindrical coordinate \(\rho\) will not be needed because the radius of the half-hoop R is constant.

Analysis – potential
First, we draw the whole situation in the Cartesian coordinates. The axis of the half-hoop will coincide with the z-axis and the half-hoop will lie in the xy-plane. We will also draw two of the cylindrical coordinates into the picture: \(\alpha\) and z. The cylindrical coordinate \(\rho\) will not be used because the half-hoop has a constant radius of R.

Solution – potential
Point charge Q causes electric potential of
\[\varphi= \frac{1}{4\pi\epsilon_0} \frac {Q} {r},\]at distance r. If we focus on a single small part of the half-hoop, potential at a point of the axis of the half-hoop caused by the small part is
\[\textrm{d}\varphi= \frac{1}{4\pi\epsilon_0} \frac {\textrm{d}Q} {r}\tag{8}\]and since the half-hoop is charged with linear density \(\lambda\) then
\[\textrm{d}Q=\lambda\textrm{d}l.\]We will also use \(\textrm{d}l=R\thinspace\textrm{d}\alpha\) and obtain
\[\textrm{d}Q=\lambda R\thinspace\textrm{d}\alpha.\tag{9}\]We receive from (8) and (9) the following:
\[\textrm{d}\varphi=\frac{1}{4\pi \epsilon_0} \frac {\lambda R}{r}\textrm{d}\alpha. \tag{10}\]Now we will focus on expressing distance r using parameters of the half-hoop and distance z.
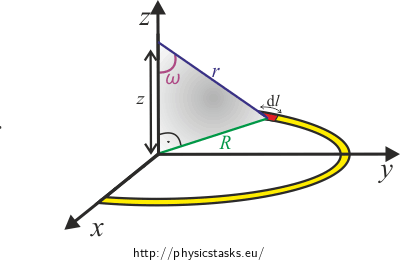
We can express the following from the Pythagoras theorem
\[r = \sqrt{z^2 + R^2}.\tag{11}\]If we combine (10) and (11), we receive
\[\textrm{d}\varphi=\frac{1}{4\pi\epsilon_0} \frac {\lambda R}{\sqrt{z^2 + R^2}}\textrm{d}\alpha, \]which we will integrate across the whole circumference of the half-hoop, i.e. we will integrate across angle \(\alpha\):
\[\varphi=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\frac{1}{4\pi\epsilon_0} \frac {\lambda R}{\sqrt{z^2 + R^2}}\textrm{d}\alpha. \]Distances R and z are independent of \(\alpha\) and so we can factor them out:
\[\varphi=\frac{1}{4\pi\epsilon_0} \frac {\lambda R}{\sqrt{z^2 + R^2}}\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\textrm{d}\alpha, \] \[\varphi=\frac{1}{4\pi\epsilon_0} \frac {\lambda R}{\sqrt{z^2 + R^2}}\bigg[\alpha\bigg]_{-\frac{\pi}{2}}^{\frac{\pi}{2}}, \] \[\varphi=\frac{1}{4\epsilon_0} \frac {\lambda R}{\sqrt{z^2 + R^2}}. \]Note: Potential on the z-axis of a charged half-hoop is the half of the potential of a charged hoop (comparison Charged Hoop, Solution c)). This property applies in general. It is caused by the fact that potential is a scalar function.
Hint – relation proof
Potential and electric intensity are conjoined by an equation in which there is the mathematical operator gradient.
Try to recall or find what relation it is. Recall what gradient is and how it is calculated (in the Cartesian coordinates).
Solution – relation proof
We are supposed to prove the relation from the hint solution
\[\vec{E}=-\thinspace\text{grad}\thinspace\varphi.\]We can conduct the proof only for points lying on the axis of the half-hoop and only for the z component since we determined the dependence of potential on the z coordinate only.
The potential on the axis of the half-hoop is given by
\[\varphi=\frac{1}{4\epsilon_0} \frac {\lambda R}{\sqrt{z^2 + R^2}}. \]The component of the gradient of potential into the direction of the z axis is
\[\frac{\partial{\varphi}}{\partial{z}}=-\frac{1}{2} \frac {1} {\epsilon_0}\frac{\lambda R}{(z^2 + R^2)^{3/2}}2z = - \frac {1} {4\epsilon_0}\frac{\lambda R z}{{(z^2 + R^2)^{3/2}}},\]which yields the z component of electric intensity \(E_\mathrm{z}\) in the same form as the direct calculation done in part a):
\[E_\mathrm{z} =\frac {1} {4\epsilon_0}\frac{\lambda R z}{{(z^2 + R^2)^{3/2}}}.\]Now we will also prove that the reverse relation applies as well:
\[\varphi=-\int_\infty^{{\hat{z}}}{E_\mathrm{z}}\textrm{d}z,\]where we integrate across the \(z\) axis from „infinity“, where the potential is zero, to a point with coordinate \(\hat {z}\).
If we substitute the calculated value \(E_\mathrm{z}\), we obtain
\[\varphi=-\int_\infty^{{\hat{z}}} \ {\frac {1} {4\epsilon_0}\frac{\lambda R z}{{(z^2 + R^2)^{3/2}}}}\textrm{d}z,\] \[\varphi=-{\frac {\lambda R} {4\epsilon_0}\int_\infty^{{\hat{z}}}\frac{ z}{{(z^2 + R^2)^{3/2}}}}\textrm{d}z.\]We will solve the integral by substitution by using
\[R^2 + z^2 = a,\] \[2z \textrm{d}z = \textrm{d}a,\] \[z \rightarrow \infty \Rightarrow a \rightarrow \infty \qquad ; \qquad z = \hat{z} \Rightarrow a = \hat{z}^2 + R^2, \] \[\varphi=-{\frac {\lambda R} {8\epsilon_0}\int_\infty^{{\hat{z}^2 + R^2}}\frac{1 }{{a^{3/2}}}}\textrm{d}a,\] \[\varphi=\frac {\lambda R} {4\epsilon_0} \left[\frac{1}{a^{1/2}}\right]_\infty^{{\hat{z}^2 + R^2}}.\]After substituting the limits, we receive
\[\varphi=\frac {\lambda R} {4\epsilon_0} \frac{1}{(R^2 + \hat{z}^2)^{1/2}} =\frac {1} {4\epsilon_0} \frac{\lambda R}{\sqrt{R^2 + \hat{z}^2}} .\]Since \(\hat {z}\) is an arbitrary point on the z axis, we can leave out the hat and end up with \(z\):
\[\varphi=\frac {\lambda R} {4\epsilon_0} \frac{1}{(R^2 + {z}^2)^{1/2}} =\frac {1} {4\epsilon_0} \frac{\lambda R}{\sqrt{R^2 + {z}^2}},\]which yield the expected relation.
Answer
The electric intensity on the axis of a homogenously charged half-hoop is \[ E_\mathrm{z} =\frac{1}{4\epsilon_0} \frac{\lambda R z}{(z^2+R^2)^{3/2}}, \] \[E_\mathrm{y}=\frac{1}{2\pi \epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}},\] \[E_\mathrm{x}=0.\] The potential on the axis of a homogenously charged half-hoop is \[\varphi=\frac{1}{4\epsilon_0} \frac {\lambda R}{\sqrt{z^2 + R^2}}. \]We also proved the relation between \(\vec {E}\) and φ for points lying on the axis of the half-hoop.
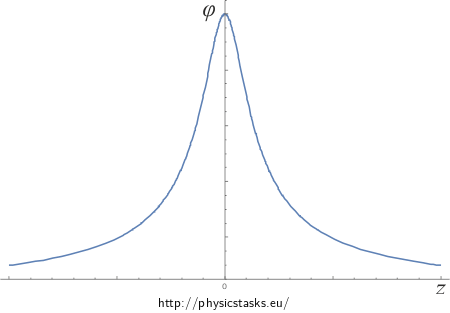
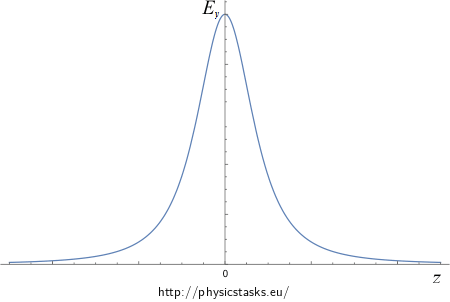
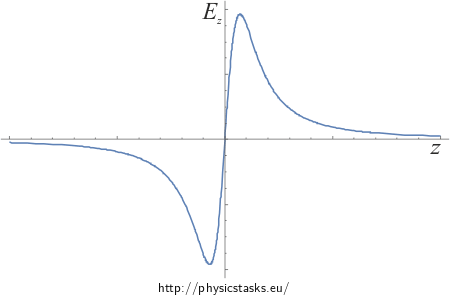
Graphs of course of electric intensity and potential
We can see the course of electric intensity and potential dependence on distance z from the centre of the half-hoop in the following graphs.
Quarter circle and arc with arc angle of β
Quarter circle
The calculation of electric intensity and potential on the z axis has been done for a semicircle. Now we will look at how a quarter circle fares.
We have derived the following equations for a semicircle:
\[ E_\mathrm{z} =\frac{1}{4\pi \epsilon_0} \frac{\lambda R z}{(z^2+R^2)^{3/2}} \int_{0}^{\pi} \textrm{d}\alpha, \] \[E_\mathrm{y}=\frac{1}{4\pi\epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}}\int_{0}^{\pi}\sin \alpha\thinspace\textrm{d}\alpha,\] \[E_\mathrm{x}=\frac{1}{4\pi \epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}}\int_{0}^{\pi}\cos \alpha\thinspace\textrm{d}\alpha.\]The only differences with a quarter circle are the integration limits:
\[ E_\mathrm{z} =\frac{1}{4\pi \epsilon_0} \frac{\lambda R z}{(z^2+R^2)^{3/2}} \int_{0}^{\frac{\pi}{2}} \textrm{d}\alpha, \] \[E_\mathrm{y}=\frac{1}{4\pi\epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}}\int_{0}^{\frac{\pi}{2}}\sin \alpha\thinspace\textrm{d}\alpha,\] \[E_\mathrm{x}=\frac{1}{4\pi \epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}}\int_{0}^{\frac{\pi}{2}}\cos \alpha\thinspace\textrm{d}\alpha.\]We receive the following after integration
\[ E_\mathrm{z} =\frac{1}{8 \epsilon_0} \frac{\lambda R z}{(z^2+R^2)^{3/2}}, \] \[E_\mathrm{y}=\frac{1}{4\pi\epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}},\] \[E_\mathrm{x}=\frac{1}{4\pi \epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}}.\]We have also derived the following in a similar manner for potential of a semicircle
\[\varphi=\frac{1}{4\pi\epsilon_0} \frac {\lambda R}{\sqrt{z^2 + R^2}}\int_{0}^{\pi}\textrm{d}\alpha. \]The only difference with a quarter circle is the integration limit:
\[\varphi=\frac{1}{4\pi\epsilon_0} \frac {\lambda R}{\sqrt{z^2 + R^2}}\int_{0}^{\frac{\pi}{2}}\textrm{d}\alpha. \]We obtain the following after integration
\[\varphi=\frac{1}{8\epsilon_0} \frac {\lambda R}{\sqrt{z^2 + R^2}}. \]Arc with arc angle of \(\beta\)
We will use the derived results again. We will replace the particular angle in the integration limits with a general one denoted as \(\beta\):
\[ E_\mathrm{z} =\frac{1}{4\pi \epsilon_0} \frac{\lambda R z}{(z^2+R^2)^{3/2}} \int_{0}^{\beta} \textrm{d}\alpha, \] \[E_\mathrm{y}=\frac{1}{4\pi\epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}}\int_{0}^{\beta}\sin \alpha\thinspace\textrm{d}\alpha,\] \[E_\mathrm{x}=\frac{1}{4\pi \epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}}\int_{0}^{\beta}\cos \alpha\thinspace\textrm{d}\alpha,\] \[\varphi=\frac{1}{4\pi\epsilon_0} \frac {\lambda R}{\sqrt{z^2 + R^2}}\int_{0}^{\beta}\textrm{d}\alpha. \]We obtain this after integration
\[ E_\mathrm{z} =\frac{\beta}{4\pi \epsilon_0} \frac{\lambda R z}{(z^2+R^2)^{3/2}} , \] \[E_\mathrm{y}=\frac{1}{4\pi\epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}}(-\cos\beta +1),\] \[E_\mathrm{x}=\frac{1}{4\pi \epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}}\sin\beta,\] \[\varphi=\frac{\beta}{4\pi\epsilon_0} \frac {\lambda R}{\sqrt{z^2 + R^2}}. \]Comment – dependence on angle β
If we compare the z component of electric intensity of a semicircle, quarter circle and an arc of arc angle \(\beta\), we can see that this component of electric intensity is proportional to the size of the arc. In the case of a semicircle, the arc angle is \(\beta =\pi\) and quarter circle \(\beta = \frac{\pi}{2}\).
Semicircle:
\[ E_\mathrm{z} =\frac{1}{4\epsilon_0} \frac{\lambda R z}{(z^2+R^2)^{3/2}}. \]Quarter circle:
\[ E_\mathrm{z} =\frac{1}{8 \epsilon_0} \frac{\lambda R z}{(z^2+R^2)^{3/2}}. \]Arc with arc angle of \(\beta\):
\[ E_\mathrm{z} =\frac{\beta}{4\pi \epsilon_0} \frac{\lambda R z}{(z^2+R^2)^{3/2}}. \]By comparing the potentials, we reach the same conclusion.
Semicircle:
\[\varphi=\frac{1}{4\epsilon_0} \frac {\lambda R}{\sqrt{z^2 + R^2}}. \]Quarter circle:
\[\varphi=\frac{1}{8\epsilon_0} \frac {\lambda R}{\sqrt{z^2 + R^2}}. \]Arc with arc angle of \(\beta\):
\[\varphi=\frac{\beta}{4\pi\epsilon_0} \frac {\lambda R}{\sqrt{z^2 + R^2}}. \]The x and y components of electric intensity do not yield the same proportionality.
The potential and the z component of electric intensity are both proportional to the size of the arc angle that is charged since every charged „tiny bit“ of the hoop adds up to the total value the same amount. Since the x and y components of electric intensity add up differently, they are sometimes positive, sometimes negative. This is the reason why the x and y components of electric intensity cannot be proportional to the size of the arc.




