Electrical Pendulum in Charged Sphere’s Field (Big Deflection)

Task number: 2139

Let us use an electrostatic pendulum to measure the amount of an unknown electric charge.

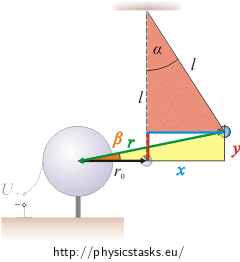
The electrostatic pendulum is a small conductive ball hanging vertically on an insulating string next to a bigger conductive sphere that is placed on an insulating stand. The length of our string is \(l=12\,\mathrm{cm}\), the weight of the small ball is m = 0.6 g, the radius of the bigger sphere is \(R=2\,\mathrm{cm}\) and the distance between the centers of the ball and the sphere in uncharged state is \(r_0 = 5\,\mathrm{cm}\).

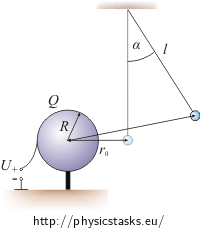
We put the unknown charge on the small ball and then we connect the bigger sphere to the positive clamp of a source of a voltage \(V=22\,\mathrm{kV}\) and we earth the other clamp of the source. The small ball gets displaced away from the sphere until it hangs at an angle of \(\alpha=25°\) from the vertical. It is clear from the repulsive reaction of the balls, that the charges on them have the same polarity.

a) What is the magnitude of the electric force acting on the pendulum ball? What is the magnitude of tension of the string?

b) What amount of electric charge \(Q\) will be collected on the sphere after we connect it to the voltage source? What is the unknown amount of electric charge \(q\) stored on the pendulum ball?

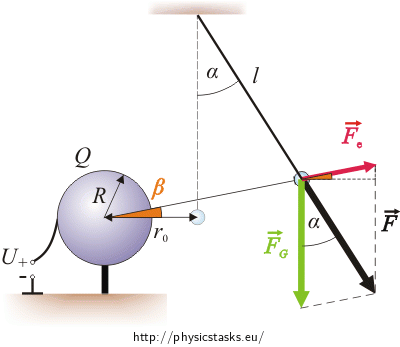
Sketch of forces acting on the pendulum
Hint

Though it is not obvious from the assignment, we will require the angle β for further calculations. We will express it using trigonometric functions.
a) Hint: Expression of the electrical force
Focus on the blue triangle.

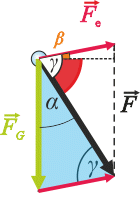
Use the sine law and express the ratio of electrical and gravitational force.

Comment:

The sine law is in the section Used mathematical formulae.
Calculation of the angle β

We need to know the angle β for further calculations. We will calculate it in this section for clarity.

We will express the angle β from the yellow right-angle triangle.
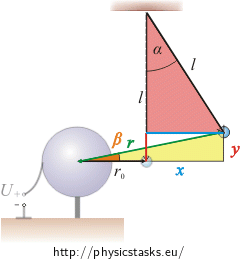
\[\mathrm{tg}\,\beta \,=\,\frac{y}{r_0+x}\tag{1}\]
The distances x and y will be calculated from the red triangle using trigonometric functions as well:
\[x\,=\,l\sin\alpha\] \[y\,=\,l-l\cos\alpha\,=\,l\left(1-\cos\alpha\right)\,\]
and we will substitute into formula (1).
\[\mathrm{tg}\,\beta \,=\,\frac{l\left(1-\cos\alpha\right)}{r_0+l\sin\alpha}\]
a) Calculation of the electrical force

Forces acting on the ball are the gravitational force \(\vec{F}_G\) and repulsive electrical force \(\vec{F}_e\). The resultant of these forces if the force \(\vec{F}\) which the ball stretches the string with.

We will calculate the electrical force from the blue triangle using the sine law.
\[\frac{F_e}{F_G}\,=\,\frac{\sin \alpha}{\sin\gamma}\] \[F_e\,=\,\frac{F_G\,\sin \alpha}{\sin\gamma}\tag{*}\]
Now we will express the angle γ using known angles α and β. We can see two identical triangles in the picture (blue and white). The angle γ is also in the white triangle and thus we can express it as the sum of the red angle 90° - α and the angle β.

γ = 90° – α + β

The angle β was calculated in the previous section (Calculation of the angle β).

We will substitute the angle γ into the equation (*) and we will adjust the equation.
\[F_e\,=\,\frac{F_G\,\sin \alpha}{\sin\left(90^{\circ}-\alpha+\beta\right)}\,=\,\frac{F_G\,\sin \alpha}{\sin\left(90^{\circ}-\left(\alpha-\beta\right)\right)}\] \[F_e\,=\,\frac{F_G\,\sin \alpha}{\cos\left(\alpha-\beta\right)}\]
Now we only need to substitute for the gravitational force F_G = mg.
\[F_e\,=\,\frac{mg\,\sin \alpha}{\cos\left(\alpha-\beta\right)}\]
a) Hint: Formulation of the force that stretches the string

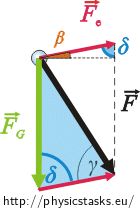
Using the sine law in the blue triangle, express the ratio of the force that stretches the ball and the gravitational force.

Note:

The sine law is in the section Used mathematical formulae.
a) Calculation of the force through which the ball stretches the string

The force \(\vec{F}\), through which the ball of the pendulum stretches the string, can be calculated similarly to electrical force using the sine law.
\[\frac{F}{F_G}\,=\,\frac{\sin \delta}{\sin\gamma}\] \[F\,=\,\frac{F_G\,\sin \delta}{\sin\gamma}\]
We substitute for angles γ and δ using known angles α and β.

The angle γ was formulated in sectrion Calculation of the electrical force.

γ = 90° – α + β

The angle δ will be expressed using the angle β (see pic.)

δ = 90° – β .
\[F\,=\,\frac{F_G\,\sin \left(90^{\circ}-\beta\right)}{\sin\left(90^{\circ}-\alpha+\beta\right)}\]
We adjust the numerator and denominator of the fraction.
\[F\,=\,\frac{F_G\,\cos \beta}{\cos\left(\alpha-\beta\right)}\]
We substitute for the gravitational force F_G = mg and we receive a relation for calculation of the force F through which the ball stretches the string.
\[F\,=\,\frac{mg\,\cos\beta}{\cos\left(\alpha-\beta\right)}\]
b) Hint: Calculation of the charge on the sphere and the ball of the pendulum
Calculation of the charge on the sphere:

The sphere is conductive, thus the charge from the power source will shift its charge onto the sphere untill the surface of the sphere has the same potential as the power source.

Calculation of the charge on ball of the pendulum:

For this calculation, use the calculated electrical force and Coulomb’s law.
b) Analysis: Calculation of the charge on the sphere and on the ball of the pendulum
The potential on the surface of the conductive sphere is the same as the potential of the power source. If the potentials were different, the charge would start to move onto the sphere (or vice versa). The charge would move until the potentials balanced out.

One clip of the power source is grounded and so the voltage of the source is the same as the potential of the not-grounded clip. The potential around the sphere that is charged on the surface is the same as potential around a mass point (it’s directly dependent on the charge of the sphere and indirectly dependent on the distance from the sphere’s centre).

Electrical force is acting on the ball of the pendulum according to Coulomb’s law. The force is directly dependent on the charge of the ball and the sphere and indirectly dependent on the square of the distance between the ball and the sphere. If we express the distance between the centres of the ball and the sphere, we can determine the ball’s charge using Coulomb’s law.
b) Calculation of the charge on the sphere
The sphere is conductive so the whole electrical charge will be on its surface.

The same relation applies for both the sphere with charge on its surface and the mass point:
\[\varphi\,=\,\frac{1}{4\pi\varepsilon_0}\,\frac{Q}{R}\]
The potential on the sphere’s surface is equal to the voltage to which the sphere is connected. If the potential were different, charge would move from the power source to the sphere (of vice versa) until the potentials balanced out.
\[U\,=\,\varphi\,=\,\frac{1}{4\pi\varepsilon_0}\,\frac{Q}{R}\]
Now we only need to express the wanted charge Q.
\[Q\,=\,4\pi\varepsilon_0 U R \tag{**}\]
b) Calculation of the charge on the ball of the pendulum
The charge that we moved onto the ball of the pendulum can be calculated using the Coulomb’s law.
\[F_e\,=\,\frac{1}{4\pi\epsilon_0} \,\frac{Qq}{r^2}\]
We express the wanted charge q.
\[q\,=\,\frac{4\pi\varepsilon_0 F_e r^2 } {Q}\]
We substitute for the charge Q from relation (**)
\[Q\,=\,4\pi\varepsilon_0 U R \,,\]
that we expressed in the previous part of the task (Calculation of the charge on the sphere)

\[q\,=\,\frac{4\pi\varepsilon_0 F_e r^2 } {4\pi\varepsilon_0 U R}\,=\,\frac{F_e r^2 } {U R}\]
The distance r can be calculated using the yellow triangle
\[\sin\beta\,=\,\frac{y}{r}\] \[r\,=\,\frac{y}{\sin\beta}\,=\,\frac{l\left(1-\cos\alpha\right)}{\sin\beta}\]
and we substitute into the relation for calculation of the charge q.
\[q\,=\,\frac{F_e l^2\left(1-\cos\alpha\right)^2 } { U R\sin^2\beta}\]

We also substitute for the electrical force \(F_e\,=\,\frac{mg\,\sin \alpha}{\cos\left(\alpha-\beta\right)}\), that we calculated in the section Calculation of the electrical force.
\[q\,=\,\frac { mg l^2\left(1-\cos\alpha\right)^2\sin \alpha } { U R\cos\left(\alpha-\beta\right)\sin^2\beta}\]

List of known information and numerical calculation

U = 22 kV = 2.2·10⁴ V	F_e = ? (N)
m = 0.6 g = 6·10⁻⁴ kg	F = ? (N)
l = 12 cm = 0.12 m	Q = ? (C)
R = 2 cm = 2·10⁻² m	q = ? (C)
r₀ = 5 cm = 5·10⁻² m	From tables:
α = 25°	g = 9.8 ms⁻²
	ε₀ = 8.85·10⁻¹² C²N⁻¹m⁻²

Calculation of the angle β \[\mathrm{tg}\,\beta \,=\,\frac{l\left(1-\cos\alpha\right)}{r_0+l\sin\alpha}\,=\,\frac{0.12\,\cdot\left(1-\cos\, 25^\circ\right)}{0.05 \,+\,0.12\cdot\sin\, 25^\circ}\] \[\beta \,=\,6.37^\circ\] Calculation of the electrical force: \[F_e\,=\,\frac{mg\,\sin \alpha}{\cos\left(\alpha-\beta\right)} \,=\,\frac{6 {\cdot} 10^{-4} \cdot 9.8\cdot\,\sin 25^\circ}{\cos\left(25^\circ-6.37^\circ\right)}\,\mathrm{N}\,=\,2.6 {\cdot} 10^{-3}\,\mathrm{N} \] Calculation of the force of the ball: \[F \,=\,\frac{mg\,\cos\beta}{\cos\left(\alpha-\beta\right)}\,=\,\frac{6 {\cdot} 10^{-4}\cdot 9.8\cdot\,\cos 6.37^\circ}{\cos\left(25^\circ-6.37^\circ\right)}\,\mathrm{N}\,=\,6.2 {\cdot} 10^{-3}\,\mathrm{N}\] Calculation of the charge on the sphere: \[Q\,=\,4\pi\varepsilon_0 U R \, =\,4\pi\cdot 8.85 {\cdot} 10^{-12}\,\cdot\,2.2{\cdot} 10^{4}\,\cdot\, 2{\cdot} 10^{-2}\,\mathrm{C}\] \[Q\,=\,4.9{\cdot} 10^{-8}\,\mathrm{C}\] Calculation of the charge on the ball of the pendulum: \[q\,=\,\frac { mgl^2\left(1-\cos\alpha\right)^2 \sin \alpha} { U R\cos\left(\alpha-\beta\right)\sin^2\beta} \] \[q\,=\,\frac { 6 {\cdot} 10^{-4}\,\cdot 9.8\, \cdot 0.12^2\cdot\left(1-\cos25^\circ\right)^2\sin 25^\circ } { 2.2{\cdot} 10^{4}\,\cdot\, 2{\cdot} 10^{-2}\cdot\cos\left(25^\circ-6.37^\circ\right)\cdot\sin^2 6.37^\circ}\,\mathrm{C}\,=\,6.1{\cdot} 10^{-8}\,\mathrm{C}\]

Answer
The electrical force acting on the ball of the pendulum is
\[F_e\,=\,\frac{mg\,\sin \alpha}{\cos\left(\alpha-\beta\right)}\,=\,2.6 {\cdot} 10^{-3}\,\mathrm{N}\]
and the ball stretches the string with force of
\[F \,=\,\frac{mg\,\cos\beta}{\cos\left(\alpha-\beta\right)}\,=\,6.2 {\cdot} 10^{-3}\,\mathrm{N}\,.\]
After connecting the power source onto the sphere, charge of \[Q\,=\,4\pi\epsilon_0 U R \,=\,\,4.9{\cdot} 10^{-8}\,\mathrm{C}\, \] will appear.

We transfered charge of \[q\,=\,\frac { mgl^2\left(1-\cos\alpha\right)^2 \sin\alpha} { U R\cos\left(\alpha-\beta\right)\sin^2\beta}\,=\,6.1{\cdot} 10^{-8}\,\mathrm{C}\,.\] onto the ball.
Used mathematical formulae
This relation applies between trigonometric functions:
\[\sin {\left(90^\circ - \varphi\right)}\,=\, \cos \varphi \]
We used this relation in this task in sections Calculation of the electrical force and Calculation of the tension of the string:
\[\sin {\left(90^\circ - \alpha+\beta\right)}\,=\,\sin {\left(90^\circ -\left( \alpha-\beta\right)\right)}\,=\, \cos{\left( \alpha - \beta \right)}\]
The sine law:

The ratio of the lengths of the sides of a triangle is equal to the ratio of sines of the opposite angles.
\[\frac{a}{b}\,=\,\frac{sin\alpha}{sin\beta}\]
Link to an easier task
If the ball were repulsed by only a small angle, we would be able to neglect the angle β. This case is solved in task Elektrické kyvadélko v poli nabité koule (malá výchylka) (not translated yet).