Wired square
Task number: 2341
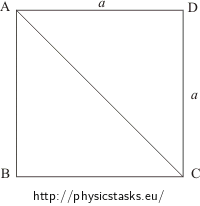
Determine the electrical resistance of a wired square with diagonal for two cases:
a) Square is connected to the power at points A, C.
b) Square is connected to the power at points B, D.
Square is made out of homogenous wire. Let’s mark the length of one side a, cross–section of the wire S and resistivity ρ.
Hint 1
Draw resistors of corresponding resistance “on the wires“ and then redraw this schematic in a more “common“ way. “Deformation“ of the wires does not change the characteristics of the circuit.
Hint 2
Realize how the resistance of a homogenous wire can be calculated.
Breakdown
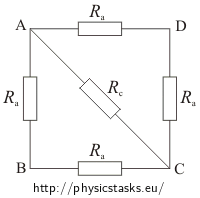
In order to imagine this situation easily we will add on every line segment a resistor with a corresponding resistance. In this new schematic we will consider the wires to have zero resistance.
Ra corresponds to value of resistance of a wire with length a,
Rc corresponds to value of resistance of a wire with length c, where c is the diagonal in this square with side a.
We will redraw the circuit in a “more common“ way according to the connection to power.
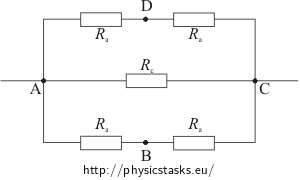
a) Square is connected at points A, C.
We will use the fact that with resistors in series the total resistance is equal to sum of the resistances of each resistor. If they are in parallel the reciprocal value of total resistance is equal to the sum of reciprocal values of resistance in individual branches.
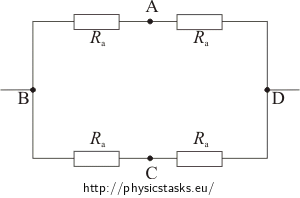
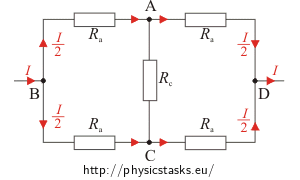
b) Square is connected at points B, D.
Let’s imagine current I flows into the knot B. Because this circuit is symmetrical the current I will divide in half into both branches. Also from point D current I flows out and thanks to symmetry we can say that the currents flowing through branches CD and AD are the same. Their value is equal to one half of the current I.
From knot B to knot A flows in current \(\frac{I}{2}\), from knot A to D flows out \(\frac{I}{2}\). Because the sum of currents flowing in the knot is the same as sum of currents flowing out of the knot there is no current left to flow through resistor Rc so we can leave it out.
For calculating the total resistance we will use the same laws as in part a).
Solution of part a)
If the wired square is connected to the power at points A and C we can redraw the integration in this way:
where \(R_a\,=\, \rho\frac{a}{S} \), \(R_{c}\,=\, \rho\frac{c}{S}\,. \)
c is the value of length of diagonal in square with side a, therefore
\[c\,=\,a \sqrt{2}\] \[R_c\,=\, \rho\frac{a\sqrt{2}}{S}\,.\]In our case this means we can calculate the total resistance from this equation
\[\frac{1}{R}\,=\, \frac{1}{R_a+R_a}+\frac{1}{R_c}+\frac{1}{R_a+R_a}\,.\]We can modify this equation:
\[\frac{1}{R}\,=\, \frac{1}{2R_a}+\frac{1}{R_c}+\frac{1}{2R_a}\] \[\frac{1}{R}\,=\, \frac{2}{2R_a}+\frac{1}{R_c}\] \[\frac{1}{R}\,=\, \frac{R_c+R_a}{R_aR_c}\,.\]For total resistance we got this equation:
\[R\,=\, \frac{R_aR_c}{R_c+R_a}\,.\]Now we can substitute \(R_a\,=\, \rho\frac{a}{S} \), \(R_{c}\,=\, \rho\frac{a\sqrt{2}}{S}\,: \)
\[ R\,=\, \frac{\left(\rho\frac{a}{S}\right) \cdot \left(\rho \frac{a\sqrt{2}}{S}\right)}{\rho\frac{a\sqrt{2}}{S} +\rho\frac{a}{S} }\,=\, \frac {\sqrt{2}{\left(\rho\frac{a}{S}\right)}^2} {\left(\sqrt{2}+1\right)\rho\frac{a}{S}} \,=\, \frac{\sqrt{2}\rho\frac{a}{S}}{\left(\sqrt{2}+1\right)}\] \[R\,=\, \frac{\sqrt{2}}{\sqrt{2}+1}\cdot \rho\frac{a}{S} \hspace{20px}|\,\cdot \frac{\sqrt{2}-1}{\sqrt{2}-1}\] \[R\,=\, \frac{2-\sqrt{2}}{2-1}\cdot \rho\frac{a}{S}\,.\]Final formula:
\[R\,=\, \left(2-\sqrt{2}\right) \rho\frac{a}{S}\,.\]Solution of part b)
If the wired square is connected to the power at points B and D we can redraw the integration in this way:
This wiring is symmetrical therefore the current that flows through branches BA, BC, AD and CD is the same. There is no current flowing through resistor Rc. This resistor does not affect the total resistance of the integration. Because of these previous statements we can leave out the branch with resistor Rc:
We have a much easier schematic now and we can easily calculate the total resistance of the integration:
\[\frac{1}{R}\,=\, \frac{1}{\left(R_a+R_a\right)}+\frac{1}{\left(R_a+R_a\right)}\] \[\frac{1}{R}\,=\, \frac{1}{R_a}\,.\]Total resistance of the wired square connected to the power at points C, D is:
\[R\,=\,R_a\,,\]where Ra is electrical resistance of wire with length a
\[R_a\,=\, \rho\frac{a}{S}\,. \]Answer
If the wired square is connected to the power at points A, C its total resistance is \(R\,=\, \left(2-\sqrt{2}\right) \rho\frac{a}{S}\).
If the wired square is connected to the power at points B, D its total resistance is \(R\,=\, \rho\frac{a}{S}\).
Other options how to solve part b)
In case when we would not have found out the “trick“ with same currents and option to leave out the resistor through which there was no current flowing we could solve this problem with Kirchhoff’s laws (see for example assignment Application of Kirchhoff’s laws for calculation of total resistance in a circuit) or with transformation of the triangle to the star (for example Transformace trojúhelník - hvězda; in Czech only). We would proceed in this way also if we had rectangle instead of square.
Other option is solving this problem with knots with the same potential. If there is no current flowing between two points of the circuit (or it won’t be flowing after we connect them) it means that there is no voltage between them, so both points have same potential. These points in integration can be disconnected or connected without changing the total resistance of the integration.
Link to a similar problem
Similar but more complicated assignment calculating the total resistance of the circuit is The resistance of a wire cube. This problem is solved with the help of knots with the same potential.