Field Of Evenly Charged Sphere
Task number: 2320
Charge with volumetric density ρ is equally placed in a sphere will diameter R.
a) Find the intensity of electric field in distance z from the centre of the sphere.
b) Determine the electric potential of the sphere in distance z.
Consider the field to be both inside and outside the sphere. That means that you should find the course of electric intensity and potential for z between „zero and infinity“.
Hint: Electric Field Intensity
We will choose the surface of a sphere with diameter z and centre in the centre of the charged sphere as the Gauss area. In this case, the vector of electric intensity is perpendicular to the Gauss area and has the same size (See section How to Choose Gauss Area?).
We will separate the task into two parts:
- The diameter of the Gauss sphere is bigger than the diameter of the charged sphere.
- The diameter of the Gauss sphere is smaller than the diamter of the charged sphere.
Hint: Electric Potential
Potential energy is equal to the negatively taken work which must be done by the electric force to move charge from place with zero potential to a given spot.
\[E_p(z)\,=\, - \int^z_{\infty} \vec{F} \cdot \mathrm{d}\vec{z}\]Potential is potential energy considered for a unit charge:
\[\varphi\,=\, \frac{E_p}{Q}\,.\]We will substitute the integral.
\[\varphi\,=\, - \int^z_{\infty} \frac{\vec{F}} {Q}\cdot \mathrm{d}\vec{z}\]If we divide the force by charge, we obtain electric field intensity.
\[\varphi\,=\, - \int^z_{\infty} \vec{E}\cdot \mathrm{d}\vec{z}\]Hint: Potential Inside the Sphere
Attention! We are calculating work done by electric force when it moves charge from infinity. We substitute the electric field intensity into the integral. The intensity does not always have the same expression inside and outside the sphere. Therefore, we need to separate the integral into two parts.
Analysis
We will separate the task into two parts. We will look into the field inside the sphere and outside the sphere separately.
Since the charge is spread symetricly across the whole sphere, the simpliest way of finding the electric field intensity will be using the Gauss theorem which expresses the relation between electric intensity flow through a closed area and the total charge inside the closed area.
The vector of electric intensity points away from the centre of the sphere in all points and its size depends on the distance from the centre of the sphere only. The reason for this is the symetrical spreading of charge inside the sphere. The following idea can help us. The charge inside the sphere is spread symetrically and thus there is no difference if we rotate the sphere around axes going through the centre of the sphere. The field around the sphere has to stay the same at all times and thus all the vectros of intensity have to be the same in a single spot with arbitrary sphere rotation.
We will choose a sphere centred at the cetre of the charged sphere as the Gauss area. In this case the vector of electric intensity will be of the same size at every point of the Gauss sphere and will be perpendicular to the surface of the sphere. This will simplify the scalar product calculation and the integral calculation as well.
If we calculate the intensity outside the sphere, the Gauss sphere will have a larger radius than the charged sphere. All charge will be spread inside the Gauss sphere and we will express it usinng the charge density and the charged sphere volume.
If we calculate the intensity inside the sphere, the Gauss sphere will have a smaller radius than the charged sphere. We will express the charge inside the Gauss sphere using the Gauss sphere radius and charge density .
Potential of the electric field can be calculated from the potential energy. The potential energy at a given point is equal to the negative work done by the electric force when moving a charge from a zero potential point to our given point (we will set the zero potential in infinity). Potential is the potential energy of a unit charge.
We have to be careful during the inner potential calculation as the intensity is expressed differently outside and inside the sphere. We will have to separate the work done into two parts. One will be the movement of a charge to the surface of the charged sphere and one will be the movement of the charge inside the sphere.
Solution: Intensity Outside the Sphere
Now we will determine the intensity outside the charged sphere (for z>R).
We will use the Gauss theorem:
\[\oint_S \vec{E} \cdot \mathrm{d}\vec{S}\,=\, \frac{Q}{\varepsilon_0}\] \[\oint_S \vec{E} \cdot \vec{n}\mathrm{d}S\,=\, \frac{Q}{\varepsilon_0}\tag{*}\]The charge is spread out in the sphere symmetrically and therefore the electric field around the sphere is spread symmetrically. The vector of electric intensity points away from the centre of the sphere in all points (i.e. the vector is perpendicular to the surface of the sphere) and its size depends only on the distance from the centre of the sphere.
We will select the surface of a sphere with radius z and centre in the centre of the charged sphere as the Gauss area. In this case the vector of electric intensity will always be perpendicular to the surface of the Gauss area. Therefore, this applies: \(\vec{E} \cdot \vec{n}\,=\,En\,=\,E\) (note \(\vec{n}\) is a unit vector).
Using these pieces of knowledge, we will adjust the integral on the left side of the Gauss theorem:
\[\oint_k \vec{E} \cdot \vec{n}\mathrm{d}S\,=\,\oint_k E n\mathrm{d}S\,=\, \oint_k E\mathrm{d}S\,.\]Electric intensity vector size E is the same at all points of the chosen Gauss area and thus we can factor it out of the integral just like a constant. We then receive the following relation:
\[\oint_k \vec{E} \cdot \vec{n}\mathrm{d}S\,=\,E \oint_k \mathrm{d}S\,.\]We will calculate the integral now. If we integrate dS across the surface of a sphere, we receive the area of the surface of the sphere. (Hint: We can imagine it as if dS were area of small bits of the surface of the sphere. If we add up all these bits, we receive the area of the whole surface of the sphere.) The integral is thus equal to
\[\oint_k \vec{E} \cdot \vec{n}\mathrm{d}S\,=\,E S_k\,,\]where Sk = 4πz2 is the surface of the Gauss sphere.
\[\oint_k \vec{E} \cdot \vec{n}\mathrm{d}S\,=\,E\, 4 \pi z^2\]We will substitute the result back into the Gauss theorem(*).
\[E 4 \pi z^2\,=\, \frac{Q}{\varepsilon_0}\]We will express the value of the intensity.
\[E \,=\, \frac{1}{4 \pi \varepsilon_0}\,\frac{Q}{z^2}\tag{**}\]The equation is the same as for electric field intensity around a point charge. The field around a charged sphere is thus the same as the field around a point charge.
Now we just have o express charge Q inside the selected Gauss area using known quantities.
The whole charged sphere is inside the area. We can thus express the charge using its volume V and volumetric charge density ρ.
\[Q\,=\,V \varrho\,=\,\frac{4}{3} \pi R^3 \varrho\]We will substitute into (**) and adjust.
\[E \,=\, \frac{1}{4 \pi \varepsilon_0}\,\frac{\frac{4}{3} \pi R^3 \varrho}{z^2}\,=\, \frac{\varrho R^3}{3 \varepsilon_0\,z^2}\]The electric field intensity of the charged sphere is equal to:
\[E \,=\, \frac{\varrho R^3}{3 \varepsilon_0} \, \frac{1}{z^2} \,.\]in distance z.
Solution: Intensite Inside Charged Sphere
We will express the intensity of the electric field inside the charged sphere. The method is very similar to the one in the previous section: Intensity outside the sphere and so it is not commented in detail.
We will calculate the electric intensity using the Gauss theorem:
\[\oint_k \vec{E} \cdot \mathrm{d}\vec{S}\,=\, \frac{Q_1}{\varepsilon_0}\,,\tag{*}\]where Q1 is the charge inside the Gauss area.
We will choose the Gauss area to be a sphere with the same centre as the charged sphere and radius of z < R.
We will calculate the integral on the left side of the equation the same way like in the previous section.
\[\oint_k \vec{E} \cdot \vec{n} \mathrm{d}S\,=\, \frac{Q_1}{\varepsilon_0}\,,\]Using the same reasoning about symmetry like in the previous section, we determine that the vector of intensity has the same size at all points of the area and it is perpendicular to the Gauss area. The following then applies:
\[\oint_k \vec{E} \cdot \mathrm{d}\vec{S}\,=\,\oint_k En \mathrm{d}S\,=\,\oint_k E \mathrm{d}S\,=\,E\oint_k \mathrm{d}S.\]The integral is equal to the surface of the Gasuss sphere.
\[\oint_k \vec{E} \cdot \mathrm{d}\vec{S}\,=\,E S_k\] \[\oint_k \vec{E} \cdot \mathrm{d}\vec{S}\,=\,E\, 4 \pi z^2\,\]We will substitute the result back into the Gauss theorem (*)
\[E\, 4 \pi z^2\,=\, \frac{Q_1}{\varepsilon_0}\tag{***}\]Now we will express charge Q1. Only a part of the total charge is located inside the Gauss sphere since its radius is smaller than the radius of the charged sphere. Because of this, we will express the charge using the given charge density and the volume of the Gauss sphere:
\[Q_1\,=\,V_k \varrho \,=\, \frac{4}{3} \pi z^3 \varrho \]We substitute into relation (***).
\[E \,4\pi z^2 \,=\, \frac{\frac{4}{3} \pi z^3\varrho}{\varepsilon_0}\]We adjust and obtain the size of the intensity of the electric field inside the charged sphere:
\[E \,=\, \frac{\varrho}{3 \varepsilon_0}\,z\] Note:If we wanted to express the intensity using the total charge of the sphere Q, we would utilize the fact that the charge is spread equally across the whole sphere and thus the part of charge inside the Gauss sphere is proportional to its volume. \[\frac{Q_1}{Q}\,=\,\frac{4\pi z^3 \varrho }{4\pi R^3 \varrho }\,=\,\frac{z^3}{R^3} \hspace{20px} \Rightarrow \hspace{20px}Q_1\,=\,Q\,\frac{z^3}{R^3} \]The following then applies for the intensity:
\[E \,=\,\frac{Q}{4 \pi \varepsilon_0 R^3}\,z\,.\]It can be seen from the resulting equation that the value of electric intensity in the centre of the sphere is zero and it grows with increasing distance from the centre of the sphere.
Solution: Potential Outside The Charged Sphere
The potential energy in point A is equal to the negative work done by the electric force to move a charge from a point with zero potential to point A. We will choose the zero potential point in infinity.
\[E_{pA}\,=\, - \int_{\infty}^A \vec{F} \cdot \mathrm{d}\vec{r}\]We will express the electric force using the charge size and the electric field intensity.
\[E_{pA}\,=\, - Q \int_{\infty}^A \vec{E} \cdot \mathrm{d}\vec{r}\]The potential of an electric field is the potential energy of a unit charge. We thus obtain the following for calculation of the potential at point A:
\[\varphi_A\,=\,\frac{E_{pA}}{Q}\,=\, - \int_{\infty}^A \vec{E} \cdot \mathrm{d}\vec{r}\,.\]Since the intensity of the electric field is dependent on the distance from the centre of the sphere only, potential of the electric field also depends on distance z from the centre of the sphere.
\[\varphi (z)\,=\, - \int_{\infty}^z \vec{E} \cdot \mathrm{d}\vec{z}\]The potential is independent of the integration path and so we can choose any path we want (we will choose the most simple one). In this case, we will choose the path to be a line segment that points to the centre of the sphere.
Vector of electric intensity \(\vec{E}\) is parallel to vector \(\vec{z}\) and so we can simplify the integral.
\[ \varphi (z)\,=\, - \int^{z}_{\infty} E \mathrm{d}z \]Now we have to split the task into two cases and calculate the integral outside and inside the sphere seperately.
First we express the potential at distance z outside the sphere.
\[\varphi (z)\,=\, - \int^{z}_{\infty} E \mathrm{d}z \]We substitute the intensity size, expressed in section Intensity Outside The Sphere
\[E \,=\, \frac{\varrho R^3}{3 \varepsilon_0}\,\frac{1}{z^2}\], into the integral and factor out all constants from the integral:
\[\varphi (z)\,=\, - \int^{z}_{\infty} \frac{\varrho R^3}{3 \varepsilon_0}\,\frac{1}{z^2} \,\mathrm{d}z \,=\, - \,\frac{\varrho R^3}{3 \varepsilon_0} \int^{z}_{\infty} \frac{1}{z^2}\, \mathrm{d}z\]We calculate the definite integral:
\[\varphi (z)\,=\,- \,\frac{\varrho R^3}{3 \varepsilon_0}\left[- \frac{1}{z}\right]^z_{\infty}\,.\]We substitute the limits of the integral and we obtain the value of potential outside the sphere at distance z:
\[\varphi (z)\,=\,\frac{\varrho R^3}{3 \varepsilon_0}\frac{1}{z}\]Note: If we want to express the potential using total charge Q, we will utilize the following relation: \(Q\,=\,\frac{4}{3}\pi R^3 \varrho\).
The following relation will then apply for potential outside the sphere:
\[\varphi (z)\,=\, \frac{Q}{4 \pi \epsilon_0} \, \frac{1}{z}\,.\]Solution: Potential Inside Charged Sphere
We will calculate the potential inside the sphere in the same manner as in the previous section. We will express the potential from the following relation:
\[ \varphi (z)\,=\, - \int^{z}_{\infty} \vec{E} \cdot \mathrm{d}\vec{z}\,=\, - \int^{z}_{\infty} E \mathrm{d}z \]We have to be wary of the electric intensity size since the intensity cannot be express by one relation throughout the integration path. The border where the expression changes is the surface of the sphere. Therefore we need to separate the integral into two part. First we have to bring the charge from the infinity to the surface of the sphere (that is to distance R from the centre of the sphere) and then from the surface to the inside of the sphere.
\[\varphi (z)\,=\, - \int^{R}_{\infty} E_v \mathrm{d}z - \int^{z}_{R} E_u \mathrm{d}z \]We will substitute the size of intensities that we have expressed in the previous sections:
\[E_v \,=\, \frac{\varrho R^3}{3 \varepsilon_0\,z^2}\] \[E_u \,=\, \frac{ \varrho}{3 \varepsilon_0\,}z\]and we will obtain:
\[\varphi (z)\,=\, - \int^{R}_{\infty} \frac{\varrho R^3}{3 \varepsilon_0\,z^2} \mathrm{d}z - \int^{z}_{R} \frac{ \varrho}{3 \varepsilon_0\,}z \mathrm{d}z \,.\]We factor out constants from integrals:
\[\varphi (z)\,=\, - \frac{\varrho R^3}{3 \varepsilon_0}\int^{R}_{\infty} \frac{1}{z^2} \mathrm{d}z - \frac{ \varrho}{3 \varepsilon_0\,}\int^{z}_{R} z \mathrm{d}z \]and we solve the integrals:
\[\varphi (z)\,=\,- \,\frac{\varrho R^3}{3 \varepsilon_0}\left[- \frac{1}{z}\right]^R_{\infty}- \,\frac{\varrho }{3 \varepsilon_0}\left[\frac{z^2}{2}\right]^z_{R}\] \[\varphi (z)\,=\,- \,\frac{\varrho R^3}{3 \varepsilon_0}\left(- \frac{1}{R}\right)- \,\frac{\varrho }{3 \varepsilon_0}\left(\frac{z^2}{2}-\frac{R^2}{2}\right)\]Note: We didn’t have to calculate the first integral. All we had to do was to substitute z = R into the result of the previous section.
We factor out \(\frac{\varrho}{3 \varepsilon_0}\) and adjust the equation.
\[\varphi (z)\,=\, \,\frac{\varrho}{3 \varepsilon_0}\left(R^2 - \,\frac{z^2}{2} + \frac{R^2}{2}\right)\] \[\varphi (z)\,=\, \,\frac{\varrho}{3 \varepsilon_0}\left(\frac{3R^2}{2} - \,\frac{z^2}{2} \right)\] \[\varphi (z)\,=\, \,\frac{\varrho R^2}{6 \varepsilon_0}\left(3 - \frac{z^2}{R^2} \right)\]We obtained the relation for potential calculation inside the charged sphere.
Note: If we wanted to express the potential using total charge Q, we would use relation \(Q\,=\,\frac{4}{3} \pi R^3 \varrho\) and we would obtain
\[\varphi (z)\,=\, \,\frac{Q}{8 \pi \varepsilon_0 R}\,\left(3 - \frac{z^2}{R^2} \right)\,.\]Answer
The electric field intensity has the following size outside the sphere:
\[E \,=\, \frac{1}{4 \pi \varepsilon_0}\,\frac{Q}{z^2} \,=\, \frac{\varrho R^3}{3 \varepsilon_0}\, \frac{1}{z^2} \,.\]The electric field intensity has the following size inside the sphere:
\[E\,=\,\frac{Q}{4 \pi \varepsilon_0 R^3}\,z \,=\, \frac{ \varrho}{3 \varepsilon_0\,}z\,.\]The vector of electric intensity point away from the centre of the field in both cases.
The electric potential has the following value outside the sphere:
\[\varphi (z)\,=\, \,\frac{Q}{4 \pi \varepsilon_0}\frac{1}{z}\,=\, \,\frac{\varrho R^3}{3 \varepsilon_0}\frac{1}{z}\,.\]The electric potential has the following value inside the sphere:
\[\varphi (z)\,=\, \,\frac{Q}{8 \pi \varepsilon_0 R}\left( 3- \frac{z^2}{R^2}\right)\,=\, \,\frac{\varrho R^2}{6 \varepsilon_0}\left(3 - \frac{z^2}{R^2}\right)\,.\]Graphs
The graph of the electric intensity size dependence on the distance from the centre of the sphere
The electric intensity has the following size inside the charged sphere \(E\,=\, \frac{ \varrho}{3 \varepsilon_0\,}z\,,\)
and the following outside the sphere: \(E \,=\, \frac{\varrho R^3}{3 \varepsilon_0}\, \frac{1}{z^2} \,.\)
The first part of the graph (for values z from 0 to R) make up a line that goes through the origin. The intensity decreases with the second power of z for z greater than R.
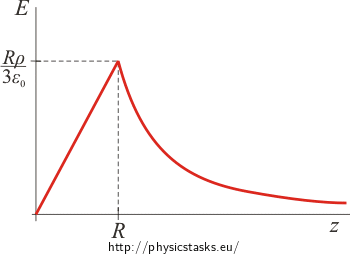
The graph of the function is continuous. We can prove that by substituting z = R into both expressions of the electric intensity. In both cases the electric intensity equals \(E(R)\,=\,\frac{R \varrho}{3 \varepsilon_0}\,.\)
Note: The intensity of the electric field is continuous except for points that lie outside the sphere’s surface. When going through the surface, the tangent component of the intensity remains continuous but the normal component „jumps“ according to the areal charge density.
The graph of the electric potential dependence on the distance from the centre of the sphere
The electric potential has the following value inside the sphere: \(\varphi (z)\,=\, \,\frac{\varrho R^2}{6 \varepsilon_0}\left(3 - \frac{z^2}{R^2}\right)\,,\)
and the following outside the sphere: \(\varphi (z)\,=\, \,\frac{\varrho R^3}{3 \varepsilon_0}\frac{1}{z}\,.\)
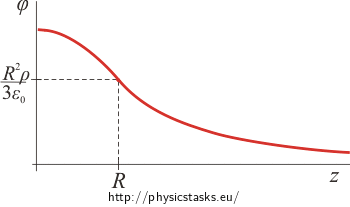
The function is continuous at point z = R again. If we substitute the value of z into both expressions, we obtain the same value: \(\varphi(R) \,=\,\frac{R^2 \varrho}{3 \varepsilon_0}\).
The function also has all first derivatives continuous at this point so it is smooth.
The electric potential is always continuous since it describes work when transporting a unit charge and the work cannot „jump“.
How to choose the Gauss area?
The easiest was of finding the electric intensity of an electric field (in the case of symmetric charge spread) is using the Gauss theorem:
\[\oint_S \vec{E} \cdot \mathrm{d}\vec{S}\,=\, \frac{Q}{\varepsilon_0}\]The Gauss theorem expresses the relation between the electric intensity flux through a closed area (the left hand side of the equation, the closed area is often called the Gauss area) and the total charge Q which lies inside this sphere.
The expression on the left hand side can also be expressed as:
\[\oint \vec{E} \cdot \vec{n}\,\mathrm{d}S\,=\, \frac{Q}{\varepsilon_0}\,,\]where \(\vec{n}\) is the outer normal unit vector of the area.
The most important step of solving a task using the Gauss theorem is the selection of the Gauss area. We try to choose it so that we can express the scalar product \(\vec{E} \cdot \vec{n}\) as easily as possible. We can distinguish three cases:
- The vector of the electric intensity is parallel to the Gauss area and therefore it is perpendicular to the normal vector. The scalar product is then zero and the flux through the area is zero.

The vector of the electric intensity is perpendicular to the Gauss area and therefore it is parallel with the normal vector and the flux is maximal. The scalar product is then equal to the product of sizes of both vectors \(| \vec{E} \cdot \vec{n}|\,=\,En\,=\,E\).

The vector of electric intensity has the same size in all points of the Gauss area in the sipliest case. The size of the intensity can then be factored out of the integral as a constant.
The vector of the electric intensity forms a different angle with the normal vector of the Gauss area and the flux is between zero and maximal. The scalar product is then equal to \(\vec{E} \cdot \vec{n}\,=\,En\cos\alpha\,=\,E\cos\alpha\).

This generic area isn’t too useful for calculations.
When choosing the Gauss area, we try to fit the first two cases as much as possible - that is to make individual parts of the sphere either perpendicular to or parallel with the vector of the electric intensity \(\vec{E}\) because it makes the calculation simple. The most common useful Gauss area is the surface of a cylinder or a sphere.
- The vector of the electric intensity is parallel to the Gauss area and therefore it is perpendicular to the normal vector. The scalar product is then zero and the flux through the area is zero.
Link to Similar Task
You can find out how the task changes should the charge inside the sphere be spread with non-constant density in task Unevenly Charged Ball.





