The motion of a charged particle in homogeneous perpendicular electric and magnetic fields
Task number: 402
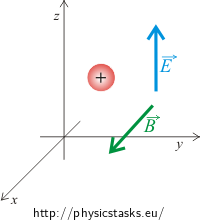
A particle with a positive charge Q begins at rest. Describe the motion of the particle after switching on both a homogeneous electric field with direction corresponding to the z axis and a homogeneous magnetic field with direction corresponding to the x axis.
Hint
There is a Lorentz force acting on a charged particle in an electromagnetic field. This force causes the particle’s movement. We should determine the particle’s trajectory, then find out an equation for the particle’s motion and solve it.
Analysis
A particle is placed in an electromagnetic field which is characterized by two vectors perpendicular to each other: electric field \(\vec{E}\) and magnetic field \(\vec{B}\). Both the electric and magnetic fields act on the particle with forces. The force of the electrical field is parallel to the electric field vector and also to the z axis. The magnetic force is perpendicular to the magnetic field vector which is parallel to the x axis. The net force of both the electric and magnetic forces acts in the yz plane. Because the particle’s initial velocity is zero, its motion will be in the yz plane.
Let’s find an equation for the charged particle’s motion and solve it.
Solution
There is no force acting on the particle in the direction of the x axis. The electrical force acts in the direction of the electric field, in our case it is the direction of the z axis. The magnetic force is perpendicular to the magnetic field which has the same direction as the x axis, so the magnetic force acts in the yz plane. Because the particle’s initial velocity is zero, its motion will be in the yz plane.
Let’s mark the particle’s position as:
\[\vec{r}(t)=\left(0,\,y(t),\,z(t)\right)\]We get the particle’s velocity by taking the time derivative of its position:
\[\vec{v}(t)=(0,\,v_y(t),\,v_z(t))=(0,\,\dot y(t),\,\dot z(t))\]The expression for the Lorentz force acting on a charged particle in an electromagnetic field is:
\[\vec{F}=Q\,(\vec{E}+\vec{v}\times\vec{B})\]The force \(\vec{F}\) could be also (according to Newton’s second law) expressed as the product of a particle’s mass and its acceleration:
\[\vec{F}=m\vec{a}=m \vec{\dot v}\]The equation of motion could now be rewritten as
\[m\vec{\dot v}=Q(\vec{E}+\vec{v}\times\vec{B})\]Let’s rewrite the electric field and magnetic field in terms of components:
\[\vec{E}=(0,\,0,\,E)\,\,\,\,\,\,\,\,\,\, \vec{B}=(B,\,0,\,0)\]Let’s find the vector product:
\[\vec{v}\,\times\,\vec{B}=(0,\,\dot y,\,\dot z)\,\times \,(B,\,0,\,0)=(0,\,B\dot z,\,-B\dot y)\]So, the equation of motion could be solved in three components as:
\[m\dot v_x=0\] \[m\dot v_y=0+QB v_z\] \[m\dot v_z=QE-QBv_y\]There is no force acting in the direction of the x axis and thus the particle’s velocity in the x direction is a constant (this ensues from the first equation). But we know that the constant must be zero, since the particle begins at rest. So as we assumed the motion will be only in the yz plane.
The second and third equation could resolved as
\[\dot v_y=\frac{QB}{m} v_z\tag{1}\] \[\dot v_z=\frac{QE}{m}-\frac{QB}{m}v_y\tag{2}\]We have obtained a system of two differential equations.
Let’s express the velocity vz from equation (1)
\[v_z= \frac{m}{QB}\dot v_y\]differentiate it with respect to time
\[\dot v_z= \frac{m}{QB}\ddot v_y\]and insert it into equation (2):
\[\frac{m}{QB}\ddot v_y=\frac{QE}{m}-\frac{QB}{m}v_y\]Multiplying both sides of the equation by the fraction \(\frac{QB}{m}\), we get:
\[\ddot v_y+\,\left(\frac{QB}{m}\right)^2v_y =\,\left(\frac{Q}{m}\,\right)^2EB\]We have now a non-homogeneous linear differential equation with constant coefficients. Its further solution can be found in the following section.
Solution of the differential equation
The equation
\[\ddot v_y+\,\left(\frac{QB}{m}\right)^2v_y =\,\left(\frac{Q}{m}\,\right)^2EB\tag{1}\]is a non-homogeneous linear differential equation with constant coefficients. Its solution has several steps.
First we have to solve the corresponding homogeneous equation, i.e. the equation with zero on its right side. Then we should find a particular solution, which is a random solution of the non-homogeneous equation. The general solution of a non-homogeneous equation is the sum of its particular solution and the general solution of the corresponding homogeneous equation. Constants in the general solution will be found from the initial conditions.
a) Solution of the homogeneous differential equation
\[\ddot v_h+\,\left(\frac{QB}{m}\right)^2v_h =0\]The solution has to be in the following form:
\[v_{h}(t)=e^{\alpha t}\] \[\ddot v_{h}(t)=\alpha^2e^{\alpha t}\]After substitution and some adjustment we get a new form of the equation
\[\alpha^2 e^{\alpha t}+\,\left(\frac{QB}{m}\right)^2e^{\alpha t}=0\] \[\alpha^2+\,\left(\frac{QB}{m}\right)^2=0\]which is a quadratic equation for an unknown α. Its solutions are
\[\alpha^2=-\,\left(\frac{QB}{m}\right)^2\] \[\alpha=\pm i\,\left(\frac{QB}{m}\right)\]To make it clearer let’s denote the fraction \(\frac{QB}{m}\) as
\[\Omega=\frac{QB}{m}\]The homogeneous equation then has two independent solutions
\[v_{h1}(t)=e^{i\Omega t}\] \[v_{h2}(t)=e^{-i\Omega t } \]A general solution is their linear combination
\[v_{h}(t)=Ae^{i\Omega t}+Be^{-i\Omega t}\tag{2}\]Let’s rewrite these complex exponentials using trigonometric functions
\[e^{i\Omega t}= \cos{(\Omega t)}+i\,\sin{(\Omega t)}\] \[e^{-i\Omega t}= \cos{(\Omega t)}-i\,\sin{(\Omega t)}\]and insert into equation (2).
\[v_{h}(t)=A[\cos{(\Omega t)}+i\,\sin{(\Omega t)}]+B[\cos{(\Omega t)}-i\,\sin{(\Omega t)}]\]After some rearranging we get
\[v_{h}(t)=(A+B)\cos{(\Omega t)}+i(A-B)\,\sin{(\Omega t)}\]Let’s mark the sum and the difference of constants A and B as two new constants C and D.
\[v_{h}(t)=C\,\cos{(\Omega t)}+\,D\,\sin{(\Omega t)}\]We have now got a general solution of the homogeneous equation, where C and D are real constants (because we are looking only for real solutions of the given differential equation).
b) Particular solution
The particular solution is one random solution of a non-homogenous differential equation, i.e. an equation with nonzero right side. There are various sorts of methods to do this, but in simple cases we can try to “guess” the solution. Actually, this often works very well.
In our case equation (1) has on its right side a constant. Let’s see if a particular solution of the non-homogenous equation vp could be a constant function.
\[v_{p}=\mathrm{konst}\]Derivations of such a particular solution are
\[\dot v_{p}=0\] \[\ddot v_{p}=0\]Let’s insert those expressions into equation (1)
\[\ddot v_{p}+\,\left(\frac{QB}{m}\right)^2v_{p} =\,\left(\frac{Q}{m}\,\right)^2EB\] \[0+\left(\frac{QB}{m}\right)^2v_{p} =\,\left(\frac{Q}{m}\,\right)^2EB\]Then express vp
\[v_{p}B =E\] \[v_{p} =\frac{E}{B}\]A particular solution has been found. It is the constant \(v_\textrm{p}=\frac{E}{B}\).
c) Complete solution of the non-homogeneous differential equation
We will get a general solution of a non-homogenous equation from the sum of its particular solution and the general solution of the relevant homogeneous equation, so
\[v_y=v_h+v_p\] \[v_{y}(t)=C\,\cos{(\Omega t)}+\,D\,\sin{(\Omega t)}+ \frac{E}{B}\tag{3}\]d) Determination of the constants C and D
The constants C and D can be determined from initial conditions. At the beginning (time t = 0 s) the particle was at rest so
\[v_y(0)=0\] \[v_{y}(0)=C\,\cos{0}+\,D\,\sin{0}+ \frac{E}{B}=0\] \[C+\,\frac{E}{B}=0\]We get the magnitude of the constant C
\[C=-\frac{E}{B}\]To determine the second constant D let’s find the component of the velocity vz. This component can be expressed as
\[v_z= \frac{m}{QB}\,\dot v_y\]The acceleration \(\dot v_y\) is determined by time differentiation of the expression for the velocity vy.
\[v_{y}(t)=C\,\cos{(\Omega t)}+\,D\,\sin{(\Omega t)}+ \frac{E}{B}\] \[\dot v_{y}(t)=-C\Omega\,\sin{(\Omega t)}+D\Omega\,\cos{(\Omega t)}\]The component of velocity vz is
\[v_z(t)= \frac{m\Omega}{QB}\,\left(-C\,\sin{(\Omega t)}+D\,\cos{(\Omega t)}\right)\tag{4}\]From the initial conditions vz(0) = 0 we may get the constant D
\[v_z(0)= \frac{m\Omega}{QB}\,D=0\] \[D=0\]Insert the determined constants C and D into the general solution (3)
\[v_{y}(t)=C\,\cos{(\Omega t)}+\,D\,\sin{(\Omega t)}+ \frac{E}{B}=-\frac{E}{B}\,\cos{(\Omega t)}+ \frac{E}{B}\]The component of velocity vy in the direction of the y axis is
\[v_{y}(t)=\frac{E}{B}(1-\,\cos{(\Omega t)}).\]The component of velocity vz we may determine from equation (4) by inserting constants C and D
\[v_z(t)= \frac{m\Omega}{QB}\,\left(-C\,\sin{(\Omega t)}+D\,\cos{(\Omega t)}\right)\] \[v_z(t)= \frac{m\Omega}{QB}\,\left(\frac{E}{B}\,\sin{(\Omega t)}\right).\]Be aware that
\[\Omega=\frac{QB}{m},\]and then for the z component of velocity we get
\[v_z(t)= \frac{E}{B}\,\sin(\Omega t).\]Solution - looking for a trajectory
By solution of the differential equation we have got the component of velocity vy
\[v_{y}(t)=\frac{E}{B}(1-\,\cos{(\Omega t)})\]And the component of velocity vz
\[v_z(t)=\frac{E}{B}\,\sin{(\Omega t)},\]where\(\,\,\,\Omega=\frac{QB}{m}\)
The components of position y and z we obtain by integration over time of the respective components of velocity.
\[y=\int{v_y}\,dt=\int{\frac{E}{B}\,\left(1-\,\cos{(\Omega t)}\right)}\,\mathrm{d}t\] \[y=\frac{E}{B\Omega}\,\left(\Omega t-\sin{(\Omega t)}\right)+y_0\]The component z can be determined by
\[z=\int{v_z}\,\mathrm{d}t=\int{\frac{E}{B}\,\sin{(\Omega t)}}\,\mathrm{d}t\] \[z=-\frac{E}{B\Omega}\,\cos{(\Omega t)}+z_0\]Integration constants \(y_0\) and \(z_0\) can be calculated from the initial conditions. Let us assume that at the time \(t=0 \mathrm{s}\) is the particle located in the origin of the coordinate system. Then:
\[ 0=y\left(0\right)=\frac{E}{B\Omega}\,\left(\Omega \cdot 0-\sin{\left(\Omega \cdot 0 \right)}\right)+y_0 \] \[ 0=z\left(0\right)=-\frac{E}{B\Omega}\,\cos{\left(\Omega \cdot 0\right)}+z_0 \] \[ y_0=0 \] \[ z_0=\frac{E}{B \Omega}. \]The trajectory of a charged particle in a homogeneous electromagnetic field is thus described by the following equations
\[x=0,\] \[y=\frac{E}{B\Omega}\,\left(\Omega t-\sin(\Omega t)\right),\] \[z=\frac{E}{B\Omega}\left(1-\cos(\Omega t)\right),\]where \(\Omega=\frac{QB}{m}\).
The shape of the trajectory
The equations describing the trajectory of a particle in a homogeneous electromagnetic field are
\[x=0,\] \[y=\frac{E}{B\Omega}\,\left(\Omega t-\sin(\Omega t)\right),\] \[z=\frac{E}{B\Omega}\left(1-\cos(\Omega t)\right),\hspace{15px}\Omega=\frac{QB}{m}.\]The motion of the trajectory is composed of two independent motions – one is circular motion in the plane yz with radius \(\frac{E}{B\Omega}\) and the other is uniform motion in the y. Combining those motions leads to motion on a cycloid (a cycloid curve).
\[x=0\] \[y=a(T-\sin{T})\] \[z=a(1-\cos{T})\]where a is the radius of the circle and T is the angle made by the rolling of the circle (see below).
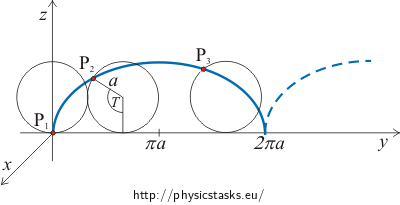
Remark: The motion of a particle in a uniform electromagnetic field could be compared to the motion of the tire valve of a moving wheel. Both of these motions have a cycloid trajectory.
Answer
After switching on both an electric field in the z direction and a homogeneous magnetic field in the x direction, the charged particle will move on a cycloid given by the equations
\[x=0,\] \[y=\frac{E}{B\Omega}\,\left(t\Omega-\sin(\Omega t)\right),\] \[z=\frac{E}{B\Omega}\left(1-\cos(\Omega t)\right),\,\,\,\,\,\,\,\,\,\,\,\Omega=\frac{QB}{m}.\]



