Consumption of Car Light Bulbs
Task number: 1791
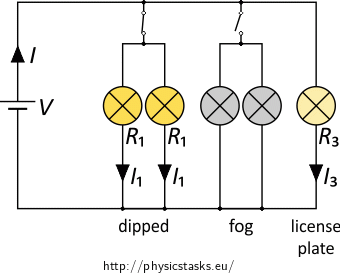
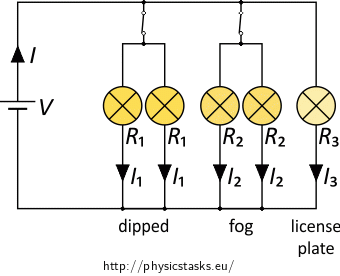
A car battery with a voltage of \(12\,\mathrm{V}\) powers the lightbulbs of: two dipped headlights, each with a resistance \(R_1 = 2{.}5\,\mathrm{\Omega}\); two fog lights, each with a resistance \(R_2=4\,\mathrm{\Omega}\) and one lightbulb the license plate lighting with a resistance \(R_3=30\,\mathrm{\Omega}\). All the bulbs are connected in parallel.
Determine the total resistance and the drawn current when there is the license plate lighting turned on together with:
Calculate the currents drawn by each bulb in both cases.
The light bulb resistances are given while hot. Neglect the current drawn by other elements.
Theory
We need Ohm’s law for a segment of an electric circuit:
\[ V = RI, \]where \(V\) is the voltage across a piece of conductor that has the resistance \(R\), and a current \(I\) flows through it.
If there are resistors (such as light bulbs) connected in series, their resistances sum up
\[ R_\mathrm{total} = R_1 + R_2 + \ldots + R_n, \]if they are connected in parallel, the reciprocals of the resistances sum up to the reciprocal of the total resistance
\[ \frac{1}{R_\mathrm{total}} = \frac{1}{R_1} + \frac{1}{R_2} + \ldots + \frac{1}{R_n}, \] Considering the very low internal resistance of the car battery and the relatively low consumption of the light bulbs (compared to starting currents), we assume that the battery is an ideal source in this case, i.e. \(U \neq U(I)\).a) Hint – dipped headlights
Draw the circuit diagram for the case when the dipped headlights are turned on. The bulbs are connected in parallel. How do we calculate the total resistance of such circuit?
Calculate also the total current and the current through each light bulb.
b) Hint – Switching on the fog lights
Draw the circuit diagram for the case when the fog lights are turned on in addition to the previous case. The bulbs are connected in parallel again. How do we calculate the total resistance of the circuit?
Calculate also the total current and the current through respective light bulbs.
Answer
The total resistance of the circuit is \(1{.}2\,\mathrm{\Omega}\) when only the dipped lights with the license plate lighting are turned on. The resistance of the circuit decreases to \(0{.}75\,\mathrm{\Omega}\) when we turn on the fog lights in addition.
The current drawn by the lighting circuit increases from \(10\,\mathrm{A}\) to \(16\,\mathrm{A}\) after turning on the fog lights.
One dipped light bulb draws a current of \(4{.}8\,\mathrm{A}\), the fog light bulb draws \(3\,\mathrm{A}\) and the license plate light bulb draws \(0{.}4\,\mathrm{A}\).