Collection of Solved Problems in Physics

Current-carrying wire in a magnetic field

Task number: 287

A wire having a length of 5 cm and a weight of 50 g is hanged on two thin conductors. If the wire carries a current of 10 A it deflects from the verticle in homogenous magnetic field by an angle of 14°. Derive the expression for the magnetic field.

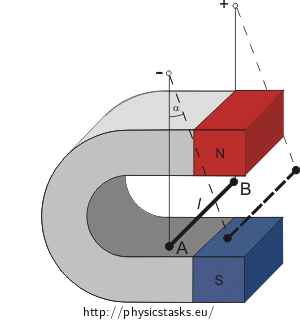
• Hint

  Think about the forces acting on the current-carrying wire in magnetic field. Draw them into a picture (the free body diagram) and determine the net force (their resultant force).

• Analysis

  First of all we have to realize which forces are acting on the current-carrying wire. Since the wire in placed in a magnetic field it is a magnetic force. Its direction, given by the left-hand rule, points to right. Next, there is the weight acting on the wire downwards. The sum of these forces gives the final force acting on the wire (see picture) which compensates the forces of the two thin conductors on which the wire is hanged. Hence this sum must point in the direction of deflected conductors.

  Using the triangle with an angle α and the tangent function we can derive the relation between the magnetic force and the weight and from it we can obtain the size of the magnetic force.

  Finally we can deduce the magnetic induction from the size of the magnetic force.

  (Fleming’s) left-hand rule

  First you orient your left hand so that the outstretched fingers point in the direction of the current and the magnetic field lines enter into your palm. If your hand is oriented in this way, then the extended thumb points in the direction of the magnetic force on the wire.

  

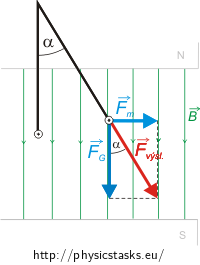
• Solution

  There are two forces acting on the wire which we need to determine: the weight \(\vec{F}_G\) and magnetic force \(\vec{F}_m\).

  Using the triangle with an angle α and the tangent function we derive the relation between the magnitudes of these forces F_G a F_m.

  \[\mathrm{tg}\alpha=\frac{F_m}{F_G}\]

  We express the magnetic force F_m as

  \[F_m=F_G \mathrm{tg}\alpha\tag{1}\]

  The magnitude of the magnetic force F_m acting on a straight wire is proportional to the current I through the wire, to the length l of wire in the magnetic field, and to the magnetic field B

  \[F_m=BIlsin\beta,\]

  where β is the angle between the wire and the magnetic field. In our case (see picture)

  \[\beta=90^o\,\,\,\Rightarrow\,\,\,sin\beta =1\]

  We insert the force \(F_m\) into the expression (1)

  \[BIlsin\beta = F_G \mathrm{tg}\alpha\]

  From the previous expression we express the magnitude of magnetic field \(B\).

  \[B=\frac{F_G \mathrm{tg}\alpha}{Il}\]

  Finally we substitute the relation for the magnitude of the weight F_G = mg

  \[B=\frac{mg \mathrm{tg}\alpha}{Il}\]

• Numerical solution

  \[l\,=\,5\,\mathrm{cm}=\,0.05\,\mathrm{m}\] \[m\,=\,5\,\mathrm{g}=\,0.05\,\mathrm{kg}\] \[I\,=\,10\,\mathrm{A}\] \[\alpha\,=\,14^{o}\] \[g\,=\,10\,\mathrm{ms}^{-2}\] \[B\,=\,?\]

  ---

  \[B\,=\,\frac{mg\mathrm{tg}\alpha}{Il}\,=\,\frac{0.05{\cdot}10\cdot \mathrm{tg}14^{o}}{10{\cdot}0{,}05}\,\mathrm{T}\, \dot{=}\,0.25\,\mathrm{T}\]

• Answer

  The expression for the magnetic field reads:

  \[B=\frac{mgtg\alpha}{Il}\]

  For the given numerical values it makes:

  \[B\, \dot{=}\,0.25\,\mathrm{T}.\]