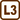Balanced Bridge
Task number: 2169
A bridge containing resistors R1, R2, R3 and a resistor R4 whose resistance is temperature dependent, is balanced. Calculate the temperature t of resistor R4.
At 0 °C (so-called reference temperature) resistor R4 has resistance of 4.5 kΩ, temperature coefficient of resistance equals 0.004 °C-1 and the values of the other resistors are R1 = 2.0 kΩ; R2 = 2.3 kΩ; R3 = 4.0 kΩ.
Hint 1
Recall or look up the meaning of “balanced bridge”.
Hint 2
How does one calculate the resistance of a temperature-dependent resistor?
Hint 3
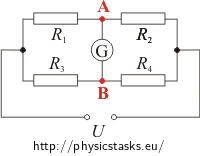
What voltage is there between points A and B if no current runs through the galvanometer? What does it imply about the electric potential of these points?
Analysis

If the bridge is balanced, then there is no current running through galvanometer G. These thus apply:
- Current running through resistor R1 will be equal to the current running through resistor R2 (the same applies to resistors R3 and R4).
- The voltage between points A and B is zero. Voltage between two points is equal to the difference of their potential, thus nodes A and B have the same electric potential. Therefore, voltages on resistors R1 and R3 are equal (same goes for R2 and R4).
Using Ohm’s law and these thoughts, we get a rule for a balanced bridge: the quotient of resistances of resistors R1 and R2 is equal to the quotient of resistances of resistors R3 and R4.
The resistance of resistor R4 is temperature-dependent. The resistance can be calculated using this relation:
\[R_4\,=\,R_0\left(1\,+\,\alpha \Delta t\right),\]where R is the resistor’s resistance at temperature t, R0 is the resistor’s resistance at initial (so-called reference) temperature t0, α is temperature coefficient of electric resistance and Δt is the temperature difference Δt = t0.
Solution

If the bridge is balanced, then no current runs through galvanometer G. Thus nodes A and B will have the same electric potential and:
1. Current running through resistor R1 is equal to current running through resistor R2. Current running through resistor R3 is equal to current running through resistor R4. Thus:
\[I_1\,=\,I_2\] \[I_3\,=\,I_4\]2. Voltages on resistors R1 and R3 are the same because nodes A and B have the same electric potential. The same applies to resistors R2 and R4.
\[U_1\,=\,U_3\] \[U_2\,=\,U_4\]Ohm’s law says:
\[U_x\,=\,R_xI_x,\]where Ux is the loss of voltage at an appliance, Rx is the resistance of the appliance and Ix is the current that runs through the appliance.
Now we will formulate equations for resistors:
\[R_1I_1\,=\,R_3I_3\] \[R_2I_2\,=\,R_4I_4.\]We divide both equations:
\[\frac{R_1I_1}{R_2I_1}\,=\,\frac{R_3I_3}{R_4I_3}.\]Currents I1 and I3 will be reduced in the fractions and we will receive the condition for a balanced bridge:
\[\frac{R_1}{R_2}\,=\,\frac{R_3}{R_4}.\]Now we express resistance R4 from the equation:
\[R_4\,=\,\frac{R_2R_3}{R_1}.\tag{*}\]The resistance of resistor R4 is temperature-dependent. This dependence is described by relation
\[R_4\,=\,R_0\left(1\,+\,\alpha \Delta t\right),\]where R is the resistor’s resistance at temperature t, R0 is the resistor’s resistance at initial (so-called reference) temperature t0, α is temperature coefficient of electric resistance and Δt is the temperature difference Δt = t0.
We will formulate from this equation the temperature difference Δt:
\[1\,+\,\alpha\Delta t\,=\,\frac{R_4}{R_0}\] \[\alpha\Delta t\,=\,\frac{R_4}{R_0}-1\,=\,\frac{R_4-R_0}{R_0}\] \[\Delta t\,=\,t-t_0\,=\,\frac{\frac{R_4-R_0}{R_0}}{\alpha}\,=\,\frac{R_4-R_0}{\alpha R_0}.\]For temperature t this applies:
\[t\,=\,\frac{R_4-R_0}{\alpha R_0}\,+\,t_0.\]Now we will substitute for R4 using relation (*):
\[t\,=\,\frac{\frac{R_2R_3}{R_1}-R_0}{\alpha R_0}\,+\,t_0,\]which will give us the relation for temperature t of resistor R4:
\[t\,=\,\frac{R_2R_3\,-\,R_0R_1}{\alpha R_0R_1}\,+\,t_0.\]List of known information and substitution
We know from the assignment:
R1 = 2,0 kΩ resistances of resistors R1, R2, R3 of the bridge R2 = 2,3 kΩ R3 = 4,0 kΩ R0 = 4,5 k Ω resistance of resistor R4 at temperature 0 °C α = 0,004 °C-1 temperature coefficient of electric resistance of resistor R4 t = ? (°C) temperature of resistor R4
Note: All resistances are given in kiloohms and the unit ohm cancels out, so we do not have to convert them.
\[ t\,=\,\frac{R_2R_3\,-\,R_0R_1}{\alpha R_0R_1}\,+\,t_0\,=\,\frac{2{,}3{\cdot} 4-4{,}5{\cdot} 2}{0{,}004{\cdot} 4{,}5{\cdot} 2}\,{}^\circ\mathrm{C}\,+\,0\,{}^\circ\mathrm{C}\,=\,5{,}5\,{}^\circ\mathrm{C}\]Answer
If the bridge is balanced, then the temperature of resistor R4 is 5.5 °C.
Other ways of solving this problem
Another possible, though more complicated, way of solving this problem is the usage of Kirchhoff’s laws. You can formulate the current running through the galvanometer under general conditions and then calculate when the current will be equal to zero.
Kirchhoff’s laws and a “cookbook“ of their usage can be found in Using Kirchhoff’s laws to solve circiut with two power supplies
Comment
Measuring bridges are used for measuring of electric capacity, resistance and inductance. Measuring with bridges is based on reaching balance between branches of the bridge. This balance is determined by galvanometer which is connected to one diagonal of the bridge. A current source is connected to the other, dc or ac depending on the measured quantity (ac for capacity and inductance, both ac and dc for resistance, dc being the better one).
Measuring with bridges is very precise but can be used only in a small range (depends on the bridge’s parameters).
Specially constructed devices are based on balanced bridges and are used for measuring electric resistances. They are called ohmmeters.