Dielectric lift
Task number: 658
Two long coaxial tubes (with inner radius a and outer radius b) are placed vertically into a container with oil (relative permittivity εr, density ρ). The inner tube has potential U, the second is grounded. What is the height h in which the oil between tubes ascends to?
Use this equation: cylindrical capacitor with length l with inner radius a and outer radius b filled by dielectric with relative permittivity εr has a capacity C
\[C = \frac{2\pi\varepsilon l}{\ln (b/a)}\]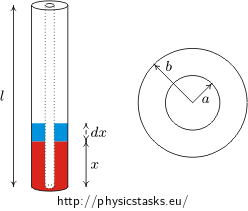
Hint 1
Oil is drawn into the capacitor by electric forces. Against them is gravitational force. Oil is drawn to such a height to these two forces.
Hint 2
Change of energy of capacitor is equals the work to rise a dielectric of height dx. The force is derivative of work with respect to position.
Calculate for that reason the change of capacity of the capacitor dC, if dielectric rises from height x to height x+dx.
Calculate the change of energy of the capacitor if capacity is changed of dC (by change of height of liquid of dx). Be aware of the fact that capacitor is connected to power supply which means that it has constant voltage between both electrodes.
Hint 3
To calculate the change of capacity of the capacitor determine first capacity of the capacitor when dielectric has part x of total length l of the cylindrical capacitor. Use the equation from the assignment and note that the capacitor is actually two capacitors in parallel (one filled by air, second by dielectric – oil).
After that replace x+dx with x in equation for capacity of capacitor and substract both of the equations from each other. Than you gain dependence of change of the capacity dC on small displacement of the surface of the liquid dx.
Analysis
Power source in which the cylindrical capacitor is connected can do some work. This work is used to rise the dielectric to space between tubes. The done work is manifested as rising of energy of the capacitor.
Forces which draw dielectric between the tubes have electrical character. The principle of their action is too complicated to calculate them directly from knowledge of electric field.
Instead of that we can take into consideration that force is derivative of work which is done to dielectric with respect of displacement. The work done is manifested as change of electric energy of the capacitor and we can calculate this change from known equations.
Strategy of solution of task is following: we calculate value dE in which the energy of the capacitor is changed during small displacement dx of dielectric in upwards direction. Energy dE is equal to work which is done by electric forces, so fraction dE/dx determines value of affecting electric forces.
If there were no effect of gravity, oil would fill ups all capacitor. But there is gravity force too and its direction is against the direction of electric forces. Oil rises to such a height to equal these two forces.
Solution
When l is total height of tubes then the tubes together with space between them which is filled partially with oil (to height x) and partially with air from a cylindrical capacitor with capacity
\[C = C_{oil} + C_{air} = 2\pi\varepsilon\,\frac{x}{\ln (b/a)}+ 2\pi\varepsilon_0\,\frac{l-x}{\ln (b/a)} =\] \[= 2\pi\varepsilon_0\,\frac{\varepsilon_r x}{\ln (b/a)} + 2\pi\varepsilon_0\,\frac{l-x}{\ln (b/a)} = 2\pi\varepsilon_0\,\frac{(\varepsilon_r-1)x+l}{\ln (b/a)}\ .\]The equation follows from the fact that there are actually two capacitors connected in a parallel (one with length x filled with oil and the second with length l-x filled with air).
When the surface of the oil in the capacitor rises in height dx then the capacity of capacitor changes of value
\[{\rm d}C = 2\pi\varepsilon_0\,\frac{(\varepsilon_r-1)(x+{\rm d}x)+l}{\ln (b/a)} - 2\pi\varepsilon_0\,\frac{(\varepsilon_r-1)x+l}{\ln (b/a)} = 2\pi\varepsilon_0\,\frac{(\varepsilon_r-1){\rm d}x}{\ln (b/a)}\]The energy of capacitor will modify as an impact of this change,
\[{\rm d}E = \frac{1}{2}U^2\,{\rm d}C\]which responds to the work done
\[{\rm d}E = {\rm d}W = F\,{\rm d}x\]which is caused by force F with effect on dielectric. We have now
\[F = \frac{{\rm d}W}{{\rm d}x} = \frac{{\rm d}E}{{\rm d}x} = \frac{1}{2}U^2\frac{{\rm d}C}{{\rm d}x} = \frac{1}{2}U^22\pi\varepsilon_0\frac{\varepsilon_r-1}{\ln (b/a)}\]We calculated the effect of electric forces on dielectric. These forces draw the dielectric inside the capacitor up to such a height which is limited by gravity force. Then it is valid that
\[F = F_G = mg = \varrho\pi(b^2-a^2)gh\]from which follows
\[h = \frac{\varepsilon_0(\varepsilon_r-1)U^2}{\varrho(b^2-a^2)g\ln (b/a)}\]Comment
Electric forces affecting dielectric are caused by inhomogeneity of electric field on the boundary which is difficult to calculate accurately but we can use the consideration with energy instead of that.
Answer
Oil rises to height
\[h = \frac{\varepsilon_0(\varepsilon_r-1)U^2}{\varrho(b^2-a^2)g\ln (b/a)}\]Link to similar task
You can find different solution in task Kondenzátor s olejem (only in Czech), in which there is a plate capacitor instead of the cylindrical capacitor.




