Electron moving in a uniform field

Task number: 299

An electron flies into a homogenous electric field against the direction of the line of force. The initial electron velocity/speed is 10 km s^-1. The electric field intensity is 20 V m^-1. Calculate the speed/velocity of the electron when is has already moved/traveled 9 cm in the field.

Comment: This task can be solved by two different ways:

I. analysing electron movement

II. using the law of conservation of energy

I. Hint 1
What force (think about it’s size) affects the electron? What is the direction of that force?

What kind of movement does the electron undergo?
Picture
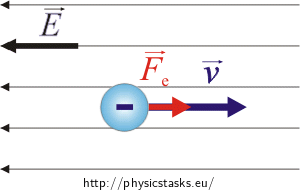
I. Hint 2
Accelerattion of the electron can be figured out by applying Newton’s second law of motion.
I. Analysis
A moving electron is affected by an electrical force proportional to the homogenous field intensity. The charge of an electron is negative, therefore the affecting force has the opposite direction in comparation with the electric field vector. So the force will be accelerating the electron.

To evaluate the velocity of the electron, we can use the uniformly accelerated motion trajectory length formula (we have to not forget initial velocity). The acceleration can be evaluated using Newton’s second law and the time can be evaluated using the uniformly accelerated motion velocity formula.
I. Solution: Electron
The electron is affected by the force, which size is given by
\[F_e\,=\,eE\,.\tag{1}\]
Electron charge is negative therefore the direction of the force affecting the electron is oposite to the direction of the electric intensity field \(\vec{E}\). So the force will uniformly accelerate the electron. Using Newton’s second law of motion we can evaluate the acceleration a:
\[a\,=\,\frac{F_e}{m}\]
The electric force can be substituted from formula (1)
\[a\,=\,\frac{eE}{m}\,.\tag{2}\]
The electron moves with uniform acceleration, so its velocity is
\[v\,=\,at+v_0\]
(v₀ is the initial velocity of the electron)

We can evaluate the time t from that equation.
\[t\,=\,\frac{v-v_0}{a}\tag{3}\]
The lenght of the trajectory of uniformly accelerated movement is
\[s\,=\,\frac{1}{2}at^2+v_0t\]
Now we can use the evaluation of time from (3):
\[s\,=\,\frac{1}{2}a\left( \frac{v-v_0}{a}\right)^2+v_0\frac{v-v_0}{a}\]
And evaluate the velocity v from this formula.
\[s\,=\,\frac{1}{2} \frac{\left( v-v_0\right)^2}{a}+\frac{v_0\left(v-v_0\right)}{a} \hspace{20px}|\,\cdot 2a\] \[2sa\,=\,\left( v-v_0\right)^2 + 2v_0\left( v-v_0\right)\] \[2sa\,=\,v^2 - 2v_0v + v_0^2 + 2v_0v - 2v_0^2\] \[2sa\,=\,v^2 - v_0^2\hspace{20px}|\, +v_0^2\] \[ v^2\,=\,2sa+v_0^2\] \[v\,=\, \sqrt {2sa+v_0^2}\]
Now we can substitute the acceleration a from formula (1) to obtain the electron’s final velocity.
\[v\,=\,\sqrt {\frac{2seE}{m}+v_0^2}\]
II. Hint
How is the electron’s energy changing when the electron is moving in the homogenous field? Why does the change happen?
II. Analysis
Let’s use the conservation of energy law to calculate electron’s velocity.

The electron is affected by the electric force. It accelerates the electron and so the electron’s kinetic energy is increasing.

Note: The work done by the electric force is equal to the change in the potential energy.
II. Solution: Energy of the electron
When the electron moves the conservation of energy law is respected.
\[E_{k2}\,=\,E_{k1}+W_e\tag{*}\]
The electron’s kinetic energy can be evaluated from the formulas
\[E_{k1}\,=\,\frac{1}{2}m v_0^2\hspace{40px} E_{k2}\,=\,\frac{1}{2}m v^2,\]
where v₀ is the electron’s initial velocity.

W_e is the work, which has to be done by the electric force to accelerate the electron. The force is constant, so we can evaluate the work from the formula:
\[W_e\,=\,F_e s\]
The electric force is directly proportional to the charge of the electron e and also directly proportional to the electric field intensity E: \(F_e=eE\), so the work done by electric force is:
\[W_e\,=\,e E s\]
Now we can substitute the work and the kinetic energies into the conservation of energy law (*) to obtain the velocity v.
\[\frac{1}{2}m v^2\,=\,\frac{1}{2}m v_0^2 + e E s \hspace{20px}| \,\cdot \frac{2}{m}\] \[v^2\,=\,v_0^2 + \frac{2seE}{m}\] \[v\,=\,\sqrt {\frac{2seE}{m}+v_0^2}\]
Calculation
\[v_0\,=\,10\,\mathrm{km\,s}=10^4\,\mathrm{m\,s^{-1}}\] \[E\,=\,20\,\mathrm{V\,m^{-1}}\] \[s\,=\,9\,\mathrm{cm}\,=\,9{\cdot} 10^{-2}\,\mathrm{m}\] \[v\,=\,?\,\left(\mathrm{m\,s^{-1}}\right)\]
From mathematical and physical tables:
\[e\,=\,1.6 {\cdot} 10^{-19}\,\mathrm{C}\] \[m\,=\,9.1 {\cdot} 10^{-31}\,\mathrm{kg}\]
\[v\,=\,\sqrt {\frac{2seE}{m}+v_0^2}\] \[v\,=\,\sqrt {\frac{2\,\cdot\, 9{\cdot} 10^{-2} \,\cdot\, 1.6 {\cdot} 10^{-19}\,\cdot\, 20}{9.1 {\cdot} 10^{-31}}\,+\,\left(10^4\right)^2}\,\mathrm{m\,s^{-1}}\] \[v \,\dot=\, 800\,\mathrm{km\,s^{-1}}\]
Note: Although the electric field is quite weak, the electron is accelerated over a short distance to a quite high velocity. The reason is the electron weight is very small, so olny a small amount of energy is needed to accelerate it significantly.
Answer
In 9 cm of movement the electron’s velocity will increase to \[v\,=\,\sqrt {\frac{2seE}{m}+v_0^2}\,\,\dot=\,\,800\,\mathrm{km\,s^{-1}}\] .
What would change if....
What would change, if the electron moves inside the same homogenous electric field in the direction the field?

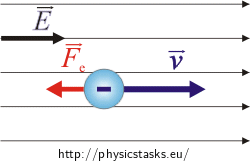
In this case the electric force direction is opposite to the direction of the electron’s velocity, so the electron would decelerate uniformly.