Collection of Solved Problems in Physics

Non-traditional circuits I.

Task number: 2338

What is the total electrical resistance of the following circuits if all the resistors have the same resistance R?

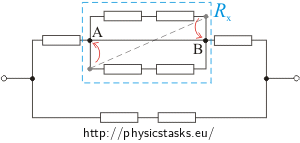
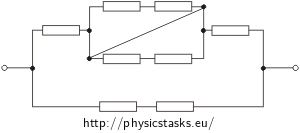
a)

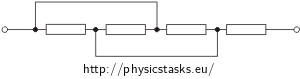
b)

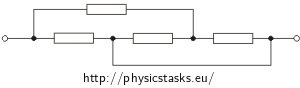
c)

• Hint 1

  The key to a successful solving of the problem is to draw the circuit in a more familiar and common way so that it is clear if it is in series or parallel.

• Hint 2

  "Bending" of wires during drawing the networks does not change any properties of network neither total resistance of the network.

• Breakdown

  During computation of total resistance it is necessary to have uncluttered schematic of the circuit. There are no general instructions for making the schematic. However, there are two tricks you can often use.

  1. If a wire connects two knots and there is no appliance on that wire we can merge these knots into one. For example, the following two pictures show the same wiring of the schematic a:

  

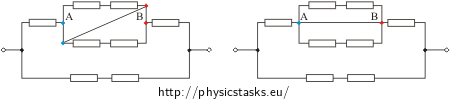
  2. In the second picture we are dealing with the following problem: we have parts of the circuit in parallel and one of the parallel branches is not laden by any appliance therefore there is no resistance (this part is a short circuit). All of the current between knots A and B will be flowing through this branch. There will be no current flowing through the other two branches therefore they do not affect the total resistance of the parallel part – resistance of the parallel part is zero (Note: we would come to this statement anyway if we merged the knots A and B).

  We will be solving the rest of the circuits using similar ideas.

  During computation of the total resistance we will use the following rules:

  1. For combinations of resistors in series the total resistance is equal to the sum of resistances of each resistor.
  2. For combinations of resistors in parallel the reciprocal value of total resistance is equal to sum of reciprocal values of resistance of each resistor.

• Solution of part a)

  We will draw the circuit in different way according to following ideas:

  Knots of wire which make the diagonal in the parallel part of the circuit R_x can be merged with knots A, B of the same parallel part (knots are on the same wire and there is no appliance in between them).

  

  Now we will look closer at the parallel part of the circuit marked R_x. It is obvious from the picture that this part consists of three parallel branches. One of them is not laden by any resistor therefore the whole current is flowing through this branch which comes to the knot. No current is flowing through the other two branches (they are "short-circuited") and they don’t affect the total resistance of part R_x.

  \[R_x\,=\,0\,\mathrm{\Omega}\]

  If part R_x has zero resistance the total resistance will depend on the two parallel branches where on every branch there are two resistors in series. These equations are for the two branches:

  \[R_u\,=\,R+R\,=\,2R\tag{upper branch}\] \[R_l\,=\,R_u\,=\,2R\,.\tag{lower branch}\]

  And for total resistance of this scheme:

  \[\frac{1}{R_\mathrm{total}}\,=\,\frac{1}{R_u}+\frac{1}{R_l}\,=\,\frac{1}{2R}+\frac{1}{2R}\,=\,\frac{2}{2R}\,=\,\frac{1}{R}\] \[R_\mathrm{total}\,=\,R\,.\]

• Dynamical element – redrawing of the circuit a)

  Following applet shows an animation of redrawing the circuit.

• Solution of part b)

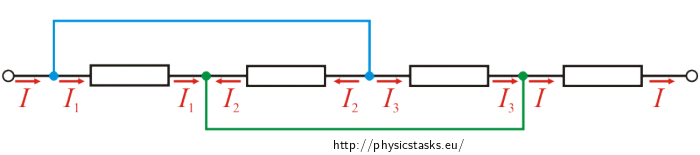
  As in the previous solution we can also merge some knots here (they are marked by colours in the following image). We will add the currents entering and leaving each knot to the picture.

  

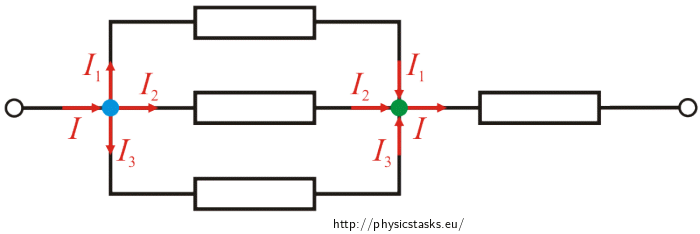
  Now we will redraw the schematic once again. We can see that the current I is being divided in three parts I₁, I₂, I₃. They will merge after all. So:

  

  Now we can compute the total resistance of the circuit as a sum of the resistance of resistor R and the resistance of the parallel part.

  For resistance of parallel part R_p we can write:

  \[\frac{1}{R_p}\,=\,\frac{1}{R}+\frac{1}{R}+\frac{1}{R}\,=\,\frac{3}{R}\] \[R_p\,=\,\frac{R}{3}\,.\]

  The total resistance of the circuit is:

  \[R_\mathrm{total}\,=\,R_p\,+\,R\,=\,\frac{R}{3}\,+\,R\] \[R_\mathrm{total}\,=\,\frac{4R}{3}\,.\]

• Dynamical element – redrawing of circuit b)

  Following applet shows an animation of redrawing the circuit.

• Solution of part c)

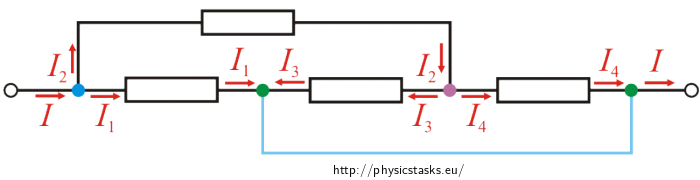
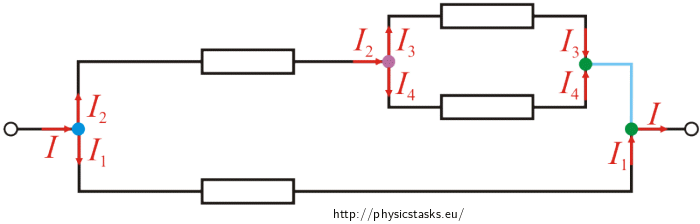
  We will mark the knots in different colours for this circuit as well. Only the knots which are connected by a branch (in picture marked as blue) with no resistor we will mark with same colour. These two knots are basically the "same" knots and we could merge them into one.

  

  Now we will redraw the circuit once again. In the picture we can see that in the blue knot the current I is divided into two currents I₁ and I₂. Current I₂ is further divided into two other currents I₃ and I₄.

  

  Now we will compute the total resistance of the circuit. Let us remind that all the resistors in the circuit have resistance R.

  In the upper branch of the schematic there are three resistors. Two are in parallel and the third is in series with them. For total resistance R_p of two resistors in parallel we can write:

  \[ \frac{1}{R_p}\,=\,\frac{1}{R}\,+\,\frac{1}{R}\,=\,\frac{2}{R} \] \[ R_p\,=\,\frac{R}{2}\,. \]

  Total resistance R_u for upper branch of integration is equal to the sum of resistances of one resistor and resistors in parallel part

  \[ R_u\,=\,R\,+\,R_p\,=\,R\,+\,\frac{R}{2} \] \[ R_u\,=\,\frac{3R}{2}\,. \tag{upper branch}\]

  Lower branch has just one resistor on it. Its resistance is therefore equal to the resistance of this resistor.

  \[ R_l\,=\,R\,. \tag{lower branch}\]

  Total resistance of the circuit is:

  \[ \frac{1}{R_\mathrm{total}}\,=\,\frac{1}{R_u}\,+\,\frac{1}{R_l}\,=\,\frac{2}{3R}\,+\,\frac{1}{R}\,=\,\frac{5}{3R} \] \[ R_\mathrm{total}\,=\,\frac{3R}{5}\, \]

• Dynamical element - redrawing of circuit c)

  Following applet shows an animation of redrawing the circuit.

• Answer

  Total resistances of individual circuits are: a) \(R\), b) \(\frac{4R}{3}\), c) \(\frac{3R}{5}\).

• Link to a similar task

  In exercise Non-traditional circuits II. try to compute the total resistance of three circuits.