Magnetic flux through a square
Task number: 552
Find the magnetic flux Φ through a square with side of 3 cm, which is located near a long straight conductor with electric current of 15 A. One side of the square is parallel to the conductor with distance of 4 cm between the side and the conductor. The opposite side of the square is located 5 cm away from the conductor.
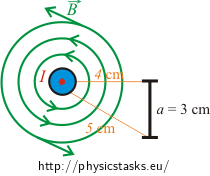
Hint
Notify the equation for the magnetic flux through a surface of a conductor loop. Because of the position of the square and the conductor, the value of the magnetic flux will not be a constant in the square area, it will differ with the position.
Analysis
First of all, we will write down the equation for the magnetic flux Φ. There is a magnetic flux density included in this equation which can be represented as a magnetic flux density for a long straight conductor in this case.
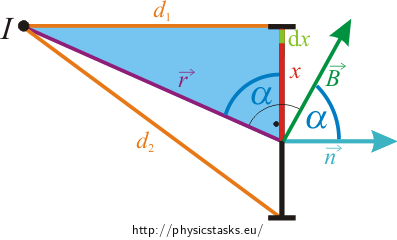
The distance of the conductor and the place, where we find the magnetic flux, will change with the position of the square. This distance is labeled as unknown r, which will be used as integral unknown.
The equation for the magnetic flux is integrated over the square area S. Let’s divide the square into smaller pieces with the same magnetic flux density. These pieces can be represented as narrow rectangles with sizes of a (which is parallel to the conductor) and dx (perpendicular to the conductor). We can express the size dx using the distance r (see the triangle in the image).
We express other unknowns in the equation for the magnetic flux using only the distance r.
Picture
Solution
The equation for the magnetic flux Φ through surface S has a form of
\[\Phi=\int_S{B\,\cos \alpha}\, \mathrm{d}S\]The magnetic induction B can be expressed as the magnetic induction near the long straight conductor in a following form:
\[B=\frac{\mu_0}{2\pi}\, \frac {I}{r}\]where r is a distance between the conductor and the place, where we find the size of the magnetic induction.
Because the distance r depends on the position in the square, we use it as integration unknown and express all other quantities in the magnetic flux equation using this unknown.
Element of area dS will be expressed as
\[\mathrm{d}S = a\, \mathrm{d}x\]where a is a side of the square parallel to the conductor and dx is an element part of the side perpendicular to the conductor, which should be expressed using integration unknown r.
Side x of the blue triangle in the picture can be expressed using Pythagorean theorem as:
\[ x=\sqrt{r^{2}-d_1^{2}} \]After derivation of this equation we get
\[ \mathrm{d}x=\frac{r}{\sqrt{r^{2}-d_1^{2}}}\,\mathrm{d}r \]We install this form into the equation for the element of area dS
\[ \mathrm{d}S=\frac{ar}{\sqrt{r^{2}-d_1^{2}}}\,\mathrm{d}r \]Now, we express the quantity cos α. Angle α is an angle between the direction of magnetic induction B and the perpendicular to the area. As we can see in the picture, the same angle is between the distance r and side x of the square. We express cos α using goniometric functions as
\[ \cos \alpha = \frac {x}{r}\]After installing for the x we get
\[ \cos \alpha = \frac {\sqrt{r^{2}-d_1^{2}}}{r}\]Now we have all parts of the equation for magnetic flux Φ expressed using one unknown r. We can install all these parts into the equation
\[ \Phi=\int_S{B\,\cos \alpha}\, \mathrm{d}S\] \[\Phi = \int_{d_1}^{d_2}{\frac{\mu_0 I}{2\pi r}\,\frac {\sqrt{r^{2}-d_1^{2}}}{r}\,\frac{ar}{\sqrt{r^{2}-d_1^{2}}}}\,\mathrm{d}r \]Integration will be done over interval from d1 to d2, where the distance r differs.
\[\Phi = \frac{a \mu_0 I}{2\pi} \int _{d_1}^{d_2}{\frac{1}{r}}\,dr = \frac{a \mu_0 I}{2\pi}ln\,\frac{d_2}{d_1}\]Comment – checking of expressing dS
Let’s check if we have expressed the equation for element of area dScorectly. The size of the square is a = 3cm. The area of square is S = a2 = 9 cm2.
The element of area dS was expressed as
\[ \mathrm{d}S=\frac{ar}{\sqrt{r^{2}-d_1^{2}}} \mathrm{d}r\]Integrating this equation over interval from d1 to d2 should give us the same area.
\[ S = \int_{d_1}^{d_2} {\frac{ar}{\sqrt{r^{2}-d_1^{2}}}}\, \mathrm{d}r\]Let’s solve the integral by substitution
\[l = r^2 - d_1^{2}\] \[ \mathrm{d}l = 2r\, \mathrm{d}r\] \[ \mathrm{d}r = \frac{ \mathrm{d}l}{2r}\]After installing and changing the interval bounds, we get:
\[S = \int_0^{d_2^{2}-d_1^{2}}{\frac{a}{2}}\,\frac{1}{\sqrt{l}}\, \mathrm{d}l =\frac{a}{2}\left[2\sqrt{l}\right]_0^{d_2^{2}-d_1^{2}} =\frac{a}{2}\left(2\sqrt{d_2^{2}-d_1^{2}}-2\sqrt{0}\right)\]After installing numbers we get:
\[S=\frac{3}{2}\left(2\sqrt{5^{2}-4^{2}}-2\sqrt{0}\right)\,\mathrm{cm^{2}}= 9\,\mathrm{cm^{2}}\]We can see that using the expression of the element of the aread S we got the correct area of the square.
Installing numbers
\[a = 3\,\mathrm{cm} = 0.03\,\mathrm{m}\] \[I = 15\,\mathrm{A}\] \[d_1=4\,\mathrm{cm}= 0.04\,\mathrm{m}\] \[d_2=5\,\mathrm{cm}= 0.05\,\mathrm{m}\] \[\Phi = ?\]
\[\Phi = \frac{a\mu_o I}{2\pi}ln\,\frac{d_2}{d_1} = \frac{0.03{\cdot} 4\cdot \pi \cdot 10^{-7}\cdot 15}{2\pi}\, ln \frac{5}{4}\,\mathrm{nWb}\, \dot{=} \,20 \,\mathrm{nWb}\]Answer
Magnetic flux Φ through a conductor square has value of approximately 20 nWb.



