Connecting Capacitors 1
Task number: 2321
Capacitors are connected as shown in the picture. Determine the total capacity of the circuit, the voltage and charge on plates of the capacitors when connected to voltage of 100 V.
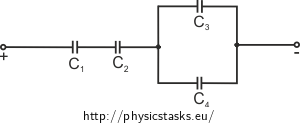
Calculate for general values and then for values \(C_1 = C_3 = 1\ µ\mathrm{F},\ C_2 = C_4 = 10\ µ \mathrm{F}\).
Note: You might be more familiar with capacity instead of capacitance.
Hint – Capacitance, Voltage and Charge
Capacitance expresses the ability of a conductor to keep electric charge. It is constant for a given capacitor (wire) and it is defined as
\[C = \frac {Q}{U},\]where Q is the charge on the capacitor with voltage of U.
Search for relations that relate to capacitance, voltage and charge for capacitors that are in series or parallel.
Analysis
We can replace parallel capacitors with a single capacitor with capacitance equal to the sum of capacitances of replaced capacitors. By doing this, we obtain a circuit with three serial capacitors. In this circuit, the inverse value of the total capacitance is equal to the sum of inverse values of all capacitors in the circuit. We will determine the total capacitance this way.
The total charge is directly proportional to the total capacitance and the total voltage (that is the source voltage).
If we know the voltage and the total capacitance of the circuit, we can calculate the total charge. The charges on capacitors 1, 2 and 34 are equal to the total charge. We can calculate the voltage from knowing the charge and the capacitance of the capacitor. The voltage on capacitors 3 and 4 is equal to the voltage on capacitor 34, we can calculate the charge from knowing the capacitance and voltage.

Solution – capacitance

We will utilize pieces of information from the hint for the total capacitance calculation. We will first take a look at the parallel part of the circuit and capacitors \( C_3,\ C_4\) will be replaced with capacitor \(C_{34} \) (accodring to the equation from the hint).
\[C_{34} = C_3 + C_4,\] \[C_{34} = 1\ µF + 10\ µF = 11 \ µF.\]
We will conduct the calculation analogically in the serial part of the circuit. Capacitors \( C_1,\ C_2, \ C_{34}\) will be replaced by a single capacitor \(C_\mathrm{C}\).
The following applies for the total capacitance:
\[\frac{1}{C_{C}} = \frac {1}{C_1} + \frac{1}{C_2} + \frac{1}{C_{34}},\] \[\frac{1}{C_{C}} = \frac {1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3 + C_4},\] \[\frac {1}{C_{C}} = \frac {(C_3 + C_4)C_2 + (C_3+C_4)C_1 + C_1C_2}{C_1C_2(C_3+C_4)}\]which yields the generic solution after adjusting:
\[{C_\mathrm{C}} = \frac {C_1C_2(C_3+C_4)}{(C_3 + C_4)C_2 + (C_3+C_4)C_1 + C_1C_2}.\]We will utilize the fact that \(C_1 = C_3 \) and \(C_2 = C_4, \) (specifically in this task) which yields:
\[{C_\mathrm{C}} = \frac {C_1C_2(C_1+C_2)}{(C_1 + C_2)C_2 + (C_1+C_2)C_1 + C_1C_2}.\]We factor out \(C_1 + C_2\):
\[{C_\mathrm{C}} = \frac {C_1C_2(C_1+C_2)}{(C_1 + C_2)^2 + C_1C_2}.\]We substitute the known values:
\[{C_\mathrm{C}} = \frac {1 {\cdot} 10\cdot(1+10)}{(1 + 10)^2 + 1 {\cdot} 10}\, µF,\] \[C_\mathrm{C} \doteq 0.84\ µF.\]Solution – Voltage and Charge
We have calculated the total capacitance of the circuit \(C_\mathrm{C} = \frac {C_1C_2(C_1+C_2)}{(C_1 + C_2)^2 + C_1C_2} \doteq 0.84 \ µF\) in the previous section.
We will calculate the total charge from the definition of capacitance \(C = \frac {Q} {U}\):
\[Q_\mathrm{C}= C_C U,\] \[Q_\mathrm{C} = \frac {C_1C_2(C_1+C_2)}{(C_1 + C_2)^2 + C_1C_2} U.\]The charge on capacitors \(C_1, C_2 \) and \( C_{34}\) is the same and is equal to the total charge \(Q_\mathrm{C}\):
\[Q_\mathrm{C} = Q_1 = Q_2 = Q_{34}.\]We will calculate the voltage on every capacitor using the definition of capacitance.
Capacitor \(C_1\)
\[U_1 = \frac {Q_1}{C_1} = \frac {\frac {C_1C_2(C_1+C_2)}{(C_1 + C_2)^2 + C_1C_2}U}{C_1} = \frac {C_2(C_1+C_2)}{(C_1 + C_2)^2 + C_1C_2}U\]Capacitor \(C_2\)
\[U_2 = \frac {Q_2}{C_2}= \frac {\frac {C_1C_2(C_1+C_2)}{(C_1 + C_2)^2 + C_1C_2}U}{C_2} = \frac {C_1(C_1+C_2)}{(C_1 + C_2)^2 + C_1C_2}U\]Capacitor \(C_{34}\)
\[U_{34} = \frac {Q_{34}}{C_{34}}\]We know from previous calculations that \(C_\mathrm{34} = C_3 + C_4 = C_1 + C_2\),
\[U_{34} = \frac {\frac {C_1C_2(C_1+C_2)}{(C_1 + C_2)^2 + C_1C_2}U}{C_1 + C_2} = \frac {C_1C_2}{(C_1 + C_2)^2 + C_1C_2}U.\]Let us prove our calculations. This should apply \(U = U_1 + U_2 + U_{34}\):
\[Left side= U,\] \[Right side= U_1 + U_2 + U_{34} =\frac {C_2(C_1+C_2)}{(C_1 + C_2)^2 + C_1C_2}U + \frac {C_1(C_1+C_2)}{(C_1 + C_2)^2 + C_1C_2}U+\frac {C_1C_2}{(C_1 + C_2)^2 + C_1C_2}U = \] \[=U \frac {C_2(C_1 +C_2) + C_1(C_1+C_2) + C_1C_2}{(C_1 + C_2)^2 + C_1C_2} = U \frac {(C_1 + C_2)^2 + C_1C_2}{(C_1 + C_2)^2 + C_1C_2} = U, \] \[Left side = Right side.\]Capacitors \(C_{3}\) and \(C_{4}\)
Voltage on parallel capacitors is equal, in our case
\[U_3 = U_4 = U_{34}.\]We will calculate charge from the definition of capacitance:
\[Q_3 = U_3 C_3= \frac {C_1C_2}{(C_1 + C_2)^2 + C_1C_2}U C_1 = \frac {C_1^2C_2}{(C_1 + C_2)^2 + C_1C_2}U,\] \[Q_4 = U_4 C_4 = \frac {C_1C_2}{(C_1 + C_2)^2 + C_1C_2}U C_2 = \frac {C_1C_2^2}{(C_1 + C_2)^2 + C_1C_2}U.\]Let us prove our calculations. This should apply \(Q_3 + Q_4 = Q_{34} = Q_C\):
\[Left side = Q_3 + Q_4 = \frac {C_1^2C_2}{(C_1 + C_2)^2 + C_1C_2}U + \frac {C_1C_2^2}{(C_1 + C_2)^2 + C_1C_2}U =\frac {C_1^2C_2 +C_1C_2^2 }{(C_1 + C_2)^2 + C_1C_2}U= \] \[=\frac {C_1C_2(C_1 + C_2)}{(C_1 + C_2)^2 + C_1C_2}U, \] \[Right side = Q_{34}=Q_\mathrm{C} = \frac {C_1C_2(C_1+C_2)}{(C_1 + C_2)^2 + C_1C_2} U, \] \[Left side = Right side\]Substitution of values
\(C_1 = C_3 = 1\ \mu\textrm{F},\ C_2 = C_4 = 10\ \mu\textrm{F},\ U = 100 \textrm{V}. \)
\[Q_\mathrm{C} = Q_1 = Q_2=\frac {C_1C_2(C_1+C_2)}{(C_1 + C_2)^2 + C_1C_2} U =\frac {1 {\cdot} 10\cdot(1+10)}{(1 + 10)^2 + 1{\cdot}10}100\ \mu\textrm{C} \doteq 84\ \mu \textrm{C}.\] \[U_1 = \frac {C_2(C_1+C_2)}{(C_1 + C_2)^2 + C_1C_2}U = \frac {10\cdot(1+10)}{(1 + 10)^2 + 1{\cdot}10}\cdot100\ \textrm{V} \doteq 84\ \textrm{V}.\] \[U_2 = \frac {C_1(C_1+C_2)}{(C_1 + C_2)^2 + C_1C_2}U = \frac {1\cdot(1+10)}{(1 + 10)^2 + 1{\cdot}10}\cdot100\ \textrm{V} \doteq 8.4\ \textrm{V}.\] \[U_{34} =U_3=U_4 = \frac {C_1C_2}{(C_1 + C_2)^2 + C_1C_2}U = \frac {1 {\cdot} 10}{(1 + 10)^2 + 1{\cdot} 10}\cdot100\ \textrm{V} \doteq 7.6\ \textrm{V}. \] \[Q_3 = \frac {C_1^2C_2}{(C_1 + C_2)^2 + C_1C_2}U = \frac {1^2{\cdot}10}{(1 + 10)^2 + 1{\cdot} 10}\cdot100\ \mu\textrm{C} \doteq 7.6 \ \mu\textrm{C}.\] \[Q_4 = \frac {C_1C_2^2}{(C_1 + C_2)^2 + C_1C_2}U = \frac {1 {\cdot} 10^2}{(1 + 10)^2 + 1{\cdot}10}\cdot100\ \mu\textrm{C} \doteq 76 \ \mu\textrm{C}.\]Answer
The total capacitance of the circuit is \(C = 0.84\ µF.\)
Charge and voltage on capacitors:
\[Q_1 = 84\ \mu \textrm{C} \quad U_1 = 84\ V \qquad C_1 = 1 \ \mu\textrm{F}\] \[Q_2 = 84\ \mu \textrm{C} \qquad U_2 = 8.4\ V \qquad C_2 = 10 \ \mu\textrm{F}\] \[Q_3 = 7{,}6\ \mu \textrm{C} \qquad U_3 = 7.6\ V \qquad C_3 = 1 \ \mu\textrm{F}\] \[Q_4 = 76\ \mu \textrm{C} \qquad U_4 = 7.6\ V \qquad C_4 = 10 \ \mu\textrm{F}\]Comment – Results
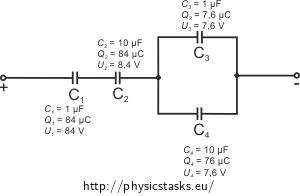
The capacitance of capacitor 4 is ten times bigger than the capacitance of capacitor 3. If we compare charges, we can see that the charge was split in the ratio of the capacitances (the charge on 4 is ten times bigger than the charge on 3). In the same way capacitor 2 has ten times bigger capacitance than capacitor 1. If we compare voltages, we can see that it split in the inverse ratio of capacitances (voltage on 2 is ten times smaller than on 1).




