Field of Charged Spherical Shell

Task number: 1531

A spherical shell with inner radius a and outer radius b is uniformly charged with a charge density ρ.

1) Find the electric field intensity at a distance z from the centre of the shell.

2) Determine also the potential in the distance z.

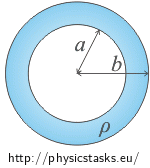
Consider the field inside and outside the shell, i.e. find the behaviour of the electric intensity and the electric potential depending on the variable z in the interval "from zero to infinity".

Hint– Intensity of electric field
Giving the fact that it is useful to apply Gauss's law to solve this problem, it is necessary to decide what to choose for the Gaussian surface.

As a Gaussian surface we choose the surface of a sphere of radius z with its midpoint in the centre of the charged shell. In this case, due to the symmetry of the charge distribution, the vector of electric intensity is at all points perpendicular to the surface and is of the same size.
Let us divide this task into three following cases:
1. The radius of the Gaussian sphere is larger than the outer radius of the charged spherical shell.
2. The radius of the Gaussian sphere is smaller than the outer radius and larger than the inner radius of the charged shell.
3. The radius of the Gaussian sphere is smaller than the inner radius of the charged spherical shell.
Hint–Electric potential
Electric potential is potential energy per unit charge
\[\varphi\,=\, \frac{E_p}{Q}\]
and potential energy E_p at given point is equal to minus the work done by an electric force transferring a charge from the place of zero potential energy (in our case from infinity) to this point.
\[E_p(z)\,=\, - \int^z_{\infty} \vec{F} \cdot \mathrm{d}\vec{z}\]
Now we substitute this integral.
\[\varphi\,=\, - \int^z_{\infty} \frac{\vec{F}} {Q}\cdot \mathrm{d}\vec{z}\]
Force F divided by charge Q is electric field intensity \(\vec{E}\).
\[\varphi\,=\, - \int^z_{\infty} \vec{E}\cdot \mathrm{d}\vec{z}\]
Analysis
Due to the symmetrical charge distribution the simplest way to determine the intensity of electric field is by using Gauss's law. Gauss's law expresses the relationship between the electric flux through a closed surface and a total charge, which is located in the area given by this surface.

The direction of the vector of electric intensity is at all points from the centre of the shell outwards and its magnitude depends only on the distance from the centre of the shell. This is due to the symmetrical distribution of a positive charge in the shell (If the charge were negative, the vectors would be of an opposite direction). To prove this we can use the following idea. The charge is distributed symmetrically in the shell and therefore we cannot see any difference if we turn the spherical shell freely around its centre. The field of the shell must remain the same, and therefore the intensity vector has to be at various rotations still of the same direction and magnitude.

We choose a surface of a sphere to be the Gaussian surface. The sphere is centred in the midpoint of the charged spherical shell. In this case, the vector of electric intensity is on the entire surface of a constant magnitude and is perpendicular to this surface. Thus we simplify the calculation of electric flux.

We divide this task into three parts. We examine separately the field outside the spherical shell, inside the shell and inside the hollow part.

When computing the intensity outside the shell, the radius of the Gaussian sphere is larger than that of the charged shell. Inside it the whole charge is distributed in the shell. The charge is given by the charge density and the volume of the shell.

When calculating the intensity field in the charged shell, the radius of the Gaussian sphere is smaller than the outer radius of the shell and greater than the inner radius of the shell. Only a portion of the charge is closed in the Gaussian surface. The charge closed in the surface is also given by the charge density and the volume of the part of the shell that is closed in the Gaussian surface.

When computing the intensity inside the hollow part of the spherical shell, the radius of the Gaussian sphere is smaller than the inner radius of the shell. Inside the closed area there is no charge, and so the intensity is zero.

The potential is determined by the electric field intensity. The potential at a given point is equal minus the intensity integrated from the place of zero potential to the given point. Zero potential is selected in infinity. (A more detailed explanation is given in the section Hint.)

When calculating the potential inside the charged spherical shell and within the hollow part, we must be careful, because the electric field intensity is not given by the same relation along the path of integration; it is described by different equations outside and inside of the shell and inside the hollow part. Therefore, we must first calculate the work that is needed to transfer the charge to the surface of the charged spherical shell, then the work required to moving the charge within the shell to the edge of the hollow part, and finally the work required for transferring the charge further inside the hollow part.
Solution – Intensity outside the shell
In this section we determine the intensity of the electric field outside the shell, i.e. for z > b.

We use Gauss's law:
\[\oint_S \vec{E} \cdot \mathrm{d}\vec{S}\,=\, \frac{Q}{\varepsilon_0}\,.\] \[\oint_S \vec{E} \cdot \vec{n}\mathrm{d}S\,=\, \frac{Q}{\varepsilon_0}\tag{*}\]
The charge is distributed symmetrically in the spherical shell, and therefore the electric field around the shell is also symmetrical. The vector of electric intensity points at all points from the centre of the shell (or towards the centre, in the case of negative charge) and its size depends only on the distance from the centre of the shell.

We choose the Gaussian surface to be a surface of a sphere with a radius z, its midpoint being the midpoint of the charged shell. In this case, the vector of electric intensity is always perpendicular to the Gaussian surface, and therefore it is true that \(\vec{E} \cdot \vec{n}\,=\,En\,=\,E\) (Note: \(\vec{n}\) is a unit vector).

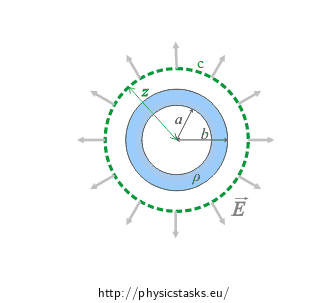
Using this knowledge we can adjust the integral on the left side of the Gauss's law:
\[\oint_c \vec{E} \cdot \vec{n}\mathrm{d}S\,=\,\oint_c E n\mathrm{d}S\,=\, \oint_c E\mathrm{d}S\,.\]
The vector of electric field intensity E is at all points of the Gaussian surface of the same magnitude, so we can factor the electric intensity out of the integral as a constant. We get an equation
\[\oint_c \vec{E} \cdot \vec{n}\mathrm{d}S\,=\,E \oint_c \mathrm{d}S\,.\]
Now we calculate the integral. When integrating dS over a surface of a sphere, we obtain the surface area of the sphere. (Note: We can represent it such that dS are surface areas of small pieces of the sphere surface. If we add all these pieces together, we get the entire surface of the sphere.) The integral is therefore equal to
\[\oint_c \vec{E} \cdot \vec{n}\mathrm{d}S\,=\,E S_s\,,\]
where S_s = 4πz² is the surface of the Gaussian sphere.
\[\oint_c \vec{E} \cdot \vec{n}\mathrm{d}S\,=\,E\, 4 \pi z^2\]
The resulting relationship is substituted back into Gauss's law (*).
\[E 4 \pi z^2\,=\, \frac{Q}{\varepsilon_0}\]
We express the magnitude.
\[E \,=\, \frac{1}{4 \pi \varepsilon_0}\,\frac{Q}{z^2}\tag{**}\]
The formula is the same as the formula for an electric field around a point charge. The field around a charged spherical shell is therefore the same as the field around a point charge.

Finally, we need to evaluate the charge Q inside the Gaussian surface using the given values

Inside the Gaussian surface there is the whole charged shell, thus the charge can be evaluated through the shell volume V and the charge density ρ.
\[Q\,=\,V \varrho\,=\,\frac{4}{3} \pi \left(b^3 - a^3\right) \varrho\]
After substituting into the formula (**) and adjusting we obtain
\[E \,=\, \frac{1}{4 \pi \varepsilon_0}\,\frac{\frac{4}{3} \pi \left(b^3 - a^3\right) \varrho}{z^2}\,=\, \frac{\varrho \left(b^3 - a^3\right)}{3 \varepsilon_0\,z^2}\]
At a distance z the electric field intensity of the charged shell is:
\[E \,=\, \frac{\varrho \left(b^3 - a^3\right)}{3 \varepsilon_0} \, \frac{1}{z^2}\,. \]
Solution – Intensity inside the charged shell
In this section we evaluate the intensity of the electric field inside the charged spherical shell (a < z < b ). The procedure is very similar to the previous section: The intensity outside the charged shell, therefore this solution is not described in detail.

We determine the electric field intensity by using Gauss's law:
\[\oint_c \vec{E} \cdot \mathrm{d}\vec{S}\,=\, \frac{Q_1}{\varepsilon_0}\,,\tag{*}\]
where Q₁ is the charge closed inside the Gaussian surface.

We choose the Gaussian surface to be a surface of a sphere, which is centred in the midpoint of the charged sphere and its radius is z, a < z < b.

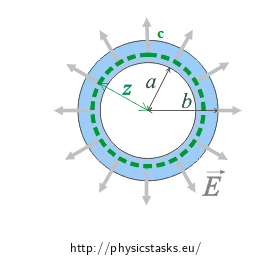
Using the same reasoning about symmetry as in the previous section, we obtain that the intensity vector is of the same magnitude and perpendicular to the Gaussian surface at all points of the Gaussian surface, therefore the following applies:
\[\oint_c \vec{E} \cdot \mathrm{d}\vec{S}\,=\,\oint_c En \mathrm{d}S\,=\,\oint_c E \mathrm{d}S\,=\,E\oint_c \mathrm{d}S\,,\]
where the last integral is equal to the surface of the Gaussian sphere.
\[\oint_c \vec{E} \cdot \mathrm{d}\vec{S}\,=\,E\, 4 \pi z^2\,\]
Now we evaluate the charge Q₁. Since the Gaussian sphere is smaller than the charged spherical shell, there is only a part of the charge enclosed in the Gaussian sphere. Thus, the charge is evaluated using the charge density and a volume of the sphere part enclosed in the Gaussian sphere
\[Q_1\,=\,V_1 \varrho \,=\, \frac{4}{3} \pi \left(z^3-a^3\right) \varrho\,.\]
We substitute both gained relations into Gauss's law (*)
\[E \,4\pi z^2\,=\, \frac{\frac{4}{3} \pi \left(z^3-a^3\right)\varrho}{\varepsilon_0}\]
and evaluate the magnitude of the electric field inside the charged spherical shell.
\[E \,=\, \frac{\varrho}{3 \varepsilon_0}\,\frac{z^3-a^3}{z^2} \,=\, \frac{\varrho}{3 \varepsilon_0}\,\left(z-\frac{a^3}{z^2} \right) \]
Solution – Intensity inside the hollow part
The intensity of the electric field inside the hollow part of the charged shell (z < a) can be determined again by using Gauss's law.
\[\oint_S E \cdot \mathrm{d}S \,=\, \frac{Q}{\epsilon_0}\,,\]
where Q is the charge enclosed inside the Gaussian surface

For a Gaussian surface we choose again the surface of a sphere centred in the midpoint of the charged shell with radius z. The intensity flow through this area (i.e. the left side of Gauss's law) is determined exactly the same way as in the previous cases.

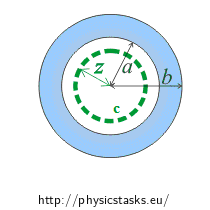
Since this selected area is within the charged shell, no charge is enclosed in it, i.e Q = 0.

Adjusting the left side of Gauss's law is the same as in previous sections. After substituting the zero charge it is obvious, that the electric field intensity is zero.

The magnitude of the electric field inside the sphere is equal to zero.
Solution – Potential outside of the charged shell
Electric potential at point A is equal to a negative taken integral of intensity from a point of zero potential to the point A. The zero potential is selected in infinity. (A more detailed explanation is given in the section Hint.)
\[\varphi (z)\,=\, - \int_{\infty}^z \vec{E} \cdot \mathrm{d}\vec{z}\]
Giving the fact, that the electric field intensity depends only on the distance from the centre of the shell, the potential is also dependent only on the distance z from the centre of the shell.

The potential does not depend on the choice of the integration curve; therefore it can be freely selected. (We choose such curve that the integral is simple.) In this task for an integration curve we choose a part of a line leading through the midpoint of the sphere.

The vector of electric field intensity \(\vec{E}\) is parallel to the vector \(\vec{z}\). Therefore, we can simplify the integral.
\[ \varphi (z)\,=\, - \int^{z}_{\infty} E \mathrm{d}z \]
Now we have to divide the task into three separate cases and calculate the potential outside the shell, inside the shell and inside the hollow part.

First, we express the potential at a distance z outside the shell.
\[\varphi (z)\,=\, - \int^{z}_{\infty} E \mathrm{d}z \]
We substitute the magnitude of the electric intensity in the integral. The intensity is evaluated in the section: Intensity outside the shell
\[E \,=\, \frac{\varrho \left(b^3-a^3\right)}{3 \varepsilon_0}\,\frac{1}{z^2}\] .
We factor all constants out of the integral.
\[\varphi (z)\,=\, - \int^{z}_{\infty} \frac{\varrho \left(b^3-a^3\right)}{3 \varepsilon_0}\,\frac{1}{z^2} \,\mathrm{d}z \,=\, - \,\frac{\varrho \left(b^3-a^3\right)}{3 \varepsilon_0} \int^{z}_{\infty} \frac{1}{z^2}\, \mathrm{d}z\]
Now we calculate the definite integral.
\[\varphi (z)\,=\,- \,\frac{\varrho \left(b^3-a^3\right)}{3 \varepsilon_0}\,\left[- \frac{1}{z}\right]^z_{\infty}\,.\]
We substitute the limits of the integral and obtain the size of the potential outside the shell at distance z:
\[\varphi (z)\,=\,\frac{\varrho \left(b^3-a^3\right)}{3 \varepsilon_0}\,\frac{1}{z}\,.\]
Note: If we substitute the total charge \(Q\,=\, \frac{4}{3}\pi \left(b^3-a^3\right)\varrho\) in the equation, we obtain the same relation as the relation for the potential around a point charge.
\[ \varphi (z)\,=\, \frac{Q}{4 \pi \varepsilon_0}\,\frac{1}{z}\]
Solution – Potential inside the shell
When calculating the potential inside the sphere we proceed as in the previous section. The potential is represented by the equation: \[ \varphi (z)\,=\, - \int^{z}_{\infty} \vec{E} \cdot \mathrm{d}\vec{z}\,=\, - \int^{z}_{\infty} E \mathrm{d}z \,.\]
When evaluating the potential we need to take into account the magnitude of the electric field intensity. This time the electric field intensity is not represented along the integral curve by the same relation. The relation for intensity changes on the surface of the shell. Therefore, the entire integral is divided into two parts. First we have to transfer the charge from infinity to the surface of the shell (i.e. to distance b from the centre of the shell) and then from the surface of the shell further inside the shell.
\[\varphi (z)\,=\, - \int^{b}_{\infty} E_v \mathrm{d}z - \int^{z}_{b} E_u \mathrm{d}z \]
We substitute the relevant size of intensity, which we have evaluated in previous sections. Thus we obtain
\[\varphi (z)\,=\, - \int^{b}_{\infty} \frac{\varrho \left(b^3-a^3\right)}{3 \varepsilon_0}\, \frac{1}{z^2}\, \mathrm{d}z \, - \int^{z}_{b} \frac{ \varrho}{3 \varepsilon_0\,}\, \left(z-\frac{a^3}{z^2}\right) \, \mathrm{d}z \,.\]
We can factor constants out of the integral
\[\varphi (z)\,=\, - \frac{\varrho \left(b^3-a^3\right)}{3 \varepsilon_0}\int^{b}_{\infty} \frac{1}{z^2}\, \mathrm{d}z \,- \,\frac{ \varrho}{3 \varepsilon_0\,}\int^{z}_{b} \left(z-\frac{a^3}{z^2}\right)\, \mathrm{d}z \,,\]
Then we divide the second integral into two integrals:
\[\varphi (z)\,=\, - \frac{\varrho \left(b^3-a^3\right)}{3 \varepsilon_0}\int^{b}_{\infty} \frac{1}{z^2} \,\mathrm{d}z \,-\, \frac{ \varrho}{3 \varepsilon_0\,}\int^{z}_{b} z\, \mathrm{d}z \, + \,\frac{ \varrho}{3 \varepsilon_0\,}\int^{z}_{b} \frac{a^3}{z^2}\, \mathrm{d}z\,,\]
and calculate the integrals. (Note: We did not need to evaluate the first integral, we could have substituted z = b into the outcome of the previous section)
\[\varphi (z)\,=\, - \frac{\varrho \left(b^3-a^3\right)}{3 \varepsilon_0}\,\left[- \frac{1}{z}\right]^b_{\infty}- \,\frac{ \varrho}{3 \varepsilon_0\,}\left[\frac{z^2}{2}\right]^z_{b} + \,\frac{ \varrho}{3 \varepsilon_0\,}\left[-\frac{a^3}{z}\right]^z_{b}\,.\]
By substituting the limits of the integrals we obtain
\[\varphi (z)\,=\,- \frac{\varrho \left(b^3-a^3\right)}{3 \varepsilon_0}\left(- \frac{1}{b}\right)\,- \,\frac{ \varrho}{3 \varepsilon_0\,}\left(\frac{z^2}{2}-\frac{b^2}{2}\right) \,+ \,\frac{ \varrho}{3 \varepsilon_0\,}\left( -\frac{a^3}{z}\,+\frac{a^3}{b}\right)\,.\]
We need to adjust this relation to simplify the result. We multiply the parentheses and add the same components together.
\[\varphi (z)\,=\,\frac{\varrho \left(b^3-a^3\right)}{3 \varepsilon_0} \frac{1}{b}\,- \,\frac{ \varrho}{3 \varepsilon_0}\left(\frac{z^2}{2}-\,\frac{b^2}{2}\right) \,+ \,\frac{ \varrho}{3 \varepsilon_0\,}\left( -\frac{a^3}{z}\,+\frac{a^3}{b}\right)\] \[\varphi (z)\,=\, \frac{\varrho b^3}{3 \varepsilon_0\, b} \,-\,\frac{\varrho a^3}{3 \varepsilon_0 b} \,-\,\frac{ \varrho z^2}{6 \varepsilon_0} \,+\,\frac{ \varrho b^2}{6 \varepsilon_0} \,- \,\frac{ \varrho a^3}{3 \varepsilon_0 \,z } \,+ \,\frac{ \varrho a^3}{3 \varepsilon_0\, b}\]
We divide the first component by b and we add the fourth and the second component to the last component.
\[\varphi (z)\,=\, \frac{\varrho b^2}{2 \varepsilon_0} \,-\,\frac{ \varrho z^2}{6 \varepsilon_0} \,- \,\frac{ \varrho a^3}{3 \varepsilon_0 \,z } \] \[\varphi (z)\,=\, \frac{\varrho b^2}{2 \varepsilon_0} \,-\,\frac{ \varrho }{3 \varepsilon_0} \left( \frac{ z^2}{2 } +\,\frac{ a^3}{z}\right) \]
Thus we obtain the equation for potential inside the charged shell.
Solution – Potential inside the hollow part
When calculating the potential inside the hollow part we proceed as in the previous section. The potential is represented by the equation:
\[ \varphi (z)\,=\, - \int^{z}_{\infty} \vec{E} \cdot \mathrm{d}\vec{z}\,=\, - \int^{z}_{\infty} E \mathrm{d}z \,.\]
When evaluating the potential we need to take into account the magnitude of the electric intensity. This time the electric field intensity is not represented by the same relation along the integral curve.

Inside the hollow part of the shell the electric field intensity is zero, therefore when extending the integration curve inside the hollow part the potential does not change. The potential therefore remains constant and of the same value as on the inner surface of the shell.

We substitute z = a into the result of the previous section.
\[\varphi (z)\,=\, \frac{\varrho b^2}{2 \varepsilon_0} \,-\,\frac{ \varrho }{3 \varepsilon_0} \left( \frac{ z^2}{2 }+\,\frac{ a^3}{z}\right) \,=\,\frac{\varrho b^2}{2 \varepsilon_0} \,-\,\frac{ \varrho }{3 \varepsilon_0} \left( \frac{ a^2}{2 } +\,\frac{ a^3}{a}\right)\]
We adjust the expression in parentheses.
\[ \varphi (z)\,=\, \frac{\varrho b^2}{2 \varepsilon_0} \,-\,\frac{ \varrho }{3 \varepsilon_0} \left( \frac{ a^2}{2 } +\, a^2 \right)\,=\, \frac{\varrho b^2}{2 \varepsilon_0} \,-\,\frac{ \varrho }{3 \varepsilon_0} \frac{ 3a^2}{2 }\,=\, \frac{\varrho b^2}{2 \varepsilon_0} \,-\,\frac{ \varrho a^2}{2 \varepsilon_0} \]
We factor \( \frac{\varrho}{2 \varepsilon_0}\) and we obtain a relation for calculating the potential inside the hollow part of the charged spherical shell.
\[ \varphi (z)\,=\,\frac{\varrho}{2 \varepsilon_0} \left(b^2-a^2\right)\]
Answer
In all cases, the vector of electric field intensity points from or toward the centre of the spherical shell (depending on the sign of the charge).

The magnitude of electric field intensity outside the charged spherical shell (z > b) is given by
\[E \,=\, \frac{\varrho \left(b^3 - a^3\right)}{3 \varepsilon_0} \, \frac{1}{z^2}\,=\, \frac{Q}{4 \pi \varepsilon_0} \, \frac{1}{z^2} \,.\]
The magnitude of electric field intensity inside the shell (a < z < b) is given by
\[E \,=\, \frac{\varrho}{3 \varepsilon_0}\,\left(z-\frac{a^3}{z^2} \right) \,.\]
The magnitude of electric field intensity inside the hollow part (z < a) equals to zero.

The electric potential outside the charged spherical shell is given by
\[\varphi (z)\,=\,\frac{\varrho \left(b^3-a^3\right)}{3 \varepsilon_0}\,\frac{1}{z}\,=\, \frac{Q}{4 \pi \varepsilon_0} \, \frac{1}{z}\,.\]
The electric potential inside the spherical shell is given by
\[\varphi (z)\,=\, \frac{\varrho b^2}{2 \varepsilon_0} \,-\,\frac{ \varrho }{3 \varepsilon_0} \left( \frac{ z^2}{2 }+\,\frac{ a^3}{z}\right)\,. \]
The electric potential inside the hollow part of the spherical shell is constant and is equal to
\[ \varphi (z)\,=\,\frac{\varrho}{2 \varepsilon_0} \left(b^2-a^2\right)\,.\]
Graphs
Graph of the magnitude of electric intensity as a function of the distance from the centre of the spherical shell:

The intensity inside the hollow part (z < a) equals to zero.

The magnitude of electric field intensity inside the shell (a < z < b) is
\[E \,=\, \frac{\varrho}{3 \varepsilon_0}\,\left(z-\frac{a^3}{z^2} \right) \,.\]
The magnitude of electric field intensity outside the charged spherical shell (z > b) is
\[E \,=\, \frac{\varrho \left(b^3 - a^3\right)}{3 \varepsilon_0} \, \frac{1}{z^2} \,.\]
The function is continuous. The first part of the graph (for z from 0 to a) is a constant function passing through the origin. The intensity increases over the interval a to b and then in the distance z greater than bthe intensity decreases with the square of the distance z.

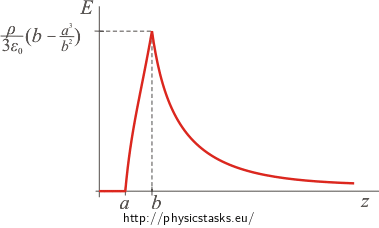
Note: The electric field intensity is continuous with the exception of the points on the charged surfaces, which are not included in this task.

Graph of the electric potential as a function of the distance from the centre of the shell:

The electric potential inside the hollow part of the spherical shell is constant and is equal to
\[ \varphi (z)\,=\,\frac{\varrho}{2 \varepsilon_0} \left(b^2-a^2\right)\,.\]
The electric potential inside the charged spherical shell is equal to
\[\varphi (z)\,=\, \frac{\varrho b^2}{2 \varepsilon_0} \,-\,\frac{ \varrho }{3 \varepsilon_0} \left( \frac{ z^2}{2 }+\,\frac{ a^3}{z}\right)\,. \]
The electric potential outside the charged spherical shell is given by
\[\varphi (z)\,=\,\frac{\varrho \left(b^3-a^3\right)}{3 \varepsilon_0}\,\frac{1}{z}\,.\]
The function is in point z = a and z = b continuous. In these points the function has a continuous first derivative; therefore the function is smooth in these points.

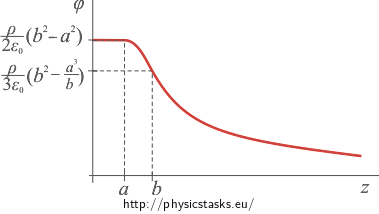
Note: The electric potential is always continuous, because it is actually work done by transferring a unit charge and it cannot be changed "by steps". Aside from the charged surfaces, the potential also has continuous first derivative, i.e. it is smooth.
What is the relation between a charged spherical shell and a charged ball
We can evaluate the electric field intensity of a charged ball by using the above derived results. If we reduce the hollow part of the charged shell until a = 0 and denote b = R, we obtain a ball of radius R charged with charge density ρ.

We substitute a = 0 and b = R, into the relations and we obtain the same result as in the task Pole rovnoměrně nabité koule.

The intensity outside the ball:
\[E\,=\, \frac{\varrho\left( R^3-0\right)}{3 \varepsilon_0} \, \frac{1}{z^2} \,=\, \frac{\varrho R^3}{3 \varepsilon_0} \, \frac{1}{z^2} \]
The intensity inside the ball:
\[E \,=\, \frac{\varrho}{3 \varepsilon_0}\,\left(z-\frac{0}{z^2}\right)\,=\, \frac{\varrho}{3 \varepsilon_0}\,z \]
The potential outside the ball:
\[\varphi(z)\,=\, \frac{\varrho\left( R^3-0\right)}{3 \varepsilon_0} \, \frac{1}{z} \,=\, \frac{\varrho R^3}{3 \varepsilon_0} \, \frac{1}{z}\,.\]
The potential inside the ball:
\[\varphi (z)\,=\, \frac{\varrho R^2}{2 \varepsilon_0} \,-\,\frac{ \varrho }{3 \varepsilon_0} \left( \frac{ z^2}{2 }+\,\frac{ 0^3}{z}\right)\,=\, \frac{\varrho R^2}{2 \varepsilon_0} \,-\,\frac{ \varrho z^2}{6 \varepsilon_0} \] \[\varphi (z)\,=\, \frac{\varrho R^2}{6 \varepsilon_0} \left(3-\frac{ z^2}{R^2} \right) \,. \]
We see that the relations are the same.
What is the relation between a charged spherical shell and a charged sphere
The sphere is actually a very thin spherical shell. If we enlarge the hollow part inside the shell until a = b = R, we obtain a sphere of radius R. Instead of charge bulk density, we consider area density. The relation between area density and bulk density is
\[\sigma\,=\,\varrho \mathrm{\Delta}R\]
where ΔR is the thickness of the sphere and therefore ΔR = b−a.

We adjust the formula for intensity outside the sphere in such a way that we can factor out the relation for area density. We factor the expression in parentheses.
\[E \,=\, \frac{\varrho \left(b^3 - a^3\right)}{3 \varepsilon_0} \, \frac{1}{z^2} \,=\, \frac{\varrho \left(b - a\right) \left(b^2 +ba+ a^2\right)}{3 \varepsilon_0} \, \frac{1}{z^2} \]
The first parenthesis in the numerator is equal to the thickness of the sphere ΔR.
\[E \,=\, \frac{\varrho \mathrm{\Delta}R \left(b^2 +ba+ a^2\right)}{3 \varepsilon_0} \, \frac{1}{z^2}\,=\, \frac{\sigma \left(b^2 +ba+ a^2\right)}{3 \varepsilon_0} \, \frac{1}{z^2} \]
By substituting a = b = R, we get
\[E \,=\, \frac{\sigma \left(R^2 +R^2+ R^2\right)}{3 \varepsilon_0} \, \frac{1}{z^2}\,=\, \frac{\sigma 3R^2 }{3 \varepsilon_0} \, \frac{1}{z^2} \,=\, \frac{\sigma R^2 }{ \varepsilon_0} \, \frac{1}{z^2}\]
We have obtained a relation for evaluating the electric field intensity outside the charged sphere.

The intensity inside the sphere is zero.

When calculating the potential outside the sphere we need to adjust the formula again, so that it includes the area density. The expression in the parentheses is factored as in the case of electric intensity.
\[\varphi (z)\,=\,\frac{\varrho \left(b^3-a^3\right)}{3 \varepsilon_0}\,\frac{1}{z}\,=\,\frac{\varrho \left(b - a\right) \left(b^2 +ba+ a^2\right)}{3 \varepsilon_0}\frac{1}{z}\] \[\varphi (z)\,=\, \frac{\varrho \mathrm{\Delta}R \left(b^2 +ba+ a^2\right)}{3 \varepsilon_0} \, \frac{1}{z}\,=\, \frac{\sigma \left(b^2 +ba+ a^2\right)}{3 \varepsilon_0} \, \frac{1}{z}\,.\]
By substituting a = b = R we get
\[\varphi (z)\,=\, \frac{\sigma \left(R^2 +R^2+ R^2\right)}{3 \varepsilon_0} \, \frac{1}{z}\,=\, \frac{\sigma 3 R^2}{3 \varepsilon_0} \, \frac{1}{z}\,.\] \[\varphi (z)\,=\, \frac{\sigma R^2}{ \varepsilon_0} \, \frac{1}{z}\,.\]
Now it remains to evaluate the potential inside the sphere. First, we factor the expression in the parentheses.
\[ \varphi (z)\,=\,\frac{\varrho \left(b^2-a^2\right)}{2 \varepsilon_0} \,=\,\frac{\varrho \left(b-a\right)\left(b+a\right)}{2 \varepsilon_0} \,=\,\frac{\varrho \mathrm{\Delta}R \left(b+a\right)}{2 \varepsilon_0}\,=\,\frac{\sigma \left(b+a\right)}{2 \varepsilon_0}\,.\]
By substituting a = b = R we get
\[ \varphi (z)\,=\,\frac{\sigma \left(R+R\right)}{2 \varepsilon_0}\,=\,\frac{\sigma 2R}{2 \varepsilon_0}\] \[ \varphi (z)\,=\,\frac{\sigma R}{ \varepsilon_0}\,.\]
Link to related tasks
A very thin sphere is a special case of charged spherical shell and it is described in a task Pole rovnoměrně nabité sféry. A ball is also a special case of charged spherical shell and it is described in the task Pole rovnoměrně nabité koule. Both tasks are more simple to calculate.