Collection of Solved Problems in Physics

Force Acting on Capacitor Plates

Task number: 1535

• Figure

  

• Hint: Electric field intensity

  The intensity of a uniform field between the plates is given by the voltage between the plates and their distance. Both plates contribute to this intensity equally.

• Hint: Force

  The force applied by one plate on the other depends on the charge of the first plate and on the magnitude of the electric field intensity vector generated by the second plate.

• Analysis: Force applied to the capacitor plates

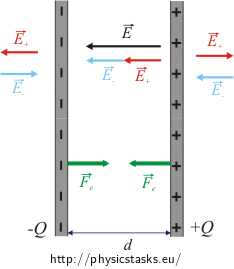
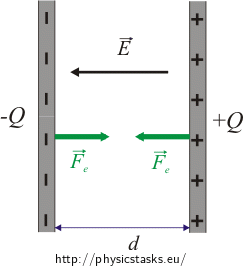
  The charge Q is uniformly distributed on the capacitor plates. One plate is charged positively, the other negatively; therefore both plates are attracted to each other by an electric force.

  The force acting on the first plate is proportional to the charge of the plate and to the electric field that is generated by the second plate (electric field generated by the first plate does not act on the plate itself).

  The intensity of the uniform field of the capacitor is given by the vector sum of the intensities of the two plates. The sign of the plate charge affects the direction of the electric intensity vector; whether it points outward or toward the plate. The direction of both vectors is the same between the plates, outside the capacitor the vectors cancel each other out. The electric field intensity of the first plate is therefore half the total electric field intensity inside between the capacitor plates.

  

• Solution: Force acting on the capacitor plates

  We determine the force acting on the negatively charged plate using this equation:

  \[F_-\,=\,QE_+\,,\]

  where Q is the charge of the negatively charged plate, E₊ is the magnitude of electric intensity "of the positively charged plate".

  Similarly, we determine the force acting on the positively charged plate as:

  \[F_+\,=\,QE_-\]

  Both forces are of the same magnitude. Their magnitude will hereafter be referred to as F_e.

  Both \(\vec{E}_+\) and \(\vec{E}_-\) vectors are between the plates of the same magnitude and also of the same direction. Therefore we can write

  \[E_+\,=\,E_-\,=\,\frac{E}{2}\,,\]

  where E is the magnitude of the overall electric field intensity between the capacitor plates.

  The electric field inside the capacitor is given by:

  \[E\,=\,\frac{U_1}{d}\]

  We substitute the intensity into the equation for electric force:

  \[F_e \,=\, Q\frac{E}{2}\,=\,Q\frac{U_1}{2d}\]

  We obtain the charge of the plate capacitor by using the capacitance and the voltage and the formula \(Q=C_1U_1\).

  \[ F_e\,=\,\frac{C_1U_1^2}{2d}\tag{*}\]

  Now we need to determine the capacitance of the capacitor, which depends on the surface area of the plates, the permittivity of the material between the plates and the distance of the plates:

  \[C_1\,=\,\frac{\varepsilon S}{d}\]

  Note: The permitivity \(\varepsilon\) is the absolute permitivity of the material between the plates of the capacitor. It is equal to the product of the relative permitivity of the material \(\varepsilon_r\) and the permittivity of vacuum. \(\varepsilon_0\).

  We substitute the capacitance into (*) and we evaluate the force acting on the capacitor plates.

  \[F_e\,=\,\frac{\varepsilon S U_1^2}{2d^2}\]

• Hint: Work applied when moving the plates

  The work done when moving the plates depends on the force we need to overcome, and the distance by which the plates were moved.

• Hint: What quantities change when we move the plates

  When the capacitor is disconnected from the source, the charge remains constant. By changing the distance of the plates, we change the capacitance of the plates and hence the voltage.

• I. Analysis: Work applied when moving the plates

  The work that needs to be done when moving the plates to the distance 2d depends on the force we need to overcome, and the distance by which the plates are moved.

  The plates are moved the distance 2d, we moved them by a distance d.

  When moving the plates we need to overcome the electric force attracting the plates. (We determined this force in the previous section: Force acting on the capacitor plates). When we move the plates, the charge of the plates does not change, however the voltage does (the capacitor is disconnected from the power supply). We can therefore express the force using the electric charge.

• I. Solution: Work applied when moving the plates

  When moving the plates we need to overcome an electric force F_e attracting the plates. We have evaluated the force in the previous section Solution: Force acting on the capacitor plates

  \[F_e\,=\,\frac{\varepsilon S U_1^2}{2d^2}\]

  When moving the plates apart, the voltage between them changes but their charge remains the same, because the capacitor is disconnected from the power supply. Therefore, we need to express the electric force acting on the plates by such variables that remain unchanged during the movement, i.e. the charge and surface of the plates.

  \[F_e\,=\,\frac{\varepsilon S {\left( \frac{Q}{C_1}\right)}^2}{2d^2}\,=\,\frac{\varepsilon S }{2d^2} \,\frac{Q^2}{C_1^2}\,=\,\frac{\varepsilon S }{2d^2} \,\frac{Q^2d^2}{\varepsilon^2 S^2}\,=\,\frac{Q^2}{2\varepsilon S}\]

  We can see that the force does not depend on the distance d when moving the plates. We can determine the work applied by using this relation:

  \[W\,=\,Fd\,,\]

  where d is the distance by which the capacitor plates are moved.

  After substituting the evaluated force we obtain the relationship for applied work:

  \[W\,=\,\frac{Q^2}{2\varepsilon S}d\]

  We can express the charge through the initial voltage and capacitance \(Q=C_1U_1\).

  \[W\,=\,\frac{C_1^2 U_1^2d}{2\varepsilon S}\,=\,\frac{\varepsilon_0^2 S^2 U_1^2 d}{2\varepsilon S d^2}\]

  After adjusting the expression we obtain the work applied when moving the plates twice the distance d.

  \[W\,=\,\frac{\varepsilon S U_1^2}{2d}\]

• II. Analysis: Determination of applied work using the conservation of energy

  If we move the plates apart, energy is conserved. The work applied is therefore equal to a difference of electric energy before and after moving the plates.

  Electric energy of a capacitor depends on the permittivity, the square of voltage, the surface of the plates and the distance between the plates.

• II. Solution: Determination of applied work using the conservation of energy

  Initially, the capacitor energy is equal to:

  \[E_1\,=\,\frac{1}{2}\,C_1 U_1^2\]

  When moving the plates apart, the voltage changes; we therefore express the voltage through the capacitor charge, which remains constant \(U_1\,=\,\frac{Q}{C_1}\)

  \[E_1\,=\,\frac{1}{2}\,C_1 \frac{Q^2}{C_1^2}\,=\,\frac{1}{2}\, {\frac{Q^2}{C_1}}\]

  The capacitor energy is therefore:

  \[E_1\,=\,\frac{1}{2}\, {\frac{Q^2d}{\varepsilon S}}\tag{1}\]

  When moving the plates, the energy increases because the distance of the plates is now 2d:

  \[E_2\,=\,\frac{1}{2}\, {\frac{Q^2}{C_2}}\,=\,\frac{1}{2} \,{\frac{Q^2 2d}{\varepsilon S}}\,=\,\ {\frac{Q^2 d}{\varepsilon S}}\tag{2}\]

  The law of conservation of energy applies. The work applied is equal to the difference of electric energy before and after moving the plates.

  \[W\,=\,E_2-E_1\]

  We substitute the relations (1) and (2) for energy E₁ and E₂.

  \[W\,=\,{\frac{Q^2 d}{\varepsilon S}} \,-\,\frac{1}{2} \,{\frac{Q^2d}{\varepsilon S}}\,=\,\frac{1}{2} \,{\frac{Q^2d}{\varepsilon S}}\]

  Now we express charge through the given initial voltage and capacitance.

  \[W\,=\,\frac{1}{2} \,{\frac{ \left( C_1 U_1 \right)^2 d}{\varepsilon S}}\,=\,\frac{1}{2} \,{\frac{ \varepsilon^2 S^2 \, U_1^2 \, d}{d^2 \, \varepsilon S}}\,=\,{\frac{ \varepsilon S \, U_1^2}{2d}}\]

• Answer

  The force acting on the capacitor plates is

  \[F_e=\frac{\varepsilon S U_1^2}{2d^2}\,\,.\]

  The work applied when moving the plates apart twice the distance is

  \[W=\frac{\varepsilon S U_1^2}{2d}\,\,.\]