A charged droplet between two charged plates
Task number: 2141
A small, negatively charged oil droplet weighing 10−13 kg is hovering still in the space between two charged horizontal plates that are 4.8 mm apart and have a voltage of 1 kV between them.
(a) What amount of electric charge does the droplet hold?
(b) How many excess electrons does the negatively charged oil droplet have?
(c) How many electrons had the drop lost from the total number of its excess electrons if it started to move downwards with an acceleration of 5 m·s−2?
Hint for part (a)
What forces act on the oil droplet? What is the balance between the forces if the droplet is at rest?
Hint (a): Homogeneous electric field
The electric field between the two horizontal charged plates depends on the distance between the plates and on the voltage between them. The further apart the plates are from each other, and the lower is the voltage between them, the weaker is the electric field between the plates.
Analysis (a): The charge of the droplet
The oil droplet is pulled upwards by the electrostatic force and downwards by the gravitational force. These two forces must have the same size and opposite direction when the droplet is at rest.
The charge of the droplet, which we want to determine, can be calculated from the magnitude of the electrostatic force. This force is proportional to the strength of the electric field between the plates.
The electric field between the horizontal charged plates is directly proportional to the voltage between the plates and inversely proportional to the distance between the plates.
Solution (a): The charge of the drop
The electric force Fe = Q·E acts upwards on the oil droplet and the gravitational force FG = m·g acts downwards on it , where E is the electric field between the plates, Q is the charge of the droplet and m is its weight.
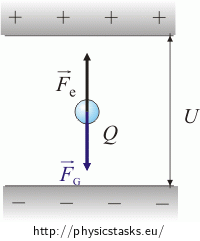
Because the drop is at rest, the opposing forces must have equal magnitudes.
\[F_G \,=\,F_e\] \[mg \,=\, QE\]The following relationship applies for the homogeneous electric field E between the plates:
\[E \,=\, \frac{V}{d}\,.\]We substitute this formula to the previous relationship and we express the charge of the drop Q.
\[mg \,=\, Q\,\frac{V}{d}\] \[Q \,=\, \frac {mgd}{V}\]Hint (b): Number of electrons
We can find the charge of an electron in the tables and calculate the number of excess electrons from the the total charge that we have calculated in section a).
Solution (b): the number of electrons
The negative charge of the drop that we have calculated in section (a) is carried by the excess electrons.
We can calculate the number N of these electrons because the we can find out the charge e of a single electron.
\[N \,=\, \frac {Q}{e}\] \[N \,=\, \frac {mgd}{Ve}\]Help on part (c)
1) Which of the forces acting on the droplet have changed when the droplet has lost some of its charge?
2) The drop moves with an acceleration, so we can use 2nd Newton’s law.
Analysis of part (c)
If the drop loses several electrons, its charge decreases and therefore the upward force of the surrounding electric field on the drop is reduced. The gravitational force remains the same because the weight of the drop does not change (the weight of the electron is very small, so we neglect the change in the drop weight). The resulting force calculated from the electric and gravitational forces aims downwards. This resulting force gives the drop an acceleration (proportional to its weight) according to the 2nd Newton’s law and the droplet therefore begins to move downwards.
Solution of part (c)
When the drop loses several electrons, its charge reduces from Q to Q1. The new magnitude of the electrostatic force is Fe1 = Q1E
The resulting force after subtracting electrostatic and gravitational force is equal to the FG−Fe1
We determine the acceleration of the drop from the second Newton’s law.
\[F_g-{F_{e}}_1 \,=\, m a\tag{*}\]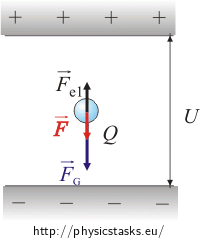
For a homogeneous electric field, the same relationship applies as in the solution of part (a):
\[E \,=\, \frac {V}{d}\]We substitute the formulas for FG, Fe1 and E into the relationship (*):
\[m g-Q_1 E \,=\, m g\] \[m g-Q_1 \frac{V}{d} \,=\, m a\]and we factor out the charge Q1 from the expression.
\[Q_1 \frac{V}{d} \,=\, m g-m a\] \[Q_1 \,=\, \frac {m(g-a)d}{V}\]We can simply find out the number of excess electrons on the droplet from the new chage of the droplet the same way as in part (b):
\[N_1 \,=\, \frac{Q_1}{e}=\frac {m(g-a)d}{Ve}\]We get the number of electrons that the drop lost as the difference between the original and the new count
\[\Delta N\,=\,N-N_1\] \[\Delta N\,=\,\frac {mgd}{Ve}\,-\,\frac {m(g-a)d}{Ve}\] \[\Delta N\,=\,\frac {mad}{Ve}\]Notation and numerical calculation
\(d\,=\,4.8 \,\mathrm{mm}\,=\,4.8{\cdot} 10^{-3} \,\mathrm{m}\) Distance between the plates \(V\,=1\,\mathrm{kV}\,=\,10^3 \,\mathrm{V}\) Voltage between the plates \(m\,=\,10^{-13} \,\mathrm{kg}\) Oil droplet weight \(a\,=\,5 \,\mathrm{m\,s^{-2}}\) Drop acceleration \(Q\,=\,?\,\left(\mathrm{C}\right)\) Charge of the droplet \(N\,=\,?\) Number of excess electrons on the still droplet \(\Delta N\,=\,?\) Change of electron cound on the moving droplet From tables:
\(e\,=\,1{,}6 {\cdot} 10^{-19}\,\mathrm{C}\) \(g\,=\,9.81\,\mathrm{ m\,s^{-2}}\)
\[Q\,=\,\frac {mgd}{V}\,=\,\frac {10^{-13}\,\cdot \,9.81\,\cdot \,4.8{\cdot} 10^{-3}}{10^3}\,\mathrm{C}\,=\,4.8\cdot{10^{-18}}\,\mathrm{C}\] \[N\,=\,\frac {mgd} {Ve}\,=\,\frac {10^{-13}\,\cdot \,9.81\,\cdot\, 4.8{\cdot} 10^{-3}}{10^3\,\cdot\, 1.6 {\cdot} 10^{-19} }=30\] \[\Delta N\,=\,\frac {mad}{Ve}\,=\,\frac {10^{-13}\,\cdot \,5\,\cdot \,4.8{\cdot} 10^{-3}}{10^3\,\cdot\, 1.6 {\cdot} 10^{-19}}\,=\,15\]The answer
The oil droplet has a charge of 4.8·10 −18 C, which is carried by 30 excess electrons.
The droplet began to move with the given acceleration after it had lost 15 electrons.
Measuring the elementary charge
The elementary charge e was first measured directly by the American physicist Robert A. Millikan in the years 1910-1913. He measured the forces that act on charged oil droplets and confirmed that their electrical charge is always an integral multiple of the elementary charge. In 1923 he received the Nobel Prize for Physics, partly for this work.





