Collection of Solved Problems in Physics

Magnetic Field inside a Toroid

Task number: 1784

Derive the formula for the magnitude of the magnetic field inside a coil that has the shape of a torus whose minor radius is much smaller than the lenght of the central circle. The toroidal coil has N_l turns per unit length and current I flows through it.

• Hint - What is a Toroidal Coil?

  The coil with the shape of a slim toroid is in fact a solenoid (a long slim densely wound coil) whose ends are bent together to form a hollow ring. Asses the magnetic field in the torus from the field in the solenoid, see taks Magnetic Field inside a Solenoid.

• Hint - Ampère’s Law

  In electrostatics, Gauss’ law is used in symmetrical cases to calculate the magnitude of the electric field vector \(\vec{E}\). In a similar way, Ampère’s law is used to calculate the magnitude of the magnetic field vector \(\vec{B}\) in some symmetrical cases.

  Mathematically, Ampère’s law is formulated as:

  \[\oint_l \vec{B}\cdot \,\mathrm{d}\vec{l}=\mu_o I_c,\]

  where I_c stands for the total current flowing through the Ampère’s loop of length l.

• Analysis

  We asses the magnetic field inside the toroid using the formula for the magnetic field in a solenoid because a toroid is in fact a solenoid whose ends are bent together to form a hollow ring. The magnetic field lines inside the toroid are concentric circles. The magnetic field is homogeneous inside the toroid and zero outside the toroid.

  

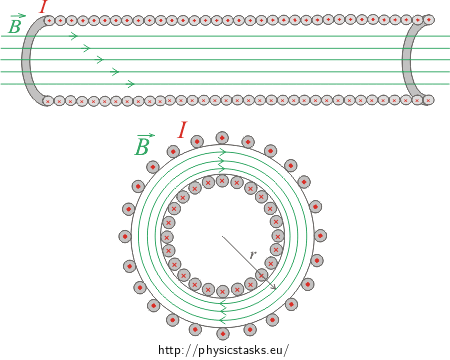
  We asses the direction of the magnetic B-field by the right-hand rule. We chose one circular magnetic field line with radius r for the Ampère’s loop and we go clockwise around it.

• Solution

  We can infer from the shape of the ring-solenoid coil that the magnetic field lines are concentric circles inside the toroid. The magnetic field outside the toroid is zero.

  

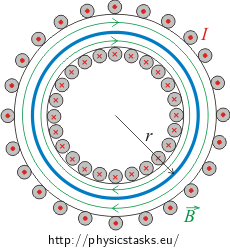
  We determine the magnitude of the magnetic B-field by using Ampère’s law (see the hint):

  \[\int_l \vec{B}\cdot \,\mathrm{d}\vec{l}=\mu_o I_c.\]

  We chose a circle running through the center of the cavity of the torus (the blue line in the figure) for Ampère’s loop. The length of this circle is

  \[l=2\pi r.\]

  The total current flowing through the circle bordered by the Ampère’s loop is

  \[I_c=N_l lI=2\pi rN_l I.\]

  Here we have used that the minor radius of the toroid is mach smaller than the length of its central circle (see the assignment).

  The magnetic fiel vector \(\vec{B}\) is parallel to the vector of the length element \(\mathrm{d}\vec{l}\) all the way around the integration path. Thus we can express the right-hand side of Ampère’s law as

  \[\int_l \vec{B}\cdot \,\mathrm{d}\vec{l}=\int_l B\,\mathrm{d}l=B\int_l\,\mathrm{d}l=B\,2\pi r.\]

  The left-hand and the right-hand sides of the Ampère’s law must be equal and we can express the sought-for magnitude of the magnetic B-field

  \[B2\pi r=2\pi\mu_o rN_l I,\] \[B=\mu_oN_l I.\]

  ---

  Note: The derived formula holds for magnetic field of the toroid in vacuum. If the toroid is filled with a material then the permittivity of vacuum μ_o must be replace by the permittivity of the actual material

  \[\mu =\mu_r\mu_o.\]

• Answer

  We have derived the formula for the magnitude of the magnetic field inside the toroidal coil,

  \[B=\mu_oN_l I.\]

• Direction of the Magnetic Field

  The direction of the magnetic B-field can be determined by using the right-hand rule. If your right hand grabs the toroid with the fingers in the direction of the current in the turns of the coils then the raised thumb of the right hand directs in the direction of the magnetic B-field inside the toroid.