Collection of Solved Problems in Physics

Instantaneous Voltage and Current Values in a Series RLC Circuit

Task number: 1543

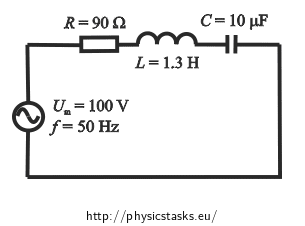
An AC series circuit consists of a resistor with resistance of 90 Ω, a coil with inductance of 1.3 H and a capacitor with capacitance of 10 μF. The circuit is connected to an AC voltage source with amplitude of 100 V and frequency of 50 Hz. Write an equation for instantaneous values of voltage and current in the circuit, if the initial phase of the current is zero.

• Given values

  We write down the quantities and values given in the section Assignment

  Amplitude of the alternating voltage in the circuit	Um = 100 V
  Frequency of the AC power source	f  = 50 Hz
  Resistance of the resistor	R = 90 Ω
  Inductance of the coil	L = 1.3 H
  Capacitance of the capacitor	C = 10 μF
  Initial current phase	φ0i = 0

  Quantities we want to determine:

  Instantaneous current value	i(t) = ? (A)
  Instantaneous voltage value	u(t) = ? (V)

• Hint 1

  The behaviour of alternating voltage and current can be described by a sine function.

  Find the equations describing the instantaneous values of the alternating voltage and the current.

• Hint 2

  When evaluating these equations we need to know the current amplitude I_m and a phase difference φ_0u between the voltage and the current. These we determine by using Ohm's law for alternating current.

  In the task Series RLC Circuit you can find a detailed explanation of the calculation of the current and the phase difference.

• Determining amplitude of current I_m

  We apply Ohm's law for a circuit with alternating current:

  \[I_m=\frac{U_m}{Z}=\frac{U_m}{\sqrt{R^2+\left(X_L-X_C\right)^2}}=\frac{U_m}{\sqrt{R^2+\left(2 \pi f L - \frac{1}{2 \pi f C}\right)^2}} \]

  ---

  We insert the given values:

  \[I_m=\frac{100}{\sqrt{90^2+\left(2 \pi \cdot 50 {\cdot} 1{.}3 - \frac{1}{2 \pi \cdot 50 {\cdot} 10 \cdot 10^{-6}}\right)^2}} \, \mathrm{A} \] \[I_m \,\dot{=}\, 0{.}79 \, \mathrm{A}\]

• Determining phase difference between voltage and current φ_0u

  We use the formula for phase difference expressed by impedance of each element.

  \[ \mathrm{tg\,} \varphi_{0u} = \frac{X_L - X_C}{R}= \frac{\omega L- \frac{1}{ \omega C}}{R}= \frac{2 \pi f L- \frac{1}{ 2 \pi f C}}{R} \] \[\varphi_{0u} = \mathrm{arctg\,}\left(\frac{2 \pi f L- \frac{1}{ 2 \pi f C}}{R}\right)\]

  ---

  Numerical solution:

  \[\varphi_{0u} = \mathrm{arctg\,}\left(\frac{2 \pi f L- \frac{1}{ 2 \pi f C}}{R}\right)= \mathrm{arctg\,}\left(\frac{2\pi \cdot 50 {\cdot} 1.3 - \frac{1}{ 2 \pi \cdot 50 {\cdot} 10 \cdot 10^{-6}}}{90}\right)\] \[\varphi_{0u} \,\dot{=}\, 45 ^{\circ} = \frac{\pi}{4} \]

• Instantaneous values of alternating voltage and current

  Instantaneous value of alternating current:

  The phase difference of the current is zero; the current amplitude I_m has been calculated above.

  \[ i(t)=I_m \, \sin(\omega t + \varphi_{0i})=I_m\, \sin( 2 \pi f t + \varphi_{0i} ) \] \[ i(t)\,\dot{=}\,0.79 \cdot \sin(2 \pi 50 t)\,\mathrm A =0.79 \cdot \sin(100 \pi t)\,\mathrm A\]

   

  Instantaneous value of alternating voltage:

  We know the voltage amplitude U_m and we have determined the phase difference.

  \[ u(t)=U_m \, \sin(\omega t + \varphi_{0u})=U_m \, \sin( 2 \pi f t + \varphi_{0u} ) \] \[u(t)\,\dot{=}\,100 \cdot \sin( 2 \pi 50 t + \frac{\pi}{4} )\,\mathrm V = 100\cdot \sin( 100 \pi t + \frac{\pi}{4} )\,\mathrm V\]

  The time values inserted into the equations are converted into seconds.

• Answer

  The equations for instantaneous values of the voltage and the current in a series RLC circuit with AC have approximately the shape of:

  \[ i(t)=0{.}79 \cdot \sin\left({100 \pi t}\right)\,\mathrm A\] \[u(t)=100 \cdot \sin\left( 100 \pi t + \frac{\pi}{4} \right)\,\mathrm V \]