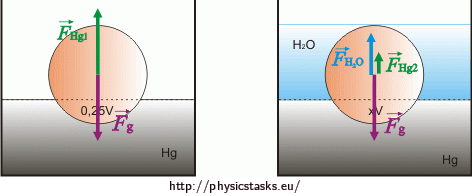
Ball Floating in the Mercury
Task number: 1147
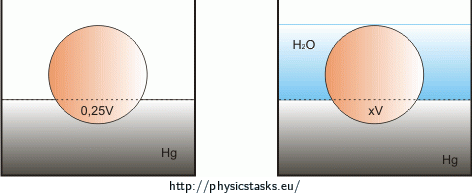
Homogeneous ball is floating in the Mercury that one quarter of its volume is below the surface. Later, on the top of the Mercury is placed appropriate amount of water that whole ball is submerged. Which part of the ball’s volume is submerged in the Mercury in this case?
At first based on your reasoning can you estimate that submerged volume is smaller or bigger than in the first case? Then do the calculations.
Hint 1
Which forces are acting on the ball in both cases? Draw them in the pictures.
Hint 2
Ball is in both cases in the equilibrium. What is happening with the forces action on the ball?
Hint 3
How is calculated a force of gravity acting on the ball, a buoyancy force of the Mercury and a buoyancy force of water?
Hint 4
Formulas for the forces were calculated. Substitute those formulas into (1) and (2) and then find a formula for a variable x
Hint 5
For variable \(x\) was found a formula:
\[x=\frac{\frac{1}{4}\rho_{Hg}-\rho_{H_{2}O}}{\rho_{Hg}-\rho_{H_{2}O}} \]
Find in the physical tables necessary values and calculate numerical value of the \(x\).
Solution
We draw acting forces to the ball in both cases.
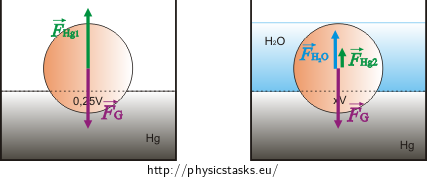
Formula for force of gravity \(F_{g}\) is in both cases:
\[F_{g}=mg\,,\tag{1}\]where \(m\) is ball’s mass and \(g\) is gravitational acceleration.
General formula for buoyancy force \(B\) is:
\[B=V_{disp}\rho_{f}g\,,\]where\(V_{disp}\) is the volume of the submerge part of the body and \(\rho_{f}\) is the desity of the fluid.
In the first case in the formula of the buoyancy force \(B_{Hg_{1}}\) is \(V_{disp}=\frac{1}{4}V\) and\(\rho_{f}=\rho_{Hg}\), where \(V\) is volume of the ball and \(\rho_{Hg}\) is density of the Mercury. Thus:
\[B_{Hg_{1}}=\frac{1}{4}V\rho_{Hg}g\,.\tag{2}\]The second case in the formula of the buoyancy force \(B_{Hg_{2}}\) is \(V_{disp}=xV\) and \(\rho_{f}=\rho_{Hg}\), where \(x\) is volume of the ball submerged in the Mercury. Thus:
\[B_{Hg_{2}}=xV\rho_{Hg}g\,.\tag{3}\]
In the formula of the buoyancy force of the water \(B_{H_{2}O}\) is \(V_{disp}=V-xV\) and \(\rho_{f}=\rho_{H_{2}O}\), Thus:
\[B_{H_{2}O}=(V-xV)\rho_{H_{2}O}g\,.\tag{4}\]
As it is shown on the pictures, in the first case the forces acting on the ball are gravitational force and buoyancy force of the Mercury (buoyancy force of the air is negligible). In the second case is added buoyancy force of the water.
In the first case is the force of gravity acting on the ball equal to the buoyancy force of the Mercury.
\[F_{g}=B_{Hg_{1}}\]
According to the formulas (1) and (2):
\[mg=\frac{1}{4}V\rho_{Hg}g\,.\]
\(g\) is canceled out and \(m\) is used formula \(m=\rho_{b}V\), where \(\rho_{b}\) is the density of the ball.
\[\rho_{b}V=\frac{1}{4}V\rho_{Hg}\]
\(V\) is canceled out, thus:
\[\rho_{b}=\frac{1}{4}\rho_{Hg}.\tag{5}\]
In the second case force of gravity acting on the ball is equal to buoyancy forces of the Mercury and water.
\[F_{g}=B_{Hg_{2}}+B_{H_{2}O}\]
Substituting formulas (1), (3) and (4) into a previous formula:
\[mg=xV\rho_{Hg}g+(V-xV)\rho_{H_{2}O}g\,.\]
\(g\) is canceled out, for \(m\) is used formula \(m=\rho_{b}V\) and \(V\)is factored out the brackets.
\[\rho_{b}V=xV\rho_{Hg}+V(1-x)\rho_{H_{2}O}\]
\(V\) is cancelled out and for \(\rho_{b}\) is used formula (5):
\[\frac{1}{4}\rho_{Hg}=x\rho_{Hg}+(1-x)\rho_{H_{2}O}\]
Brackets are expanded and x is factored out.
\[\frac{1}{4}\rho_{Hg}=x(\rho_{Hg}-\rho_{H_{2}O})+\rho_{H_{2}O}\]
Variable \(x\) is calculated by subtracting \(\rho_{H_{2}O}\) from both sites of the formula and dividing formula by expression \(\rho_{Hg}-\rho_{H_{2}O}\).
\[x=\frac{\frac{1}{4}\rho_{Hg}-\rho_{H_{2}O}}{\rho_{Hg}-\rho_{H_{2}O}} \]
From physical tables:
\[\rho_{Hg}=13 600\mathrm{\frac{kg}{m^3}}\]
\[\rho_{H_{2}O}= 1 000\mathrm{\frac{kg}{m^3}}\]
Substituting numerical values into the formula of \(x\):
\[x=\frac{\frac{1}{4}{\cdot}13600-1000}{13600-1000} \dot=0{,}19\,.\]
Answer
In the second case is submerged in the Mercury ball’s part \(x\). This part is equal to \(x=\frac{\frac{1}{4}\rho_{Hg}-\rho_{H_{2}O}}{\rho_{Hg}-\rho_{H_{2}O}} \dot =\, 0{,}19 \) of the ball’s volume.