A ball in a honey
Task number: 652
Put a steel ball with the mass m = 1g into a jar with honey. Drag force F that affects the box is directly proportional to its speed.
1) Figure out the maximum speed vmax which the ball can reach. .
2) Figure out the progression of the magnitude of the speed v(t) of the ball.

Note: We write only speed instead of the magnitude of the speed hereunder.
Hint 1 – Forces which affect the ball, the motion equation
At first decide which forces affect the ball and if their magnitude is going to change during the motion. Draw a picture.
How is the resultant of these forces going to change?
How is the acceleration and speed of the ball going to change?
Hint 2 – maximum speed
What is the resultant force in the moment when the ball reaches the maximum speed? Write the equation.
Hint 3 – The motion equation, behaviour of the magnitude of the speed v(t)
Look at the picture of the forces which affect the ball and write the motion equation for the ball.
COMPLETE SOLUTION
At first decide which forces affect the ball and if their magnitude is going to change during the motion.
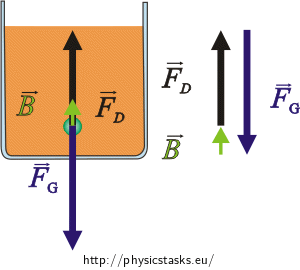
Forces that affect the ball are 3:
\(\vec{F}_{D}\)...drag force
\(\vec{F}_{G}\)...the weight
\(\vec{B}\)...buoyancy force
Expression for the magnitude of previous forces:
FD = kv...grows together with speed
FG = mg...stays constant
B = Vρhg...stays constant
k...constant of the direct proportionality
g...acceleration of gravity with a value of 9.81 m·s-2
V...volume of the ball
ρh...density of honey
How is the magnitude of the resultant force, acceleration and speed of the ball being changed during the motion:
1. The speed of the ball equals zero at the beginning of the motion, and thus drag force equals zero. Due to the fact that the density of steel is bigger than the density of honey, the resultant force is directed downwards as well as the acceleration, and the speed of the ball increases.
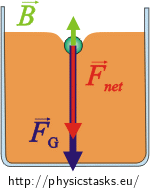
2. As the speed of the ball increases so does the drag force. The magnitude of the resultant force directing downwards decreases as well as the magnitude of the acceleration. The speed of the ball increases but more and more slowly.
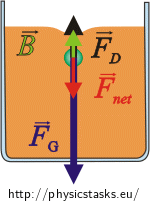
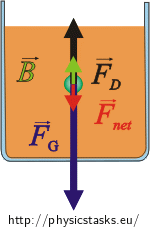
3. In a certain moment the drag force reaches such a magnitude that the forces become equal, acceleration equals zero and the ball continues moving with the constant speed.
In the moment when the ball reaches the maximum speed the resultant force, which affects the ball, equals zero.
The following holds for the forces which affect the ball:
\[\vec{F}_G+\vec{F}_{D}+\vec{B}=0\tag{1}\]
We rewrite the equation (1) to scalar form:
\[F_G-F_{D}-B=0\tag{2}\]
The forces in the equation (2) can be written as:
\[mg-kv_{max}-V\rho_hg=0\tag{3}\]
The maximum speed:
We express the maximum speed vmax from equation (3):
\[v_{max}=\frac{mg-V\rho_hg}{k}\]
We can substitute volume V using equation \(V=\frac{m}{\rho_b}\):
where ρb is the density of the ball, then:
\[v_{max}=\frac{mg-m\frac{\rho_h}{\rho_b}g}{k}\tag{4}\]
Now we determine the behaviour of magnitude of speed of the ball in the process of time. We start from its motion’s equation.
The motion equation for the ball:
\[\vec{F}_G+\vec{F}_{D}+\vec{B}= m\vec{a}\tag{5}\]
We choose the coordinate system so that the y-axis is pointing down in the motion of the ball. We rewrite the equation (5) to scalar form:
\[F_G-F_{D}-B=ma\tag{6}\]
Equation (6) can be written as:
\[mg-kv-V\rho_hg=ma\tag{7}\]
Rewrite acceleration a in the equation (7) as the derivatives of speed with respect to time.
Behaviour of v(t):
\[mg-kv-V\rho_hg=m\frac{dv}{dt}\tag{8}\]
The volume of the ball V can be expressed as follows:
\[V=\frac{m}{\rho_b}\tag{9}\] where
m...mass of the ball
ρb...density of the ball
We substitute equation (9) into equation (8):
\[mg-kv-\frac{m}{\rho_b}\rho_hg=m\frac{dv}{dt}\tag{10}\]
It can be termed for simplicity`s sake:
\[\frac{m}{\rho_b}\rho_h=m\prime\tag{11}\]
We substitute equation (11) into equation (10): :
\[mg-kv-m\prime g=m\frac{dv}{dt}\tag{12}\]
We give the differential equation of the first order with constant coefficients. We solve it by the separation of the variables.
At first divide the equation by m and we rearrange:
\[\frac{m-m\prime}{m}g-\frac{kv}{m}=\frac{dv}{dt}\]
\[-\frac{k}{m}(v-\frac{m-m\prime}{k}g)=\frac{dv}{dt}\]
We separate variables v and t and we integrate the equation:
\[-\frac{k}{m}dt=\frac{dv}{v-\frac{m-m\prime}{k}g} \hspace{20px}/\int\]
\[-\frac{k}{m}t + C=ln|v-\frac{m-m\prime}{k}g|\]
We calculate the equation from the logarithm:
\[e^{(-\frac{k}{m}t+C)} =|v-\frac{m-m\prime}{k}g|\]
\[e^{-\frac{k}{m}t}\cdot e^{C} =|v-\frac{m-m\prime}{k}g|\]
Constant eC can be termed as K:
\[e^{-\frac{k}{m}t}\cdot K=|v-\frac{m-m\prime}{k}g|\tag{13}\]
The expression \(\frac{m-m\prime}{k}g\) is equalled the equation (4) which we have calculated for the maximum speed \(v_{max}=\frac{mg-m\frac{\rho_h}{\rho_b}g}{k}\).
The following holds for the speed v: v ≤ vmax therefore:
\[|v-\frac{m-m\prime}{k}g|=-v+\frac{m-m\prime}{k}g\]
We find out the value of the constant K from the initial value problem. For t = 0 s is v = 0 m·s-1, i. e.:
\[e^0\cdot K=-0+\frac{m-m\prime}{k}g\]
\[K=\frac{m-m\prime}{k}g\]
We substitute for K into equation (13):
\[\frac{m-m^\prime}{k}ge^{-\frac{k}{m}t}\,=\,-v+\frac{m-m^\prime}{k}g\,.\] \[v(t)\,=\,\frac{m-m^\prime}{k}g\left(1-e^{-\frac{k}{m}t}\right)\tag{14}\]COMPLETE ANSWER
The ball can reach the maximum speed \(v_{max}=\frac{mg-m\frac{\rho_h}{\rho_b}g}{k}\).
The progression of the magnitude of the speed v(t) of the ball in relation to the time is given by equation
\[v(t)=\frac{m-m\prime}{k}g(1-e^{-\frac{k}{m}t})\] .



