Motion of a Drop
Task number: 1999
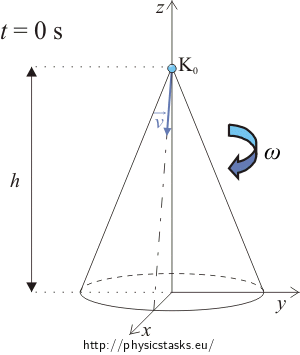
A cone of height h is rotating in a clockwise direction around its axis at constant angular velocity ω. A line on the surface forms an angle α with the axis of the cone. A drop starts trickling down the line on the surface from the vertex of the cone at a constant speed v relative to the cone at time t = 0 s. Describe the behaviour of the position vector of a drop and the behaviour of its velocity in a fixed coordinate system x, y, z chosen so that the z axis is the axis of the cone and the x, y axes lay in its base.
Hint 1: A picture of the situation
Choose the origin of the coordinate system at the centre of the base of the cone and choose the initial position of the drop on the vertex of the cone.
Draw the situation for time t = 0 s and mark the position of the drop.
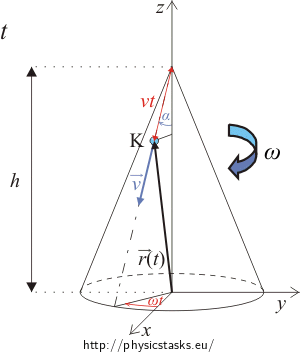
Draw the situation for time t, mark the position of the drop which it has at time t and its position vector.
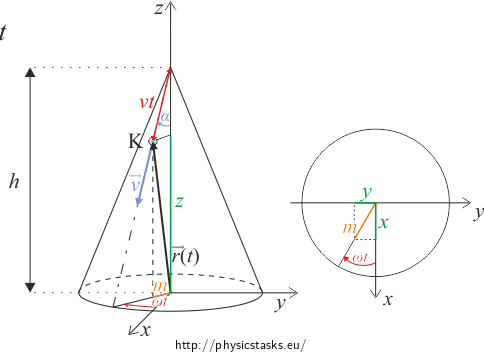
Then mark the position vector projection on the z axis and on the xy plane in the picture.
Hint 2: A behaviour of the position vector of the drop
Look at the pictures in the hint above and form equations for a projection of the position vector of the drop onto the z axis and a projection m of the position vector of the drop onto the xy plane.
Then write equations of the vector projection m onto the x and y axes.
Write the time dependance of the position vector of the drop from those equations.
Hint 3: The behaviour of speed of the drop
Express the components of the velocity vx, vy, vz. How can you get them from the parametric equations?
Then write the behaviour of the speed of the drop.
Complete solution
Figure 1:
Projection of the position vector onto the z axis:
\[z\,=\,h-vt\cos\alpha\,.\]Projection of the position vector onto the xy plane:
\[m\,=\,vt\sin\alpha\,.\]projection m onto x and y axes:
\[x\,=\,m\cos\omega{t}\,=\,vt\sin\alpha\cos\omega{t}\,,\] \[y\,=\,-m\sin\omega{t}\,=\,-vt\sin\alpha\sin\omega{t}\,.\]Time dependence of a position vector of the drop:
\[\vec{r}\left(t\right)\,=\, x\vec{\,i\,} + y\vec{\,j\,} + z\vec{\,k\,}\,,\]
\[\vec{r}\left(t\right)\,=\,vt\sin\alpha\cos\omega{t}\vec{\,i\,}-vt\sin\alpha\sin\omega{t}\vec{\,j\,}+(h-vt\cos\alpha)\vec{\,k\,}\,,\]where \(\vec{\,i\,}\), \(\vec{\,j\,}\), \(\vec{\,k\,}\) are the unit vectors in the direction of coordinate axes.
We get the components of the velocity by deriving the coordinates with respect to time:
\[v_x\,=\,\frac{\mathrm{d}x}{\mathrm{d}t}\,=\, \frac{\mathrm{d}}{\mathrm{d}t}\left(vt\sin\alpha\cos\omega{t}\right)\,=\, v\sin\alpha\cos\omega{t}-v\omega{t}\sin\alpha\sin\omega{t},\] \[v_y\,=\,\frac{\mathrm{d}y}{\mathrm{d}t}\,=\,\frac{\mathrm{d}}{\mathrm{d}t}\left(-vt\sin\alpha\sin\omega{t}\right)\,=\,=\, -v\sin\alpha\sin\omega{t}-v\omega{t}\sin\alpha\cos\omega{t},\] \[v_z\,=\,\frac{\mathrm{d}z}{\mathrm{d}t}\,=\, \frac{\mathrm{d}}{\mathrm{d}t}(h-vt\cos\alpha) \,=\, -v\cos\alpha.\]The behaviour of the velocity of the drop
\[\left|\vec{v}_v\left(t\right)\right|\,=\,\sqrt{v_x^{2}+v_y^{2}+v_z^{2}},\]
\[v_x^{2}\,=\,\left(v\sin\alpha\cos\omega{t}-v\omega{t}\sin\alpha\sin\omega{t}\right)^{2}\,=\] \[\,=\,v^{2}\sin^{2}\alpha\cos^{2}\omega{t}-2v^{2}\omega{t}\sin^{2}\alpha\sin\omega{t}\cos\omega{t}+v^{2}\omega^{2}{t}^{2}\sin^{2}\alpha\sin^{2}\omega{t},\]
\[v_y^{2}\,=\,\left(-v\sin\alpha\sin\omega{t}-v\omega{t}\sin\alpha\cos\omega{t}\right)^{2}\,=\,\] \[\,=\,v^{2}\sin^{2}\alpha\sin^{2}\omega{t}+2v^{2}\omega{t}\sin^{2}\alpha\sin\omega{t}\cos\omega{t}+v^{2}\omega^{2}{t}^{2}\sin^{2}\alpha\cos^{2}\omega{t},\]
\[v_z^{2}\,=\, \left(-v\cos\alpha\right)^{2}\,=\, v^{2}\cos^{2}\alpha,\]
\[v_x^{2}+ v_y^{2}+ v_z^{2}\,=\, v^{2}\sin^{2}\alpha\cos^{2}\omega{t}+v^{2}\sin^{2}\alpha\sin^{2}\omega{t}+\] \[\,+v^{2}\omega^{2}{t}^{2}\sin^{2}\alpha\sin^{2}\omega{t}+ v^{2}\omega^{2}{t}^{2}\sin^{2}\alpha\cos^{2}\omega{t}+v^{2}\cos^{2}\alpha\,=\] \[\,=\,v^{2}\sin^{2}\alpha+v^{2}\omega^{2}{t}^{2}\sin^{2}\alpha+v^{2}\cos^{2}\alpha\,=\] \[\,=\,v^{2}\sin^{2}\alpha+v^{2}\cos^{2}\alpha+v^{2}\omega^{2}{t}^{2}\sin^{2}\alpha\,=\] \[\,=\,v^{2}+v^{2}\omega^{2}{t}^{2}\sin^{2}\alpha,\]
\[\left|\vec{v}_v\left(t\right)\right|\,=\,\sqrt{v_x^{2}+v_y^{2}+v_z^{2}}\,=\,\sqrt{v^{2}+v^{2}\omega^{2}{t}^{2}\sin^{2}\alpha},\]
\[\left|\vec{v}_v\left(t\right)\right|\,=\,\sqrt{v^{2}+\left(vt\omega\sin\alpha\right)^{2}}.\]Answer
The time dependence of the position vector of the drop is:
\[\vec{r}\left(t\right)\,=\,vt\sin\alpha\cos\omega{t}\vec{\,i\,}-vt\sin\alpha\sin\omega{t}\vec{\,j\,}+(h-vt\cos\alpha)\vec{\,k\,},\]where \(\vec{\,i\,}\), \(\vec{\,j\,}\), \(\vec{\,k\,}\) are unit vectors.
The time dependence of the speed of the drop is:
\[\left|\vec{v}_v\left(t\right)\right|\,=\,\sqrt{v_x^{2}+v_y^{2}+v_z^{2}}\,=\,\sqrt{v^{2}+\left(vt\omega\sin\alpha\right)^{2}}.\]