Walking on the boat

Task number: 1148

How far will move a small boat, when a man with 70 kg moves fro stern to prow of the boat. Length of boat is 2.5 m, its mass is 100 kg. Water resistance and tilt of the boat is negligible.

Zápis

m = 70 kg Mass of the man

M = 100 kg Mass of the boat

L = 2.5 m Length of the boat

x = ? Shift of the boat in the horizontal direction
Hint 1
Before we start to think about how to solve the task, describe which external forces are acting on the non-moving system of the boat-man. Which force causes the boat’s movement, when a man starts to move?
Solution Hint 1
If system of the boat-man is considered as one, then the acting external forces are:
- Force of gravity F_g pointing vertically down
- Buoyancy force B pointing vertically up
Resultant of those forces is equal to zero.

Cause of the boat’s movement in the horizontal way is a friction force between a man’s shoes and a surface of the boat; but this force is not an external force.
Description of the solution method
To find the solution is used the fact that the resultant of the external forces acting on the system boat-man is in every moment equal to zero. According the first Newton’s law, the center of gravity is at rest or in uniform motion. In this case is the center of gravity at rest at the beginning and because there is not an external force causing it to accelerate it remain at rest also during the man’s walk. Putting it in the simple way – in point of view of an external observer, position of the center of gravity is conserve. That fact is used to solve this task.
Hint 2
At first is determined the center of gravity before the man started to move. In the picture above appropriately set the coordinate system, prow of the boat is place in the origin. Mark the position of boat’s and man’s center of gravity. Which coordinate of the center of gravity is needed to be solved?
Solution Hint 2
Coordinate system is shown in picture below.

Because the horizontal shift of the boat is solve, only x-coordinate of the center of gravity x_T1 is needed.
Hint 3
Try to remember for a formula for the center of gravity in system of particles and then substitute into it the coordinates from previous step. (During the calculations solid bodies of the boat and man are considered as particles, with mass placed in their centers of gravity.)
Solution Hint 3
For x-coordinate of the center of gravity in the system of n particles is formula:
\[x_{T1}\,=\,\frac{\sum_{i=1}^n{m_ix_i}}{\sum_{i=1}^n{m_i}}\tag{1}\]
In our case masses and a coordinates of the boat and man are substituted into (1):
\[x_{T1}\,=\,\frac{\sum_{i=1}^2{m_ix_i}}{\sum_{i=1}^2{m_i}}\,=\,\frac{M\frac{L}{2}\,+\,mL}{M\,+\,m}\tag{2}\]
Hint 4
Now consider that after a man’s walk from stern to prow a boat move a distance x. In which way is a boat moving? Make a picture describing a new situation and again mark the center of gravity of the boat and man.
Solution Hint 4
In point of view of an external observer after a man’s walk from stern to prow a boat move a distance x to the right – new situation show a picture below:
Hint 5
Like to the first situation make a formula of x-coordinate of the center of gravity, which is referred as x_T2. From the beginning of the task is known that position of the center of gravity remain the same, thus its coordinates are conserved. From this equality expressed unknown distance x.
Solution Hint 5
Coordinate of the center of gravity is again solved by formula (1) – now the formula will look like:
\[x_{T2}\,=\,\frac{\sum_{i=1}^n{m_ix_i'}}{\sum_{i=1}^n{m_i}} \,=\,\frac{mx\,+\,M(x\,+\,\frac{L}{2})}{M\,+\,m}\tag{3}\]
System’s position of the center of gravity remains the same during the walk, thus:
\[x_{T1}\,=\,x_{T2}\]
By using formula (2) and (3):
\[\frac{M\frac{L}{2}\,+\,mL}{M\,+\,m}\,=\,\frac{mx\,+\,M(x\,+\,\frac{L}{2})}{M\,+\,m}\]
Step by step:
\[M\frac{L}{2}\,+\,mL\,=\,mx\,+\,M(x\,+\,\frac{L}{2})\] \[mL\,=\,mx\,+\,Mx\] \[x\,=\,\frac{mL}{M\,+\,m}\]
Numerically:
\[x\,=\,\frac{70{\cdot}2.5}{100\,+\,70}\,\mathrm{m}\,\dot=\,1.03\,\mathrm{m}\]
Boat will move in the horizontal direction approximately 1.03 m.
Solution
If system of the boat-man is considered as one, then the acting external forces are:
- Force of gravity F_g pointing vertically down
- Buoyancy force B pointing vertically up
Resultant of those forces is equal to zero.

Cause of the boat’s movement in the horizontal way is a friction force between a man’s shoes and a surface of the boat; but this force is not an external force.

To find the solution is used the fact that the resultant of the external forces acting on the system boat-man is in every moment equal to zero. According the first Newton’s law, the center of gravity is at rest or in uniform motion. In this case is the center of gravity at rest at the beginning and because there is not an external force causing it to accelerate it remain at rest also during the man’s walk. Putting it in the simple way – in point of view of an external observer, position of the center of gravity is conserve. That fact is used to solve this task.

Coordinate system is shown in picture below.

Because the horizontal shift of the boat is solve, only x-coordinate of the center of gravity x_T1 is needed.

For x-coordinate of the center of gravity in the system of n particles is formula:
\[x_{T1}\,=\,\frac{\sum_{i=1}^n{m_ix_i}}{\sum_{i=1}^n{m_i}}\tag{1}\]
In our case masses and a coordinates of the boat and man are substituted into (1):
\[x_{T1}\,=\,\frac{\sum_{i=1}^2{m_ix_i}}{\sum_{i=1}^2{m_i}}\,=\,\frac{M\frac{L}{2}\,+\,mL}{M\,+\,m}\tag{2}\]
In point of view of an external observer after a man’s walk from stern to prow a boat move a distance x to the right – new situation show a picture below:

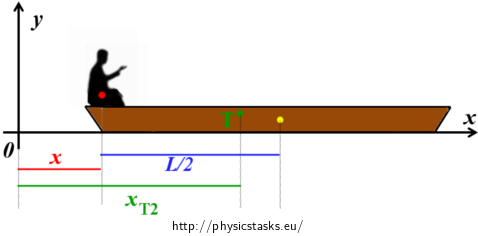
Coordinate of the center of gravity is again solved by formula (1) – now the formula will look like:
\[x_{T2}\,=\,\frac{\sum_{i=1}^n{m_ix_i'}}{\sum_{i=1}^n{m_i}} \,=\,\frac{mx\,+\,M(x\,+\,\frac{L}{2})}{M\,+\,m}\tag{3}\]
System’s position of the center of gravity remains the same during the walk, thus:
\[x_{T1}\,=\,x_{T2}\]
By using formula (2) and (3):
\[\frac{M\frac{L}{2}\,+\,mL}{M\,+\,m}\,=\,\frac{mx\,+\,M(x\,+\,\frac{L}{2})}{M\,+\,m}\]
Step by step:
\[M\frac{L}{2}\,+\,mL\,=\,mx\,+\,M(x\,+\,\frac{L}{2})\] \[mL\,=\,mx\,+\,Mx\] \[x\,=\,\frac{mL}{M\,+\,m}\]
Numerically:
\[x\,=\,\frac{70{\cdot}2.5}{100\,+\,70}\,\mathrm{m}\,\dot=\,1.03\,\mathrm{m}\]
Boat will move in the horizontal direction approximately 1.03 m.
Answer
Boat will move in the horizontal direction approximately o 1.03 m.