Einstein at the platform
Task number: 1515
Massive horizontal platform rotates around a vertical axis and performs \(n_1\) turns per second. In the center of the platform stands a man holding two equal weights each of mass \(m\) in the spread hands. Distance of weights is in this case \(2l_1\). Then man bending hands so distance of the weights is reduced to \(2l_2\). System consisting of the platform, man and the weights then performs \(n_2\) turns per second.
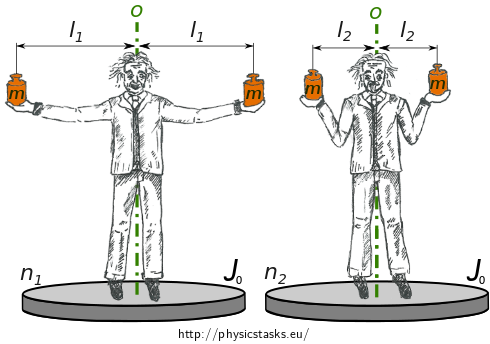
- Determine the moment of inertia of platform.
- Determine work man executes by closing the weights to body.
Don’t consider mass of the man in the platform’s center.
Preparatory guide
Moment of inertiaIf there is a mass point having a mass \(m\) at a distance \(r\) from the axis of rotation, its moment of inertia about this axis is
\[J = mr^2.\]Moment of inertia is an additive quantity. If distances of mass points from the axis are \(r_i\) and their mass are \(m_i\) the moment of inertia of the system of these points around the axis is
\[J = \sum_{i=1}^{n} J_i = \sum_{i=1}^{n} m_i r_i^2.\tag{1}\] Angular momentumAngular momentum theorem says, that temporal change of angular momentum of the system equals resultant moment of external forces acting on system, i.e.
\[\frac{\mathrm{d}\vec{L}}{\mathrm{d}t} = \sum_{i=1}^{n} \vec{M_i ^\mathrm{ex}}.\]If it’s the resultant moment zero, i.e. \(\sum_{i=1}^n \vec{M_i ^\mathrm{ex}} = \vec{0}\), than
\[\frac{\mathrm{d}\vec{L}}{\mathrm{d}t} = 0 \quad \Longrightarrow \quad \vec{L} = \overset{\longrightarrow}{konst.}\tag{2}\]These result is exactly law of conservation of angular momentum.
If there is resultant moment of external forces acting on the system zero, its angular momentum is constant.The angular momentum for system rotating around the axis \(o\) with angular velocity \({\omega}\) and moment of inertia \(J\) is expressed
\[L_o = J \omega \tag{3}\] Energy of rotationKinetic energy of rotation of system rotating around the axis with angular velocity \(\omega\) and moment of inertia \(J\), is
\[E_k = \frac12 J \omega^2.\tag{4}\]Notation
\(n_1\) number of rotates per second (rotation frequency) with spread hands \(n_2\) number of rotates per second (rotation frequency) with bended hands \(l_1\) distance of weights from axis with spread hands \(l_2\) distance of weights from axis with bended hands \(m\) mass of each weight
\(J = \mathrm{?}\) moment of inertia of the platform \(W = \mathrm{?}\) work done by the man bending hands Hint 1 - the law of conservation of angular momentum
We assume that the platform rotates without friction so nothing hinders its movement.What external forces effect system? What is their resultant moment?
Are the requirements of the law of conservation of angular momentum fulfilled in this rotating system? Try to form it.
Hint 2 - work done
The centrifugal force effects the weights at the rotating system. The Einstein has to exert force against it to don’t let weights fly off. During bending hands to body he exerts force along a track, so he did work.
How the work done by man have an impact on the system?
COMPLETE SOLUTION
Moments of gravitational forces around the axis are zero. If we neglect the moments of friction forces in the platform’s bearing and from the air, total moment of external forces is zero. The requirement of the law of conservation of angular momentum (2) is fulfilled.
According to law of conservation of angular momentum is total angular momentum of system with spread hands \(\vec{L}_\mathrm{1}\) is equal total angular momentum of system with bended hands \(\vec{L}_\mathrm{2}\), i.e.
\[\vec{L}_\mathrm{1} = \vec{L}_\mathrm{2}\] Due system rotates around the fixed axis, vector of angular momentum is constant and its size as well, so \[ L_1 = L_2. \] Using equation (3) and expression of the angular velocity using frequencies \(n_1\), \(n_2\) obtain \[ J_1 \omega_1 = J_2 \omega_2, \] \[ J_1 2\pi n_1 = J_2 2\pi n_2. \tag{5}\]Moments of inertia around the axis of system with spread hands (\(J_1\)) and with bended hands (\(J_2\)) according to (1) are
\[J_1 = J_0 + 2ml_1^2,\tag{6}\] \[J_2 = J_0 + 2ml_2^2,\tag{7}\]where \(J_0\) is moment of inertia of the platform and product \(2ml_i^2\) represents moment of inertia of both weights, which we replaced by mass points for simplicity.
By substitution (6) and (7) into (5) we gain the law of conservation of angular momentum in the form
\[\left( J_0 + 2ml_1^2\right)2\pi n_1 = \left( J_0 + 2ml_2^2\right)2\pi n_2,\] we gain sought-after moment of inertia \(J_0\) from this equation using elementary operations \[J_0 = 2m\frac{l_1^2 n_1 - l_2^2 n_2}{n_2 - n_1}.\tag{8}\]
The work done by man have an impact by increase of kinetic energy of the system, i.e.
\[ E_{k_2} = E_{k_1} + W \qquad \Rightarrow \qquad W = E_{k_2} - E_{k_1},\tag{9}\]where \(E_{k_1}\) and \(E_{k_2}\) are kinetic energies of the system with spread hands and bended hands.
We express kinetic energies of the rotation (4) in both situations. We substitute moments of inertia from expressions (6) and (7), express angular velocity using assigned frequencies again
\[E_{\mathrm{k}1} = \frac{1}{2}J_1 \omega_1^2 = 2\pi^2 (J_0 + 2ml_1^2){n_1}^2, \tag{10}\] \[E_{\mathrm{k}2} = \frac{1}{2}J_2 \omega_2^2 = 2\pi^2 (J_0 + 2ml_2^2){n_2}^2. \tag{11}\]By substitution expressions (10) and (11) into expression for work (9) we gain
\[W = E_{k_2} - E_{k_1} = 2\pi^2\left[ (J_0 + 2ml_2^2) n_2^2 - (J_0 + 2ml_1^2)n_1^2\right] = \] \[ = 2\pi^2\left[ J_0 (n_2^2 - n_1^2) + 2m(l_2^2 n_2^2 - l_1^2 n_1^2)\right]. \]By substitution for moment of inertia \(J_0\) from equation (8) we gain final expression
\[ W = 2\pi^2\left[ J_0 (n_2^2 - n_1^2) + 2m(l_2^2 n_2^2 - l_1^2 n_1^2)\right] = \] \[ = 2\pi^2\left[2m\frac{l_1^2 n_1 - l_2^2 n_2}{n_2 - n_1} (n_2^2 - n_1^2) + 2m(l_2^2 n_2^2 - l_1^2 n_1^2)\right]= \] \[ = 4\pi^2 m \left[(l_1^2 n_1 - l_2^2 n_2)(n_2 + n_1) + l_2^2 n_2^2 - l_1^2 n_1^2\right]= \] \[ =4\pi^2 m (l_1^2 - l_2^2) n_1 n_2. \]Answer
- Moment of inertia of the platform is \[J_0 = 2m\frac{l_1^2 n_1 - l_2^2 n_2}{n_2 - n_1}.\]
- Work done by man during bending hands is \[W = 4\pi^2 m \left(l_1^2 - l_2^2\right) n_1 n_2 .\]


