Water Flowing out of a Vessel (or when we pull out a plug)
Task number: 1161
The cylindrical vessel about radius of 90 cm stands on the base of the height of 6 m and is filled with water up the height of 3 m. The vessel is plugged at the bottom about the surface area of 6.3 cm2. Determine:
- With what velocity will the water flow hit the ground when we remove the plug?
- How long will it take before the vessel will be completely empty?
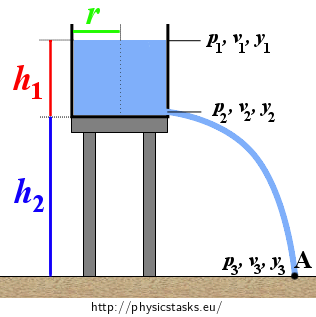
Notation
r = 0.90 m Radius of the cylindrical vessel h1 = 3 m Height of the surface of the water in the vessel h2 = 6 m Height of the base S1 = 6.3 cm2 Surface area of the plug v3 = ? Velocity with which the water falls hits the ground t = ? Time during which the vessel will be completely empty Analysis
We can apply Bernoulli’s principle for the solution of part 1. It is possible to write it either for the situation on the surface and on the ground or in the situation on the surface and at the bottom of the vessel – we have to use our knowledge of the horizontal throw in this case to determine the velocity with which the water hits the ground.
We use the continuity equation in part 2 of this task – the volume of the water in the vessel will drop for a time unit proportionally to the amount of water which will flow out of the vessel. We have to realize that the velocity of the outflow or drop of the water surface isn’t constant because it depends on the height of the surface in the vessel. We will work with drops of very little heights dh in a very short time dt during which we will consider the outlet a constant. We get the total time by the integration of the corresponding equation.
Hint 1 – task a.
We will proceed from the reality that the water from the vessel starts flowing in the moment of the elimination of the plug. Which equation describing the flow could help us with the calculation of the velocity?
Hint 2 – task a
Rewrite Bernoulli’s principle now for:
- the water surface
- point A where the flow of water hits the ground (choose zero level y here)
Which parts from the equation will disappear? Express the required velocity v3 a directly from the remaining parts and calculate it numerically.
Hint 3 – task b.
Proceed from the simple idea that the volume of the water in the vessel is reduced exactly by the amount of the volume which will flow out of the vessel during the time unit.Write the equation continuity for this situation.
Hint 4 – task b.
Think about the velocities. Are they steady in the equation of continuity or not and how to cope with it. Express both velocities.
Hint 5 – task b.
Now substitute relations (8) and (10) into the continuity equation (7) and solve resulting differential equation with separated variables. By integrating within the correct limits you will get total time t during which the vessel will become empty.
Complete solution
Part a.:
Because the water starts flowing after the elimination of the plug, we will use Bernoulli’s principle for the solution to this task. This equation for steady flow has a following shape:
\[p\,+\,y{\varrho}g\,+\,\frac{1}{2}{\varrho}v^2\,=\,c\,\,(c\,=\,constant) \tag{1}\]where p is the external pressure, y is the height above the chosen zero level, ρ is the density of liquid (gas) flow, g is the gravitational acceleration and v is the velocity of the flow. Bernoulli’s principle is a consequence of the law of the conservation of energy and thus the first part on the left can be interpreted as the potential pressure energy, the second as the potential gravitational energy and the third as kinetic energy (all is applied to the volume per unit of the liquid (gas) flow). The sums of these densities of energy equals constant c.
We express the left size of equation (1) for:
- the water surface (quantity with index 1)
- point A (quantity with index 3)
Because both of these left sizes are equal the constant c, they can be put into equality:
\[p_1\,+\,y_1{\varrho}g\,+\,\frac{1}{2}{\varrho}v_1^2\,=\,p_3\,+\,y_3{\varrho}g\,+\,\frac{1}{2}{\varrho}v_3^2\tag{2}\]where ρ is the density of water. Let’s discuss some quantities from relation (2):
- External pressure (affecting in both cases) equals only the atmospheric pressure \[p_1\,=\,p_3\,=\,p_a\tag{3}\] (We are neglecting the difference between the atmospheric pressure of the water surface and point A because its value is smaller by several orders of magnitude than other values in the relation (2).)
- Point A lies in zero height therefore is: \[y_3\,=\,0\tag{4}\]
- Due to the chosen level the surface is in height \[y_1\,=\,h_1\,+\,h_2\tag{5}\]
- The water isn’t almost moving in the moment of releasing of the plug so: \[v_1\,=\,0\tag{6}\]
By substituting relations (3) up to (6) into the equation (2) we will get:
\[p_a\,+\,(h_1\,+\,h_2){\varrho}g\,=\,p_a\,+\,\frac{1}{2}{\varrho}v_3^2\,\Rightarrow\,v_3\,=\,\sqrt{2g(h_1\,+\,h_2)}\]Numerically:
\[v_3\,=\,\sqrt{2{\cdot}9.81{\cdot}(3\,+\,6)}\,\mathrm{m}{\cdot}\mathrm{s^{-1}}\,=\,13.3\,\mathrm{m}{\cdot}\mathrm{s^{-1}}\]
Part b.:
Proceed from the simple idea that the volume of the water in the vessel is reduced exactly by the amount of the volume which will flow out of the vessel during the time unit. This leads directly to the idea of using the equation of continuity in the form:
\[S_1v_1\,=\,S_2v_2\tag{7}\]where S1 is the surface area of the circular base of the vessel, v1 is the velocity of the drop of the surface, S2 is the surface area of the plug and v2 is the velocity of the water which is flowing out of the plughole the plug is removed.
Velocities v1, v2 aren’t constant while the water is flowing out of the vessel, which we can clearly see just having a look at the figure. The lower the surface in the vessel will be the more slowly will the water flow out of the wessel, which will retrospectivly slow down the dropping of the water surface. In the continuity equation we will have to focus on the drop of the water by the infinitesimal element dh during time dt for which the discharge speed v2 will be constant at the given surface height h:
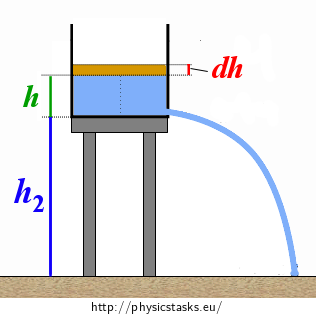
Because the velocity of the drop of the surface v1 is infinitesimally small, we will write for it this:
\[v_1\,=\,-\frac{\mathrm{d}h}{\mathrm{d}t}\tag{8}\]The minus sign appears in expression (8) because the height of the water surface drops and therefore the derivative dh/dt is negative although the velocity v1 is evidently positive. We will determine the discharge speed v2 by using the Bernoulli’s principle which we will write for the water surface in the current height h and for the opening when the plug is removed. We suppose again that the water at the surface doesn’t move. We can neglect the infinitesimal drop of the surface due to the magnitude of the discharge speed. It’s given:
\[p_a\,+\,(h_2\,+\,h){\varrho}g\,=\,p_a\,+\,h_2{\varrho}g\,+\,\frac{1}{2}{\varrho}v_2^2.\tag{9}\]We get from here:
\[v_2\,=\,\sqrt{2gh}\tag{10}\]We get substitution relations (8) and (10) into the continuity equation (7):
\[-\frac{\mathrm{d}h}{\sqrt{h}}\,=\,{\sqrt{2g}}\frac{S_2}{S_1}\mathrm{d}t\]It is a linear differential equation with constants’ coefficients whose variables can be separated:
\[-\frac{\mathrm{d}h}{\sqrt{h}}\,=\,{\sqrt{2g}}\frac{S_2}{S_1}\mathrm{d}t\]We will integrate the whole equation in corresponding limits:
\[-\int_{h_1}^0\frac{\mathrm{d}h}{\sqrt{h}}\,=\,\int_0^t{\sqrt{2g}}\frac{S_2}{S_1}\mathrm{d}t\tag{12}\]For the total time of the vessel emptying we have:
\[2\sqrt{h_1}\,=\,{\sqrt{2g}}\frac{S_2}{S_1}t\,\Rightarrow\,t\,=\,\frac{S_1}{S_2}\sqrt{\frac{2h_1}{g}}\tag{13}\]We substitute the area S1 for area of circle about the radius r and express numerically:
\[t\,=\,\frac{{\pi}{\cdot}0.9^2}{6.3{\cdot}10^{-4}}\sqrt{\frac{2{\cdot}3}{9.81}}\,\mathrm{s}\,\dot=\,3160\,\mathrm{s}\,\dot=\,52.7\,\mathrm{minutes}\]Alternative solution of part a.
We can solve part a. by our knowledge about horizontal throw. The same method is as part b. i.e. the Bernoulli’s principle. We will determine discharge speed v2 from the vessel after removing the plug which is equaled:
\[v_2\,=\,\sqrt{2gh_1}\]This velocity has at the point (where it leaves the vessel) the orthogonal direction on its wall and so it is actually the horizontal component vx of the velocity of a horizontal throw which doesn’t change during the throw:
\[v_x\,=\,v_2\]We will determine the vertical component vy from the kinetic description of a horizontal throw from height h2:
\[v_y\,=\,gt\,=\,g\sqrt{\frac{2h_2}{g}}\,=\,\sqrt{2gh_2}\]It’s given for the total magnitude of the impact velocity of the water flow v3:
\[v\,=\,\sqrt{v_x^2\,+\,v_y^2}\,=\,\sqrt{2g(h1\,+\,h_2)}\]Actually the form is congruent to the expression which we have already acquired in the method mentioned above.
Answer
The impact velocity of the water flow (which will hit the ground after removing the plug) is approximately 13.3 m·s−1. The whole vessel will be empty in 52.7 minutes.


