Hohmann Trajectory

Task number: 1759

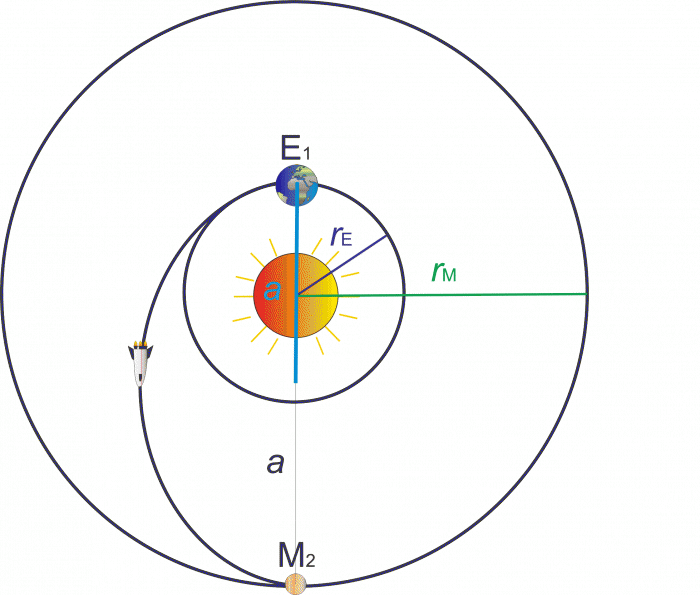
Earth travels around the Sun following a circle trajectory with radius of \(149{.}6{\cdot}10^6 \mathrm{km}\),and the period of its revolution is \(365.25\) days. Mars also travels around the Sun following a circle trajectory and its period of revolution is \(686.96\) days. A spacecraft is sent from Earth to Mars. The most energetically favourable trajectory is so called Hohmann trajectory. It has the shape of a half ellipse, with a starting point on the trajectory of Earth (E₁) and an end point on the trajectory of Mars (M₂), whereas both points must lie on the opposite sides of the Sun.

a) Determine the radius of Mars trajectory, and the magnitude of Mars velocity.

b) Determine the length of the semi-major axis of Hohmann trajectory.

c) Determine the duration of flight of the spacecraft from Earth to Mars following Hohmann trajectory.

d) Determine and plot the position of Mars M₁ at the time of launch of the spacecraft, and the position of Earth E₂ at the time of landing.

Historical note
German scientist Walter Hohmann (1880-1945) contributed to the development of celestial mechanics and the theory of space flight. He discovered an energetically favourable trajectory, with which it would be possible to carry out a flight between planets. This trajectory was named Hohmann trajectory.
Note to figures
In this task, the sizes of objects in the figures are not of real proportions.

Given values

\( r_{\mathrm{E}}=149{.}6{\cdot}10^6 \mathrm{km}\)	radius of trajectory of Earth
\(T_{\mathrm{E}}=365{.}25 \mathrm{days}=31{,}557,600 \mathrm{s}\)	orbital period of Earth around the Sun
\(T_{\mathrm{M}}=686{.}96 \mathrm{days}=59{,}353,344 \mathrm{s}\)	orbital period of Mars around the Sun
\(\mathrm{E}_{1}\)	position of Earth at the time of launch of spacecraft
\(\mathrm{M}_{2}\)	position of Mars at the time of landing of spacecraft
a) \( r_{\mathrm{M}}= ? \mathrm{km}\)	radius of the trajectory of Mars
\(v_{\mathrm{M}}= ? \mathrm{\frac{km}{s}}\)	magnitude of Mars velocity
b) \( a= ? \mathrm{km}\)	length of the semi-major axis of Hohmann trajectory
c) \( t= ? \mathrm{days}\)	time of flight of spacecraft from Earth to Mars following Hohmann trajectory
d) \(M_{\mathrm{1}}\)	position of Mars at the time of launch of spacecraft
e) \(E_{\mathrm{2}}\)	position of Earth at the time of landing of spacecraft

Hint a₁) – radius of Mars trajectory
We use Kepler's third law to determine the radius of Mars trajectory.
Solution of Hint a₁)
According to Kepler's third law it is true that: \[\left(\frac{r_{\mathrm{M}}}{r_{\mathrm{E}}}\right)^3=\left(\frac{T_{\mathrm{M}}}{T_{\mathrm{E}}}\right)^2.\] We multiply both sides of the equation by \(r_{\mathrm{E}}^3\): \[r_{\mathrm{M}}^3=r_{\mathrm{E}}^3\left(\frac{T_{\mathrm{M}}}{T_{\mathrm{E}}}\right)^2.\] Then we take the cube root of both sides of the equation: \[r_{\mathrm{M}}=r_{\mathrm{E}}\sqrt[3]{\left(\frac{T_{\mathrm{M}}}{T_{\mathrm{E}}}\right)^2}.\tag{1}\]

Numerical solution:

\[r_{\mathrm{M}}=149{.}6{\cdot}10^6\sqrt[3] {\left(\frac{686{.}96}{365{.}25}\right)^2} \mathrm{km} \dot= 227{.}94{\cdot}10^6 \mathrm{km}.\]
Hint a₂) – magnitude of Mars velocity
Use the radius of the circle trajectory followed by Mars orbiting the Sun. Its length is easily calculated. To determine the magnitude of Mars velocity, use the known period of revolution.
Solution of Hint a₂)
First, we need to calculate the distance \(s\), which Mars reaches in time \(T_{\mathrm{M}}\). The trajectory of Mars is approximately a circle, therefore it is true that:
\[s=2\pi r_{\mathrm{M}}\tag{2}\]
The magnitude of Mars velocity \(v\) can then be calculated from the relationship:
\[v=\frac{s}{T_{\mathrm{M}}}.\tag{3}\]
We substitute \(s\) from relation (2) into relation (3):
\[v=\frac{2\pi r_{\mathrm{M}}}{T_{\mathrm{M}}}.\]
Then we substitute for \(r_{\mathrm{M}}\) according to (1):
\[v=\frac{2\pi r_{\mathrm{E}}\sqrt[3]{\left(\frac{T_{\mathrm{M}}}{T_{\mathrm{E}}}\right)^2}}{T_{\mathrm{M}}}.\]

Numerical solution:
\[v=\frac{2\pi 149{.}6{\cdot}10^6\sqrt[3] {\left(\frac{686{.}96}{365.25}\right)^2}}{59{,}353,344} \mathrm{\frac{km}{s}} \dot= 24.13\,\mathrm{\frac{km}{s}}.\]
Hint b₁)
Draw a picture of Earth, Mars and the spacecraft trajectories and mark the length of the semi-major axis of Hohmann trajectory.
Solution of Hint b₁)
Hint b₂)
Based on the figure found in the section “Solution of Hint b₁)”, derive a formula for calculating the length of the major axis of Hohmann trajectory.
Solution of Hint b₂)
From the figure we can see that: \[a=\frac{r_{\mathrm{E}}+r_{\mathrm{M}}}{2}.\] For \(r_{\mathrm{M}}\) we can substitute relationship (1): \[ a=\frac{r_{\mathrm{E}}+r_{\mathrm{E}}\sqrt[3]{\left(\frac{T_{\mathrm{M}}}{T_{\mathrm{E}}}\right)^2}}{2}.\] We factor out \(r_{\mathrm{E}}\): \[ a=\frac{r_{\mathrm{E}}\left[1+\sqrt[3]{\left(\frac{T_{\mathrm{M}}}{T_{\mathrm{E}}}\right)^2}\right]}{2}.\tag{4}\]

Numerical solution:

\[ a=\frac{149{.}6{\cdot}10^6\left[1+\sqrt[3]{\left(\frac{686{.}96}{365{.}25}\right)^2}\right]} {2} \mathrm{km} \dot = 188{.}8{\cdot}10^6 \mathrm{km}.\]
Hint c)
To determine the time of flight of the spacecraft from Earth to Mars we use Kepler's third law.
Solution of Hint c)
We denote \(t\) the time of the spacecraft flight. The time it takes the spacecraft to complete the whole Hohmann ellipse is therefore \(2t\).

According to Kepler's third law it applies: \[\left(\frac{2t}{T_{\mathrm{E}}}\right)^2=\left(\frac{a}{r_{\mathrm{E}}}\right)^3.\] We multiply both sides of the equation by \(T_{\mathrm{E}}^2\): \[\left(2t \right)^2 =T_{\mathrm{E}}^2\left(\frac{a}{r_{\mathrm{E}}}\right)^3.\] We take the square root of both sides of the equation: \[ 2t =T_{\mathrm{E}}\sqrt{\left(\frac{a}{r_{\mathrm{E}}}\right)^3}.\] Now we divide both sides of the equation by 2: \[ t =\frac{T_{\mathrm{E}}}{2}\sqrt{\left(\frac{a} {r_{\mathrm{E}}}\right)^3}.\] We substitute relationship (4) for \(a\): \[ t =\frac{T_{\mathrm{E}}}{2}\sqrt{\left(\frac{\frac{r_{\mathrm{E}}\left[1+\sqrt[3]{\left(\frac{T_{\mathrm{M}}}{T_{\mathrm{E}}}\right)^2}\right]}{2}} {r_{\mathrm{E}}}\right)^3}.\] We reduce the fraction and adjust it: \[ t =\frac{T_{\mathrm{E}}}{2} \sqrt { \frac{1}{8}\left[1+\sqrt[3]{\left(\frac{T_{\mathrm{M}}}{T_{\mathrm{E}}}\right)^2}\right] ^3 }.\tag{5}\]

Numerical solution

\[ t =\frac{365{.}25}{2}\sqrt{ \frac{1}{8}\left[1+\sqrt[3]{\left(\frac{686{.}96}{365{.}25}\right)^2}\right]^3} \mathrm{days} \dot= 258{.}86 \mathrm{days} .\]
Hint d₁) – angular shift of Mars
You know the time it takes Mars to orbit once around the Sun and you also know the time of the flight of the spacecraft. Determine the angle by which Mars moves along its trajectory during the time of the spacecraft flight.

To calculate the angle, you can use the rule of three.
Solution of Hint d₁)
One revolution of Mars around the Sun corresponds to angular shift of 2π. We denote \(\alpha_{\mathrm{M}}\) the angular shift of Mars during the time of spacecraft flight.

We write the rule of three: \[T_{\mathrm{M}} ..... 2\pi\] \[t ..... \alpha_{\mathrm{M}}.\] It is a direct proportionality, therefore it applies: \[\frac{t}{T_{\mathrm{M}}}=\frac{\alpha_{\mathrm{M}}}{2\pi}.\] We evaluate \(\alpha_{\mathrm{M}}\) by multiplying both sides of the equation by \(2\pi\): \[\alpha_{\mathrm{M}}=2\pi\frac{t}{T_{\mathrm{M}}}.\] Then we substitute relationship (5) for \(t\): \[\alpha_{\mathrm{M}}=2\pi\frac{\frac{T_{\mathrm{E}}}{2}\sqrt{ \frac{1}{8}\left[1+\sqrt[3]{\left(\frac{T_{\mathrm{M}}}{T_{\mathrm{E}}}\right)^2}\right]^3}}{T_{\mathrm{M}}}.\]

Numerical solution:

The angle \(2\pi\) corresponds to \(360\mathrm{°}\): \[\alpha_{\mathrm{M}}=360\frac{\frac{365{.}25}{2}\sqrt{ \frac{1}{8}\left[1+\sqrt[3]{\left(\frac{686{.}96}{365{.}25}\right)^2}\right]^3}}{686{.}96}\mathrm{°} \dot= 136\mathrm{°}.\]
Hint d₂) – angular sift of Earth
The method used for determining the angular shift of Earth is similar to the one we used for Mars.

Draw the position of Mars at the time of launch of the spacecraft and the position of the Earth at the time of its landing into the picture.
Solution of Hint d₂)
The method used for determining the angular shift of Earth is similar to the one we used for Mars. We denote \(\alpha_{\mathrm{E}}\) the angular shift of Earth.

We write the rule of three: \[T_{\mathrm{E}} ..... 2\pi\] \[t ..... \alpha_{\mathrm{E}}.\] It is a direct proportionality, it therefore applies: \[\frac{t}{T_{\mathrm{E}}}=\frac{\alpha_{\mathrm{E}}}{2\pi}.\] We evaluate \(\alpha_{\mathrm{E}}\) by multiplying both sides of the equation by \(2\pi\): \[\alpha_{\mathrm{E}}=2\pi\frac{t}{T_{\mathrm{E}}}.\] We substitute for \(t\) from (5): \[\alpha_{\mathrm{E}}=2\pi\frac{\frac{T_{\mathrm{E}}}{2}\sqrt{ \frac{1}{8}\left[1+\sqrt[3]{\left(\frac{T_{\mathrm{M}}}{T_{\mathrm{E}}}\right)^2}\right]^3}}{T_{\mathrm{E}}}.\] We reduce the fraction and adjust it: \[\alpha_{\mathrm{E}}=\pi \sqrt{ \frac{1}{8}\left[1+\sqrt[3]{\left(\frac{T_{\mathrm{M}}}{T_{\mathrm{E}}}\right)^2}\right]^3}.\]

Numerical solution

The angle \(\pi\) corresponds to \(180\mathrm{°}.\) \[\alpha_{\mathrm{E}}=180\sqrt{ \frac{1}{8}\left[1+\sqrt[3]{\left(\frac{686{.}96}{365{.}25}\right)^2}\right]^3}\mathrm{°} \dot= 255\mathrm{°}.\]

We draw the position of Mars at the time of launch of the spacecraft and the position of Earth at the time of its landing into the picture.
Overall solution
a) The radius of Mars trajectory and the magnitude of its velocity

According to Kepler's third law it is true that: \[\left(\frac{r_{\mathrm{M}}}{r_{\mathrm{E}}}\right)^3=\left(\frac{T_{\mathrm{M}}}{T_{\mathrm{E}}}\right)^2.\] We multiply both sides of the equation by \(r_{\mathrm{E}}^3\): \[r_{\mathrm{M}}^3=r_{\mathrm{E}}^3\left(\frac{T_{\mathrm{M}}}{T_{\mathrm{E}}}\right)^2.\] Then we take the cube root of both sides of the equation: \[r_{\mathrm{M}}=r_{\mathrm{E}}\sqrt[3]{\left(\frac{T_{\mathrm{M}}}{T_{\mathrm{E}}}\right)^2}.\tag{1}\]

Mars velocity \(v\) is calculated according to the relationship: \[v=\frac{s}{T_{\mathrm{M}}},\tag{2}\] where \(s\) is the distance which Mars reaches in time \(T_{\mathrm{M}}\).

First, we need to calculate the distance \(s\), which Mars reaches it time \(T_{\mathrm{M}}\). The trajectory of Mars is approximately a circle, it therefore applies: \[s=2\pi r_{\mathrm{M}}.\tag{3}\] In equation (2) we substitute \(s\) from equation (3): \[v=\frac{2\pi r_{\mathrm{M}}}{T_{\mathrm{M}}}.\] Then we substitute \(r_{\mathrm{M}}\) according to (1): \[v=\frac{2\pi r_{\mathrm{E}}\sqrt[3]{\left(\frac{T_{\mathrm{M}}}{T_{\mathrm{E}}}\right)^2}}{T_{\mathrm{M}}}.\]

Numerical solution

\[r_{\mathrm{M}}=149{.}6{\cdot}10^6\sqrt[3] {\left(\frac{686{.}96}{365.25}\right)^2} \mathrm{km} \dot= 227{.}94{\cdot}10^6 \mathrm{km}.\]

\[v=\frac{2\pi 149{.}6{\cdot}10^6\sqrt[3] {\left(\frac{686{.}96}{365.25}\right)^2}}{59{,}353,344} \mathrm{\frac{km}{s}} \dot= 24.13 \mathrm{\frac{km}{s}}.\]

b) The length of the semi-major axis of Hohmann trajectory

We draw a picture of trajectory of Earth, Mars and the spacecraft and mark the major axis of Hohmann trajectory.

From the figure we can see that it applies: \[a=\frac{r_{\mathrm{E}}+r_{\mathrm{M}}}{2}.\] We substitute \(r_{\mathrm{M}}\) from equation (1): \[ a=\frac{r_{\mathrm{E}}+r_{\mathrm{E}}\sqrt[3]{\left(\frac{T_{\mathrm{M}}}{T_{\mathrm{E}}}\right)^2}}{2}.\] We factor out \(r_{\mathrm{E}}\): \[ a=\frac{r_{\mathrm{E}}\left[1+\sqrt[3]{\left(\frac{T_{\mathrm{M}}}{T_{\mathrm{E}}}\right)^2}\right]}{2}.\tag{4}\]

Numerical solution

\[ a=\frac{149{.}6{\cdot}10^6\left[1+\sqrt[3]{\left(\frac{686{.}96}{365.25}\right)^2}\right]} {2} \mathrm{km} \dot = 188{.}8{\cdot}10^6 \mathrm{km}.\]

c) The time of spacecraft flight from Earth to Mars following Hohmann trajectory

We denote \(t\) the time of the spacecraft flight. The time it takes the spacecraft to complete the whole Hohmann ellipse is therefore \(2t\).

According to Kepler's third law it applies: \[\left(\frac{2t}{T_{\mathrm{E}}}\right)^2=\left(\frac{a}{r_{\mathrm{E}}}\right)^3.\] We multiply both sides of the equation by \(T_{\mathrm{E}}^2\): \[\left(2t \right)^2 =T_{\mathrm{E}}^2\left(\frac{a}{r_{\mathrm{E}}}\right)^3.\] We take the square root of both sides of the equation: \[ 2t =T_{\mathrm{E}}\sqrt{\left(\frac{a}{r_{\mathrm{E}}}\right)^3}.\] Now we divide both sides of the equation by 2: \[ t =\frac{T_{\mathrm{E}}}{2}\sqrt{\left(\frac{a} {r_{\mathrm{E}}}\right)^3}.\] We substitute for \(a\) from relationship (4): \[ t =\frac{T_{\mathrm{E}}}{2}\sqrt{\left(\frac{\frac{r_{\mathrm{E}}\left[1+\sqrt[3]{\left(\frac{T_{\mathrm{M}}}{T_{\mathrm{E}}}\right)^2}\right]}{2}} {r_{\mathrm{E}}}\right)^3}.\] We reduce the fraction and adjust it: \[ t =\frac{T_{\mathrm{E}}}{2} \sqrt { \frac{1}{8}\left[1+\sqrt[3]{\left(\frac{T_{\mathrm{M}}}{T_{\mathrm{E}}}\right)^2}\right]^3}.\tag{5}\]

Numerical solution:

\[ t =\frac{365{.}25}{2}\sqrt{ \frac{1}{8}\left[1+\sqrt[3]{\left(\frac{686{.}96}{365{.}25}\right)^2}\right]^3} \mathrm{days} \dot= 258{.}86 \mathrm{days} .\]

d) The position of Mars M₁ at the time of launch of the spacecraft

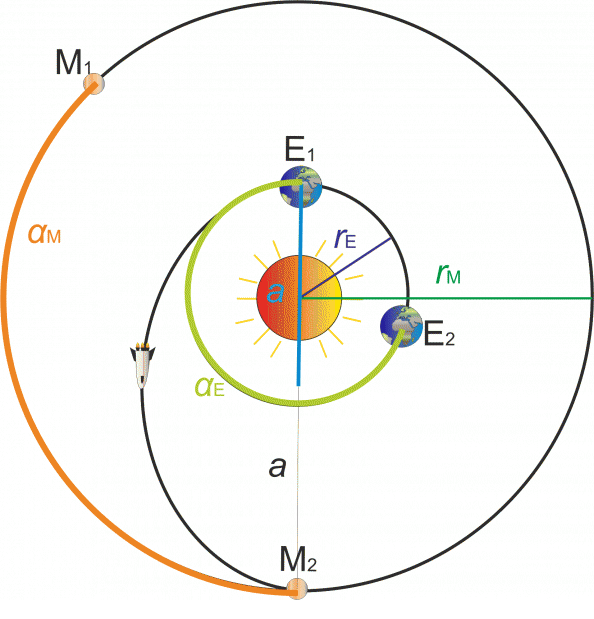
We determine the angular shift \(\alpha_{\mathrm{M}}\) by which Mars has moved during the time of the spacecraft flight along its trajectory.

We write the rule of three: \[T_{\mathrm{M}} ..... 2\pi\] \[t ..... \alpha_{\mathrm{M}}.\] It is a direct proportionality, therefore it applies: \[\frac{t}{T_{\mathrm{M}}}=\frac{\alpha_{\mathrm{M}}}{2\pi}.\] We evaluate \(\alpha_{\mathrm{M}}\) by multiplying both sides of the equation by \(2\pi\): \[\alpha_{\mathrm{M}}=2\pi\frac{t}{T_{\mathrm{M}}}.\] Then we substitute relationship (5) for \(t\): \[\alpha_{\mathrm{M}}=2\pi\frac{ \frac{T_{\mathrm{E}}}{2} \sqrt { \frac{1}{8}\left[1+\sqrt[3]{\left(\frac{T_{\mathrm{M}}}{T_{\mathrm{E}}}\right)^2}\right] ^3 }}{T_{\mathrm{M}}}.\]

Numerical soplution:

The angle \(2\pi\) corresponds to \(360\mathrm{°}.\) \[\alpha_{\mathrm{M}}=360\frac{\frac{365{.}25}{2}\sqrt{ \frac{1}{8}\left[1+\sqrt[3]{\left(\frac{686{.}96}{365{.}25}\right)^2}\right]^3}}{686{.}96}\mathrm{°} \dot= 136\mathrm{°}.\]

The position of Earth E₂ at the time of landing of the spacecraft

We determine the angular shift \(\alpha_{\mathrm{E}}\) by which Earth has moved during the time of the spacecraft flight along its trajectory.

We write the rule of three: \[T_{\mathrm{E}} ..... 2\pi\] \[t ..... \alpha_{\mathrm{E}}.\] It is a direct proportionality, it therefore applies: \[\frac{t}{T_{\mathrm{E}}}=\frac{\alpha_{\mathrm{E}}}{2\pi}.\] We evaluate \(\alpha_{\mathrm{E}}\) by multiplying both sides of the equation by \(2\pi\): \[\alpha_{\mathrm{E}}=2\pi\frac{t}{T_{\mathrm{E}}}.\] We substitute for \(t\) from (5): \[\alpha_{\mathrm{E}}=2\pi\frac{ \frac{T_{\mathrm{E}}}{2} \sqrt { \frac{1}{8}\left[1+\sqrt[3]{\left(\frac{T_{\mathrm{M}}}{T_{\mathrm{E}}}\right)^2}\right] ^3 }}{T_{\mathrm{E}}}.\] We reduce the fraction and adjust it: \[\alpha_{\mathrm{E}}=\pi \sqrt { \frac{1}{8}\left[1+\sqrt[3]{\left(\frac{T_{\mathrm{M}}}{T_{\mathrm{E}}}\right)^2}\right] ^3 }.\]

Numerical solutions:

The angle \(\pi\) corresponds to \(180\mathrm{°}.\) \[\alpha_{\mathrm{E}}=180\sqrt{ \frac{1}{8}\left[1+\sqrt[3]{\left(\frac{686{.}96}{365{.}25}\right)^2}\right]^3}\mathrm{°} \dot= 255\mathrm{°}.\]

Into the picture, we draw the position of Mars M₁ at the time of launch of the spacecraft and the position of Earth E₂ at the time of landing.
Answer
a) The radius of the trajectory of Mars is equal to: \(r_{\mathrm{M}}=r_{\mathrm{E}}\sqrt[3]{\left(\frac{T_{\mathrm{M}}}{T_{\mathrm{}E}}\right)^2}\) and the magnitude of its velocity is: \(v=\frac{2\pi r_{\mathrm{E}}\sqrt[3]{\left(\frac{T_{\mathrm{M}}}{T_{\mathrm{E}}}\right)^2}}{T_{\mathrm{M}}}\).

For given values we obtain: \(r_{\mathrm{M}}=227{.}94{\cdot}10^6 \mathrm{km}\) and \(v\,\dot=\,24.13 \mathrm{\frac{km}{s}}\).

b) The length of the semi-major axis of Hohmann trajectory is equal to: \( a=\frac{r_{\mathrm{E}}\left[1+\sqrt[3]{\left(\frac{T_{\mathrm{M}}}{T_{\mathrm{E}}}\right)^2}\right]}{2}\).

For given values we obtain: \( a \dot = 188{.}8{\cdot}10^6 \mathrm{km}\).

c) The duration of the spacecraft flight from Earth to Mars following Hohmann trajectory is equal to: \( t =\frac{T_{\mathrm{E}}}{2} \sqrt { \frac{1}{8}\left[1+\sqrt[3]{\left(\frac{T_{\mathrm{M}}}{T_{\mathrm{E}}}\right)^2}\right] ^3 }\).

For given values we obtain: \( t \dot= 258{.}86 \mathrm{days} .\)

d) The angular shift of Mars during the time of spacecraft flight is \(\alpha_{\mathrm{M}}=2\pi\frac{ \frac{T_{\mathrm{E}}}{2} \sqrt {\frac{1}{8}\left[1+\sqrt[3]{\left(\frac{T_{\mathrm{M}}}{T_{\mathrm{E}}}\right)^2}\right]^3}}{T_{\mathrm{M}}}\).

For given values we obtain: \(\alpha_{\mathrm{M}} \dot= 136\mathrm{°}\).

The angular shift of Earth during the time of spacecraft flight is: \(\alpha_{\mathrm{E}}=\pi\sqrt{ \frac{1}{8}\left[1+\sqrt[3]{\left(\frac{T_{\mathrm{M}}}{T_{\mathrm{E}}}\right)^2}\right]^3}\) .

For given values we obtain: \(\alpha_{\mathrm{E}} \dot= 255\mathrm{°}\).