Bicyclist going uphill
Task number: 280
A bicyclist is going up a 5% slope by a uniform speed of 27 km·h-1. The magnitude of the air resistance force is given by Fres = kv2 where the numerical value of {k} = 0.3 if the unit of the speed is m·s-1 and the unit of the resistance force is the newton (N). The mass of the bicyclist including the bike is 70 kg. Do not consider the rolling resistance.
What forward force exerted on the bike by the road is needed to make the bicyclist move with constant speed?
How much work does the bicyclist do when riding a distance of 1200 m? What is the power of the bicyclist during the ride? Assume there is no loss of mechanical energy.
Hint 1 – acting forces
Draw a figure (a free body diagram) with all forces acting on the bicyclist and the bike. What can you tell about the net force acting on the bicyclist riding with constant speed?
Hint 2 – the work and the power of the bicyclist
Assuming there is no loss of mechanical energy the bicyclist’s work is equal to the work done by the forward force exerted on the bike by the road. This forward force is constant during the ride. What work does it do along the 1200-m ride?
How can we calculate the power if the force and the speed are given?
Numerical values
It is given:
\[m=70\, \mathrm{kg}\] \[\sin\alpha=5\%=0.05\] \[k=0.3\,\mathrm{kgm^{-1}}\] \[v=27\, \mathrm{km h^{-1}}=7.5\,\mathrm{m s^{-1}}\]We are looking for:
\[F=?\] \[W=? \] \[P=?\] \[F=F_{odp}+F_{g}\sin\alpha\] \[F=kv^{2}+mg\sin\alpha\] \[F=(0.3{\cdot}7.5^{2}+70{\cdot}9.81{\cdot}0.05)\,\mathrm{N}\] \[F=51.2\, \mathrm{N}\] \[W=Fs\] \[W=51.2{\cdot}1200\,\mathrm{J}\] \[W=61440\, \mathrm{J}\,\dot=61.4\ \mathrm{kJ}\] \[P=(F_{odp}+F_g\sin\alpha)v\] \[P=(kv^2+mg\sin\alpha)v\] \[P=(0.3{\cdot}7.5^{2}+70{\cdot}9.81{\cdot}0.05)\cdot7.5\,\mathrm{W}\] \[P=51.2{\cdot}7.5\,\mathrm{W}\] \[P=384\, \mathrm{W}\]Answer
The magnitude of the forward force exerted on the bike by the road is \(F=kv^2+mg\sin\alpha=51.2\, \mathrm{N}\).
The work done by the bicyclist when riding a distance of 1200 m is \(W=(kv^2+mg\sin\alpha)s\,\dot=61.4\ \mathrm{kJ}\).
The power of the bicyclist during the uphill ride is \(P=(kv^2+mg\sin\alpha)v=384\, \mathrm{W}\).
Complete solution
Determination of the force:
To simplify the figure we consider the bicyclist and the bike as one body. We draw in the figure all forces acting on this body.
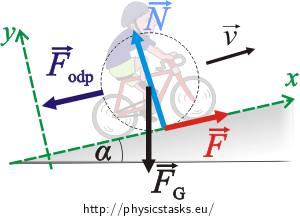
\(\vec{F_g}\)...... the weight
\(\vec{N}\)...... the normal force exerted on the bike by the road
\(\vec{F_{odp}}\)...... the air resistance force
\(\vec{F}\)...... the unknown forward force exerted on the bike by the road
The net force acting on the bicyclist must be zero when riding with constant speed along a straight line, thus:
\[\vec{F_g}+\vec{F_{odp}}+\vec{N}+\vec{F}=0\]We choose a frame of reference as in the figure and write the x- and y-components of the net force
\[x:\qquad -F_g\sin\alpha-F_{odp}+F=0\tag{1}\] \[y:\qquad N-F_g\cos\alpha=0\]The unknown force is obtained from the equation (1):
\[F=F_g\sin\alpha+F_{odp}=mg\sin\alpha+kv^2\tag{2}\]We determine “sin alpha” from the given slope. The 5% slope means that the road rises up by 5 m along the distance of 100 m (see the figure below)
\[\sin\alpha=\frac{5}{100}=0{,}05\]\[F=kv^2+mg\sin\alpha\tag{2}\] \[F_{c}=0.3{\cdot}7.5^{2}+70{\cdot}9.81{\cdot}0.05\,\mathrm{N}\] \[F_{c}=51.2\, \mathrm{N}\]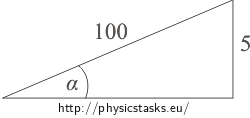
Determination of the work:
The forward force exerted on the bike by the road is constant and acts in the direction of the bicyclist’s motion. Thus the work can be calculated from:
\[W=Fs\]W.... the bicyclist’s work
F...... the forward force exerted on the bike by the road
s...... the distance the bicyclist rides
We substitute the forward force from the equation (2)
\[W=(F_{odp}+F_g\alpha)s\] \[W=(kv^2+mg\sin\alpha)s\] \[W=(0.3{\cdot}7.5^{2}+70{\cdot}9.81{\cdot}0.05)\cdot1200\,\mathrm{J}\] \[W=51.2{\cdot}1200\,\mathrm{J}\] \[W=61440\, J\,\dot=61.4\ \mathrm{kJ}\]Determination of the power:
The power is given by:
\[P=\frac{dW}{dt}=\frac {dF\cdot s}{dt}=F\cdot\frac {ds}{dt}=F\cdot v\]P....... the bicyclist’s power
F........ the forward force exerted on the bike by the road
v........ the speed of the bicyclist
Once again we substitute the forward force from the equation (2):
\[P=(F_{odp}+F_g\sin\alpha)\cdot v\] \[P=(kv^2+mg\sin\alpha)v\] \[P=(0.3{\cdot}7.5^{2}+70{\cdot}9.81{\cdot}0.05)\cdot7.5\,\mathrm{W}\] \[P=51.2{\cdot}7.5\,\mathrm{W}\] \[P=384\, \mathrm{W}\]Answer:
The magnitude of the forward force exerted on the bike by the road is \(F=51.2\, \mathrm{N}\).
The work done by the bicyclist when riding a distance of 1200 m is \(W\,\dot=61.4\ \mathrm{kJ}\).
The power of the bicyclist during the uphill ride is \(P=384\, \mathrm{W}\).




