A Rod Leaning on a Step
Task number: 2228
Notation
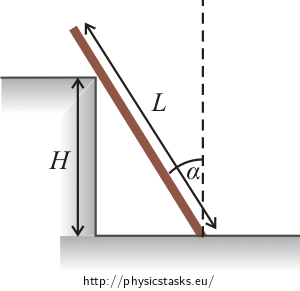
L length of the rod m mass of the rod H height of the step α angle between the rod and the vertical F = ? magnitude of the friction force between the rod and the floor ? magnitude and direction of the other forces exerted by the step and the floor on the rod Hint 1
Which forces are acting on the rod? Draw them in the picture.Hint 2
What applies to the forces and moment of force if the rod is in equilibrium?Hint 3
Write down the conditions of equilibrium and rewrite them using scalars.
Hint 4
First, find distance R, and then express the desired forces from equations (1), (2) and (3).
Overall Solution
First, draw the forces acting on the rod.
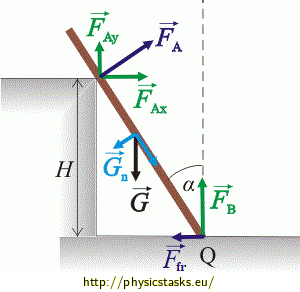
Rod is experiencing weight \(\vec{G} = m \vec{g}\) in its centre of gravity.
On the one hand, floor is pushing the rod vertically upwards with force \(\vec{F}_B\), and on the other hand it is also acting on the rod with friction force \(\vec{F}_{fr}\) directed to the left, so that the rod does not slide. The step is exerting force \(\vec{F}_A\) perpendicular to the rod.
Since the forces acting on the rod keep it in equilibrium, the resultant force on the rod must be zero and the resultant moment of force is zero as well (with respect to any point).
The resultant force is zero:
\[\vec{F}_{A}+\vec{F}_{B}+\vec{G}+\vec{F}_{fr} = \vec{0}\,.\]We choose the common coordinate system (x is positive to the right, y is positive upwards) and rewrite the equation using scalars
\[ x:\hspace{50px} F_{Ax} = F_{fr}\,,\] \[y:\hspace{10px} F_{Ay}+F_B = G\,.\]For the components of force \(\vec{F}_A\) holds:
\[F_{Ax} = F_A \cos \alpha\,,\] \[F_{Ay} = F_A \sin \alpha\,.\]Thus:
\[ F_A \cos \alpha = F_{fr}\,,\tag{1}\] \[ F_A \sin \alpha + F_B = G\,.\tag{2}\]The resultant moment of force is zero with respect to any point:
\[\vec{M}_{G}+\vec{M}_{A}+\vec{M}_{B}+\vec{M}_{fr} = \vec{0}\,.\]Let's also recall the formula for the moment of force \(\vec{F}\) with respect to point O:
\[\vec{M} = \vec{r} \times \vec{F}\,.\]For the magnitude of the moment it holds true: \(M = rF\sin \varphi\), where \(\varphi\) is the angle between vector \(\vec{r}\) and \(\vec{F}\).
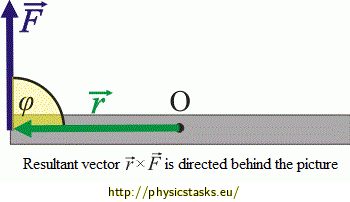
Direction of the moment of force is perpendicular to the plane containing vector \(\vec{r}\) and \(\vec{F}\). Its orientation can be determined by the right-hand rule: if we curl the fingers in the direction from \(\vec{r}\) to \(\vec{F}\), the out-stretched thumb will show the direction of vector \(\vec{M}\).
We are going to determine the moment of force with respect to point Q, at which the rod is touching the floor. This way we nullify the moment of force acting in this point (\(\vec{r}_{fr} = \vec{0}\) and \(\vec{r}_B = \vec{0}\)).
The adjusted equation is:
\[ \vec{M}_G + \vec{M}_A = \vec{0}\,.\]We choose a clockwise direction of rotation as negative, and thus, we consider the moment of force directed :“behind the paper:” to be negative. Then
\[ M_G - M_A = 0\,.\]For the magnitude of the moment we get:
\[ \frac{L}{2} G \sin \alpha - RF_A = 0\,,\tag{3}\]where R is the distance between point Q and point of force \(\vec{F}_A\).
Distance between the point at which force FA is applied and point Q can be calculated using a triangle whose sides are formed by the floor, rod and side of the step. Angle between the step and rod is α, so
\[R=\frac{H}{\cos \alpha}\,.\]The rest is simple mathematics. From (3) we obtain:
\[F_A=GL \frac{\sin \alpha} {2R}\,.\]We substitute R:
\[F_A=GL \frac{\sin \alpha \cos \alpha} {2H}\,.\]From (1):
\[F_{fr}= F_A \cos \alpha = GL \frac{\sin \alpha \cos^2\alpha}{2H}\,.\]Now, only force FB is left, and we can determine it by substituting FA in (2):
\[F_B=G -GL \frac{\sin^2\alpha \cos \alpha}{2H}\,.\]The result can also be adjusted as follows:
\[\sin(2\alpha)=2 \sin \alpha \cos \alpha\,,\] \[F_A=GL \frac{\sin 2\alpha} {4H}\,,\] \[F_B=G-GL \frac{\sin 2\alpha \sin \alpha} {4H}\,,\] \[F_{fr}=GL \frac{\sin 2\alpha \cos \alpha} {4H}\,.\]Answer
Magnitudes of the forces acting on the rod are as follows:
\[F_A=GL \frac{\sin 2\alpha} {4H}\,,\] \[F_B=G-GL \frac{\sin 2\alpha \sin \alpha} {4H}\,.\] \[F_{fr}=GL \frac{\sin 2\alpha \cos \alpha} {4H}\,.\]Direction of these forces are shown in the figure.

Similar Problem
Solved? Try a similar task A leaning ladder.




